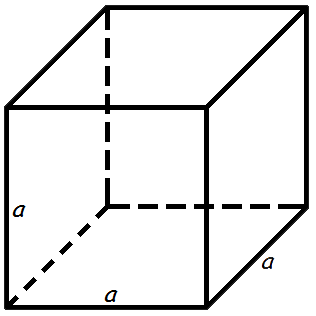
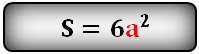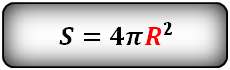Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
- Площадь прямоугольного параллелепипеда
- Площадь цилиндра
- Площадь конуса
- Площадь шара
- Все формулы для площадей полной и боковой поверхности тел
- 1. Площадь полной поверхности куба
- 2. Найти площадь поверхности прямоугольного параллелепипеда
- 3. Найти площадь поверхности шара, сферы
- 4. Найти площадь боковой и полной поверхности цилиндра
- 5. Площадь поверхности прямого, кругового конуса
- 5.5.6 Площадь поверхности конуса, цилиндра, сферы
- Формулы площади поверхности тел
- Формула площади поверхности призмы
- Формула площади поверхности куба
- Формула площади поверхности пирамиды
- Формула площади поверхности цилиндра
- Формула площади поверхности конуса
- Формула площади поверхности шара (сферы)
- Формула площади поверхности сферического сегмента
- Формула площади поверхности шарового сегмента
- Как найти площадь полной поверхности призмы пирамиды цилиндра конуса
- Объем призмы
- Объем параллелепипеда
- Объем прямоугольного параллелепипеда
- Объем пирамиды
- Объем правильного тетраэдра
- Объем цилиндра
- Объем конуса
- Объем шара
- Площадь куба
- Площадь прямоугольного параллелепипеда
- Площадь цилиндра
Видео:Площадь поверхности призмы. 11 класс.Скачать

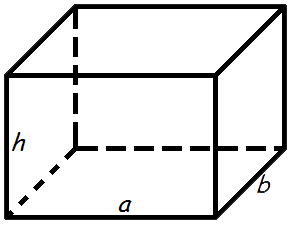
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда:
Видео:Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

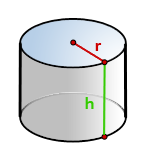
Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
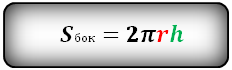
Формула для вычисления площади боковой поверхности цилиндра:
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра:
Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

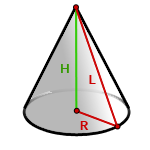
Площадь конуса
Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число π .
Формула площади боковой поверхности конуса:
Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.
Формула площади полной поверхности конуса:
Видео:Видеоурок по математике "Цилиндр"Скачать

Площадь шара
Площадь поверхности шара равна четырем его радиусам в квадрате умноженным на число π .
Площадь поверхности шара равна квадрату его диаметра умноженного на число π .
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Читайте также: Высота цилиндра формула через объем
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Все формулы для площадей полной и боковой поверхности тел
Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

1. Площадь полной поверхности куба
a — сторона куба
Формула площади поверхности куба,(S):
Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

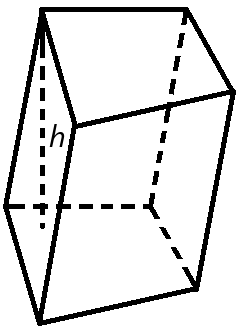
2. Найти площадь поверхности прямоугольного параллелепипеда
a , b , c — стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):
Видео:Площадь полной поверхности призмыСкачать

3. Найти площадь поверхности шара, сферы
R — радиус сферы
Формула площади поверхности шара (S):
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

4. Найти площадь боковой и полной поверхности цилиндра
r — радиус основания
h — высота цилиндра
Формула площади боковой поверхности цилиндра, (S бок ):
Формула площади всей поверхности цилиндра, (S):
Видео:Объемы и площади куба, шара, конуса, призмы и цилиндраСкачать

5. Площадь поверхности прямого, кругового конуса
R — радиус основания конуса
L — образующая конуса
Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S бок ):
Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S бок ):
Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):
Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):
Видео:Площадь поверхности призмы. Практическая часть. 11 класс.Скачать

5.5.6 Площадь поверхности конуса, цилиндра, сферы
Видеоурок: Объем и площадь поверхности тел вращения
Лекция: Площадь поверхности конуса, цилиндра, сферы
Поверхность цилиндра
Давайте вспомним, из чего состоит цилиндр – из боковой поверхности и двух оснований. Чтобы найти площадь всей боковой поверхности, следует найти площади каждой отдельной поверхности. Это значит, что для получения площади двух оснований (окружностей), следует воспользоваться формулой:
Двойка в формуле появилось из-за того, что у цилиндра два одинаковых основания. Поэтому вместо того, чтобы складывать две площади окружности, их достаточно просто умножить на «2».
С основаниями определились. Боковая поверхность цилиндра в развороте – это прямоугольник.
Площадь прямоугольника находится, как произведение смежных сторон. А так как одна из сторон описывает длину окружности основания, то можно воспользоваться формулой:
А значит, общая площадь поверхности цилиндра:
Поверхность конуса
Конус состоит из боковой поверхности, а также из основания в виде окружности. Для нахождения полной площади поверхности следует найти площадь каждой составляющей.
Читайте также: Цилиндр для проверки труб
Площадь основания: S = πR 2
Площадь боковой поверхности: S = πRl , где l – образующая.
Следовательно, общая площадь поверхности конуса находится, как сумма площадей, описанных выше:
Поверхность сферы
Для нахождения площади поверхности шара необходимо воспользоваться формулой для площади круга, умножив её на «4»:
Для нахождения площади некоторого сегмента шара можно воспользоваться следующей формулой:
S = 2πRH , где Н – высота исследуемого сегмента.
Видео:Площадь поверхности пирамиды | Геометрия 11 классСкачать

Формулы площади поверхности тел
Площадь поверхности геометрической фигуры измеряется в квадратных единицах. Очень часто используется в повседневной жизни, в строительстве, на производствах. Например, нужно вам покрасить комнату, зная сколько краски используется на кв. метр, и площади стен комнаты легко можно вычислить, сколько всего вам нужно купить краски.
Различают два вида площадей поверхности тел: Sбок — площадь боковой поверхности тела, и Р — площадь полной поверхности тела, которая равна сумме площадей боковой поверхности и основания тела.
Формула площади поверхности призмы
Площадь боковой поверхности прямой призмы равна периметру основания умноженному на высоту призмы (высота=боковому ребру).
р — периметр основания;
l — боковое ребро.
Формула площади поверхности куба
Площадь боковой поверхности куба равна числу боковых граней умноженному на квадрат ребра.
Площадь полной поверхности куба равна числу всех граней куба умноженному на квадрат ребра.
а — ребро куба.
Формула площади поверхности пирамиды
1) Правильная пирамида:
Sбок = 1/2pA
p — периметр основания;
A — апофема.
S — площадь основания;
φ — угол между боковой гранью и основанием пирамиды.
Sбок = Sгр n
Sгр — площадь одной боковой грани;
n — количество боковых граней пирамиды.
2) Правильная усеченная пирамида:
A — апофема.
Р — площадь полной поверхности правильной усеченной пирамиды;
Sбок — площадь боковой поверхности правильной усеченной пирамиды;
Формула площади поверхности цилиндра
Sбок = 2πrh = πdh
P = 2πr 2 +2πrh = 2π(r+h)
P — площадь полной поверхности цилиндра;
r — радиус цилиндра;
d — диаметр цилиндра;
h — высота цилиндра.
Формула площади поверхности конуса
1) Прямой круговой конус:
Читайте также: Течет цилиндр подъема кабины
P = πr 2 + πrl= πr(r+l)
P — площадь полной поверхности конуса;
r -радиус конуса;
d -диаметр конуса;
l — образующая конуса.
2) Усеченный прямой круговой конус:
P — площадь полной поверхности усеченного конуса;
d1, d2 — диаметры оснований усеченного конуса;
l — образующая усеченного конуса.
Формула площади поверхности шара (сферы)
Шар — тело, созданное вращением полукруга вокруг диаметра.
Сфера — поверхность шара.
Формула площади поверхности сферического сегмента
Сферический сегмент — часть сферы, что отсекается от сферы плоскостью.
Формула площади поверхности шарового сегмента
Шаровой сегмент — часть шара, что отсекается от шара плоскостью, и ограничивается кругом (основание шарового сегмента) и сферическим сегментом.
Sшар. сегм. = π(2Rh+a 2 )=π(h 2 +2a 2 )
R — радиус шара;
D — диаметр шара;
h — высота сегмента;
a — радиус основания сегмента.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Как найти площадь полной поверхности призмы пирамиды цилиндра конуса
Объем куба равен кубу длины его грани.
Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Видео:Площадь полной поверхности цилиндраСкачать

Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда
Видео:Найти площадь поверхности правильной четырехугольной пирамидыСкачать

Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда
Видео:10 класс — Задачи на площади боковой и полной поверхности пирамидыСкачать
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Видео:Площадь поверхности призмы. Практическая часть. 11 класс.Скачать
Объем правильного тетраэдра
Формула объема правильного тетраэдра
Видео:Пирамида. 11 класс.Скачать

Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Видео:60. Площадь поверхности цилиндраСкачать

Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Объем шара
Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи.
Площадь куба
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда
Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра