- Касательная прямая к сфере. Касательная плоскость к сфере
- Сфера, вписанная в цилиндр
- Отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар
- Площадь поверхности шара вписанного в цилиндр
- Найти площадь поверхности:
- Сфера, вписанная в цилиндр
- Площадь боковой поверхности цилиндра через радиус основания и высоту
- Через диаметр
- Основные утверждения
- Вместе с этой задачей также решают:
- Площадь полной поверхности цилиндра через радиус основания и высоту
- Отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар
- Касательная прямая к сфере. Касательная плоскость к сфере
- Решение
- Примеры задач
- Вписанный в шар цилиндр
- Нахождение площади поверхности вписанного в цилиндр шара
- Формула расчета площади шара
- Способы вписать шар в цилиндр
- Примеры задач
Видео:Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шараСкачать

Касательная прямая к сфере. Касательная плоскость к сфере
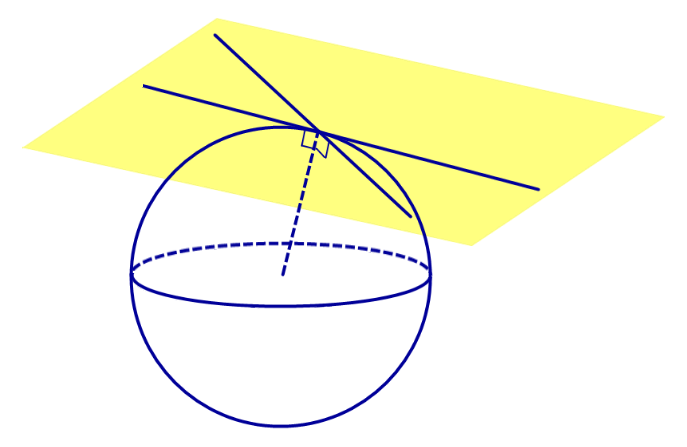
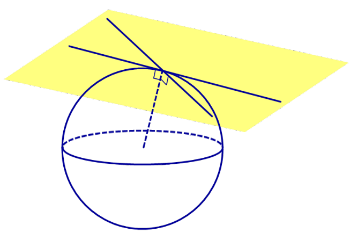
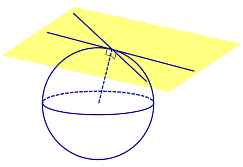
Определение 1. Прямую называют касательной к сфере (прямой, касающейся сферы), если эта прямая имеет со сферой единственную общую точку. Общую точку касательной прямой и сферы называют точкой касания (рис. 1).
Прямая касается сферы тогда и только тогда, когда эта прямая проходит через точку касания и перпендикулярна радиусу сферы, проведенному в точку касания.
Множество всех прямых, касающихся сферы в некоторой точке, образуют касательную плоскость к сфере в этой точке (рис.2).
Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем только одну.
Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем плоскость перпендикулярна радиусу сферы, проведенному в эту точку.
Общую точку сферы и ее касательной плоскости называют точкой касания .
Видео:ЕГЭ. Задача 8. Шар вписан в цилиндрСкачать

Сфера, вписанная в цилиндр
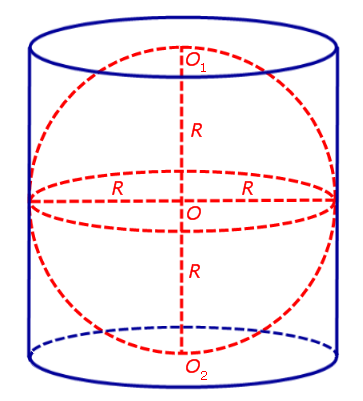
Определение 2. Сферой, вписанной в цилиндр, называют такую сферу, которая касается плоскостей обоих оснований цилиндра, а каждая образующая цилиндра является касательной к сфере (рис. 3).
Определение 3. Если сфера вписана в цилиндр, то цилиндр называют описанным около сферы .
Из рисунка 3 видно, что справедливы следующие два утверждения.
Утверждение 1. Около любой сферы можно описать цилиндр.
Утверждение 2. В цилиндр можно вписать сферу тогда и только тогда, когда высота цилиндра равна диаметру его основания.
Замечание. В том случае, когда в цилиндр можно вписать сферу, радиус вписанной сферы равняется радиусу основания цилиндра.
Видео:Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндраСкачать

Отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар
Задача. Найти отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар.
Видео:Шар вписан в цилиндр 5 задание проф. ЕГЭ по математикеСкачать

Площадь поверхности шара вписанного в цилиндр
Видео:ЕГЭ по математике. Базовый уровень. Задание 13. Около шара описан цилиндр. Площадь поверхностиСкачать

Найти площадь поверхности:
Площадь поверхности шара формула:
Sш = 4 π R 2 , где R – радиус шара, π – число пи
Читайте также: Главный тормозной цилиндр для субару легаси
Площадь поверхности цилиндра формула:
Sц = 2 π R 2 + 2 π R . 2 R = 6 π R 2 , где R – радиус цилиндра, π – число пи
Видео:60. Площадь поверхности цилиндраСкачать

Сфера, вписанная в цилиндр
Определение 2. Сферой, вписанной в цилиндр, называют такую сферу, которая касается плоскостей обоих оснований цилиндра , а каждая образующая цилиндра является касательной к сфере (рис. 3).
Определение 3. Если сфера вписана в цилиндр, то цилиндр называют описанным около сферы .
Из рисунка 3 видно, что справедливы следующие два утверждения.
Утверждение 1. Около любой сферы можно описать цилиндр.
Утверждение 2. В цилиндр можно вписать сферу тогда и только тогда, когда высота цилиндра равна диаметру его основания .
Замечание. В том случае, когда в цилиндр можно вписать сферу, радиус вписанной сферы равняется радиусу основания цилиндра.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Площадь боковой поверхности цилиндра через радиус основания и высоту
Формула для нахождения боковой поверхности цилиндра через высоту и радиус основания:
, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.
Видео:Сфера и шар. Сечение сферы. Вписанная и описанная сфераСкачать

Через диаметр
Как известно, диаметр шара равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы:
S = 4 π (d/2) 2
Видео:11 класс. Геометрия. Сфера и шар. Объем шара и площадь поверхности. 05.05.2020.Скачать

Основные утверждения
- Поверхность шара в четыре раза больше площади его большого круга.
- Поверхность шарового сегмента равна площади круга, имеющего радиусом отрезок, проведённый от вершины сегмента к окружности, служащей ему основанием.
- Цилиндр, описанный вокруг шара, имеет объём, равный трём вторым объёма шара, и площадь поверхности, равную трём вторым площади поверхности шара.
Видео:#140. Задание 8: шарСкачать

Вместе с этой задачей также решают:
Найдите объём многогранника, вершинами которого являются вершины $A,B, C,B_1$ прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB = 6, AD = 6$ и $AA_1 = 8$.
Найдите объём многогранника, вершинами которого являются вершины $A,B,C_1,B_1$ прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB = 3 , AD = 5$ и $AA_1 = 4$.
В сосуд, имеющий форму правильной треугольной призмы, налили 1800 см 3 воды и полностью погрузили в неё деталь. При этом уровень жидкости поднялся с отметки 24 см до отметки 26 см.
Объём правильной четырёхугольной пирамиды SABCD равен 16. Точка E – середина ребра SB. Найдите объём пирамиды EABC.
Видео:Видеоурок по математике "Цилиндр"Скачать

Площадь полной поверхности цилиндра через радиус основания и высоту
Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:
, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.
Видео:Задача на шар. Найти площадь поверхности - bezbotvyСкачать

Отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар
Задача. Найти отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар.
Читайте также: Определите объем камеры сгорания рабочий объем цилиндра полный объем цилиндра
Решение. Если R – радиус шара, то объем шара вычисляется по формуле
У описанного около сферы цилиндра радиус основания равен R , а высота равна 2R . Поэтому объем цилиндра равен
Видео:Площадь сферыСкачать

Касательная прямая к сфере. Касательная плоскость к сфере
Определение 1. Прямую называют касательной к сфере (прямой, касающейся сферы), если эта прямая имеет со сферой единственную общую точку. Общую точку касательной прямой и сферы называют точкой касания (рис. 1).
Прямая касается сферы тогда и только тогда, когда эта прямая проходит через точку касания и перпендикулярна радиусу сферы , проведенному в точку касания.
Множество всех прямых, касающихся сферы в некоторой точке, образуют касательную плоскость к сфере в этой точке (рис.2).
Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем только одну.
Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем плоскость перпендикулярна радиусу сферы , проведенному в эту точку.
Общую точку сферы и ее касательной плоскости называют точкой касания .
Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Решение
Из рисунка, указанного в условии, видно, что, с одной стороны, диаметр шара является диаметром окружности основания цилиндра, а с другой стороны, является высотой цилиндра. Пусть радиус шара равен R , тогда его диаметр равен 2 R , значит, высота цилиндра H равна 2 R . Находим площадь полной поверхности цилиндра: S полн. пов. цил. = 2 S осн. цил. + S бок. пов. цил. = 2pi R^2 + 2pi RH.
2pi R^2 + 2pi RH = 2pi R^2 + 2pi Rcdot 2R = 6pi R^2. По условию 24 = 6pi R^2. Отсюда pi R^2 = 4. Так как S пов. шара = 4pi R^2, то искомая площадь равна 4cdot 4 = 16.
Видео:11 класс, 23 урок, Площадь сферыСкачать

Примеры задач
Задание 1
Вычислите площадь поверхности шара, если его радиус составляет 7 см.
Решение:
Воспользуемся первой формулой (через радиус):
S = 4 ⋅ 3,14 ⋅ (7 см) 2 = 615,44 см 2 .
Задание 2
Площадь поверхности шара равна 200,96 см 2 . Найдите его диаметр.
Решение:
Выведем величину диаметра из соответствующей формулы расчета площади:
Видео:Как запомнить площадь поверхности цилиндра #математикапрофиль #геометрияегэСкачать

Вписанный в шар цилиндр
Рассмотрим комбинацию тел: шар и вписанный в шар цилиндр.
Цилиндр вписан в шар, если окружности его оснований лежат на поверхности шара. В этом случае говорят также, что шар описан вокруг цилиндра. Центр шара лежит на середине оси цилиндра.
Как и при решении задач на шар, вписанный в цилиндр , чаще всего рассматривают сечение комбинации тел плоскостью, проходящей через ось цилиндра. Это сечение представляет собой вписанный в окружность прямоугольник, стороны которого равны высоте конуса и диаметру его основания. Центр окружности лежит на пересечении диагоналей прямоугольника.
Читайте также: Давление в цилиндрах луаз
Рассмотрим пример такого осевого сечения. Здесь точка O — центр описанного около цилиндра шара, BD — диаметр шара, OD=R — радиус шара, AB=H — образующая и высота цилиндра, AD — диаметр цилиндра, FD=r — радиус цилиндра.
(как вписанный и центральный углы, опирающиеся на одну дугу AD).
Треугольник AOD — равнобедренный (AO=OD=R), в нем OF=H/2 — высота, медиана и биссектриса.
Треугольник OFD — прямоугольный. По теореме Пифагора получаем соотношение, связывающее радиус шара с радиусом и высотой вписанного в шар цилиндра:
Это же соотношение можно получить из прямоугольного треугольника ABD: по теореме Пифагора
Видео:Стереометрия, номер 46.1Скачать

Нахождение площади поверхности вписанного в цилиндр шара
В данной публикации мы разберем варианты того, как можно вписать шар в цилиндр, а также, как исходя из этого определить его радиус (диаметр) и посчитать площадь поверхности.
Видео:11 класс, 25 урок, Сфера, вписанная в цилиндрическую поверхностьСкачать

Формула расчета площади шара
Для начала давайте вспомним общую формулу, по которой рассчитывается площадь поверхности шара:
S = 4 π R 2
или S = 4 π (d/2) 2 , где d = 2R.
Видео:#131. Задание 8: комбинация телСкачать

Способы вписать шар в цилиндр
Теперь давайте разберемся, каким образом можно вписать шар в цилиндр. В данном случае возможно несколько вариантов:
1. Шар касается оснований и боковой поверхности цилиндра
- радиус (диаметр) цилиндра является, в том числе, и радиусом (диаметром) шара;
- высота цилиндра – это диаметр шара.
2. Шар касается только оснований цилиндра
Радиус шара равен половине высоты цилиндра, а диаметр – полной высоте.
3. Шар касается только боковой поверхности цилиндра
Радиус (диаметр) цилиндра – это и есть радиус (диаметр) шара.
Примечание: Выяснив радиус или диаметр шара далее остается только воспользоваться формулой для расчета площади его поверхности.
Примеры задач
Задание 1
Шар вписан в цилиндр радиусом 15 см таким образом, что соприкасается и с основанием, и с боковой поверхностью последнего. Найдите площадь поверхности шара.
Решение:
Исходя из условий задачи, мы имеем дело с первым из трех описанных вариантов выше. А это значит, что радиус шара, также, равняется 15 см. Следовательно, площадь составляет:
S = 4 ⋅ 3,14 ⋅ (15 см) 2 = 2826 см 2 .
Задание 2
Площадь поверхности шара равняется 1519,76 см 2 , и он вписан в цилиндр таким образом, что касается его оснований. Найдите высоту цилиндра.
Решение:
Для начала найдем радиус шара, которые равен:
Высота цилиндра равна двум радиусам шара или его диаметру (2-ой вариант, рассмотренный в разделе выше):
h = 2R = 2 ⋅ 11 см = 22 см.