Как найти площадь сечения цилиндра который не пересекает оси

Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются диаметр основания и высота.

Сечение цилиндра — это изображение фигуры, образованной рассечением цилиндра плоскостью в поперечном или продольном направлении.

Формула для расчета площади основания цилиндра:

Формула для расчета площади осевого сечения цилиндра:

d — диаметр цилиндра;
h — высота цилиндра.

Формула для расчета площади параллельного оси сечения цилиндра (бокового сечения цилиндра):

a — хорда основания цилиндра;
h — высота цилиндра.

Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного или продольного сечения цилиндра, если известны диаметр цилиндра, длина хорды и высота цилиндра. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения цилиндра (площадь осевого сечения цилиндра, площадь параллельного сечения цилиндра, площадь бокового сечения цилиндра и площади основания цилиндра).

Видео:Радиус основания цилиндра равен 26. Найти площадь сеченияСкачать

Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников

Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов

12(B13). Найти площадь сечения цилиндра, параллельного его оси (вар. 52)

Радиус основания цилиндра равен 5, высота 4. Найдите площадь сечения этого цилиндра плоскостью, параллельной его оси и отстоящей от нее на расстояние 3.

Сечение цилиндра — это прямоугольник ABED, одна его сторона ВЕ равна 4, т.к. является высотой цилиндра. Вторую сторону АВ найдём из треугольника АСВ. Это равнобедренный треугольник, его боковая сторона равна радиусу цилиндра, а высота, опущенная на основание — это данное расстояние от сечения до оси. Из треугольника АСН с гипотенузой 5 и катетом 3 найдём второй катет — 4. Катет АН — это половина основания АВ, т.к. СН — медиана, т.е. АВ = 8. Найдём площадь сечения, перемножив стороны прямоугольника. S = 8 · 4. Ответ: 32

Автор: Ольга Себедаш Просмотров: 60917

Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов

Читайте также: Нет искры во втором цилиндре ваз 2112

Комментарии к этой задаче:

Комментарий добавил(а): диляна
Дата: 2017-03-26

Комментарий добавил(а): надя
Дата: 2014-01-26

причем тут треугольник вообще. взяли так просто и подрисовали кверху. зачем он нужен прямоугольнику? почему нельзя умножить 5 на 4. еще жизнь себе усложнять

Комментарий добавил(а): Ольга Себедаш
Дата: 2014-01-26

Наденька, умножай пять на четыре, кто мешает.

Комментарий добавил(а): Петр
Дата: 2014-03-21

Браво! Очень доходчиво и вообще 5+!!

Комментарий добавил(а): Оля
Дата: 2014-03-29

простите, а где решение 51 варианта?

Комментарий добавил(а): Александр
Дата: 2014-04-13

У меня нет слов все так просто , автору уважение.

Комментарий добавил(а): михаил
Дата: 2014-07-21

все хорошо объяснили спасибо большое теперь я понял что это легко и теперь буду к вам обращатся чтоб удачно здать экзамены а потом поступить в вуз естественно здавать я буду без вашей помощи а сам просто здесь я практикуюсь и совершенству ю свои умения

Комментарий добавил(а): Анна
Дата: 2016-04-08

Комментарий добавил(а): ส็็็็็็็็&
Дата: 2020-12-03

Комментарий добавил(а):
Дата: 2020-12-03

Видео:№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать

Как определить площадь сечения цилиндра, конуса, призмы и пирамиды? Формулы

На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Объемные фигуры

Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.

Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).

Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Цилиндр

Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:

Читайте также: Цилиндры для офисных кресел

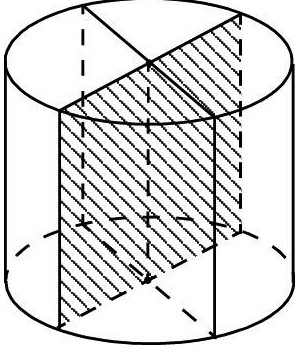
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.

Площадь круглого сечения рассчитывается по формуле:

Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:

Видео:60. Площадь поверхности цилиндраСкачать

Сечения конуса

Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:

• круглое;
• эллиптическое;
• параболическое;
• гиперболическое;
• треугольное.

Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.

Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:

Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z Понравилась статья? Поделись с друзьями:

Видео:Видеоурок по математике "Цилиндр"Скачать

Сечение цилиндра: определение, виды, его образующая

Видео:Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать

Кратко о цилиндре

Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.

Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.

Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Осевое сечение

Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Как найти площадь сечения

где \(d\) — диаметр, а \(h\) — высота всей фигуры.

Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).

Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

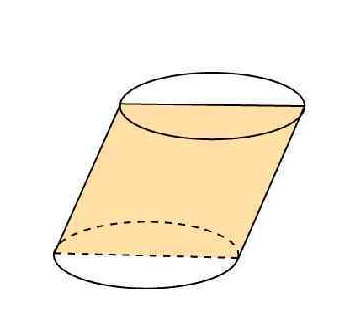
Осевое сечение наклонного цилиндра

Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.

Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:

Видео:Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

Примеры задач

Рассмотрим пару задач на осевое сечение с решениями.

Задача 1

Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?

Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:

Читайте также: Не открываются заслонки впускных каналов 1 ряда цилиндров

Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:

\(Sц = 2pi * r * (r + 2r) = 6 * pi * r²\)

Исходя из этого, будем выражать радиус:

Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:

Подставим известные данные ( \(Sц = 100см^2\) ) и получим площадь сечения \(S = 21,23 см²\) .

Ответ: \(S = 21,23 см²\) .

Задача 2

Дано: ABCD — осевое сечение цилиндра. Площадь сечения \(Sc\) равна \(10 м²\) , а площадь основания \(Sо— 5 м²\) . Найти высоту цилиндра.

Так как площадь основания — круг, то \(Sо = pi * r²\) . Тогда \(r = √(Sо/pi) = √(5/pi).\)

Так как площадь сечения — прямоугольник, то \(Sc = AB * BC = h * 2r.\) Тогда \(h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).\)

Видео:✓ Площадь сечения | ЕГЭ-2018. Задание 14. Математика. Профильный уровень | Борис ТрушинСкачать

Как найти площадь сечения цилиндра который не пересекает оси

Высота цилиндра равна 5, а радиус основания 10.

а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.

б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.

а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.

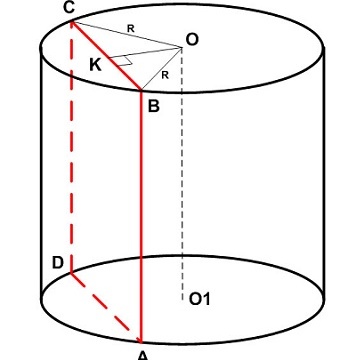
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO₁, — прямоугольник ABB₁A₁ (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA₁ = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда

В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).

Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.

В школьном курсе задачи о наклонных цилиндрах не рассматриваются.

📹 Видео

Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Нахождение площади боковой поверхности цилиндраСкачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

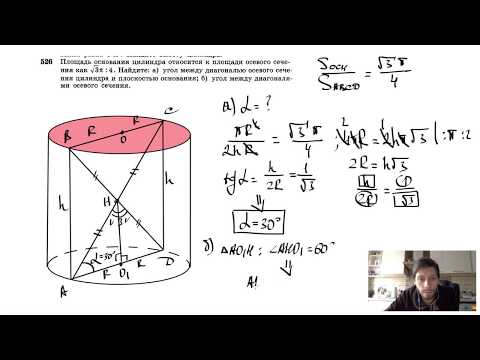
№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать

Построить сечение цилиндра с плоскостью общего положения.Скачать