Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются диаметр основания и высота.
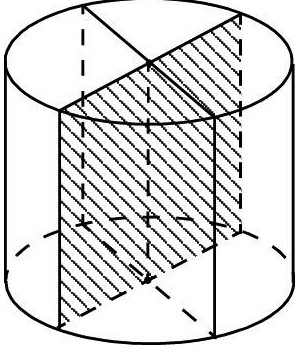
Сечение цилиндра — это изображение фигуры, образованной рассечением цилиндра плоскостью в поперечном или продольном направлении.
Формула для расчета площади основания цилиндра:
Формула для расчета площади осевого сечения цилиндра:
d — диаметр цилиндра;
h — высота цилиндра.
Формула для расчета площади параллельного оси сечения цилиндра (бокового сечения цилиндра):
a — хорда основания цилиндра;
h — высота цилиндра.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного или продольного сечения цилиндра, если известны диаметр цилиндра, длина хорды и высота цилиндра. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения цилиндра (площадь осевого сечения цилиндра, площадь параллельного сечения цилиндра, площадь бокового сечения цилиндра и площади основания цилиндра).
- Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
- Геометрическая фигура
- Прямой и наклонный цилиндры
- Осевое сечение прямого цилиндра
- Осевое сечение наклонного цилиндра
- Задача с прямым цилиндром
- Цилиндры
- Основные определения и свойства цилиндра
- Сечения цилиндра
- Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра
- Сечение цилиндра: определение, виды, его образующая
- Кратко о цилиндре
- Осевое сечение
- Как найти площадь сечения
- Осевое сечение наклонного цилиндра
- Примеры задач
- Задача 1
- Задача 2
- Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
- Площадь поперечного сечения
- Область применения
- Как рассчитать параметры труб
- Для чего нужны расчеты параметров труб
- Внутренний и наружный диаметр, толщина стенки, радиус
- Расчет площади поверхности трубы
- Расчет веса
- Как высчитать площадь поперечного сечения
- Геометрическая фигура
- Как связан цилиндр с вписанной в него или описанной около него призмой?
- Виды цилиндров
- Нюансы расчета площади по внутренней стороне трубы
- Калькулятор расчета площади трубы под окраску
- Отличия скошенного цилиндра
- Длина окружности
- Прямой и наклонный цилиндры
Видео:Цилиндр - расчёт площади, объёма.Скачать

Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
Цилиндр — это симметричная пространственная фигура, свойства которой рассматривают в старших классах школы в курсе стереометрии. Для его описания используют такие линейные характеристики, как высота и радиус основания. В данной статье рассмотрим вопросы касательно того, что такое осевое сечение цилиндра, и как рассчитать его параметры через основные линейные характеристики фигуры.
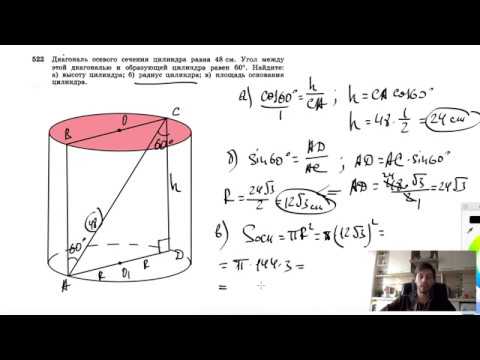
Видео:№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
Геометрическая фигура
Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.
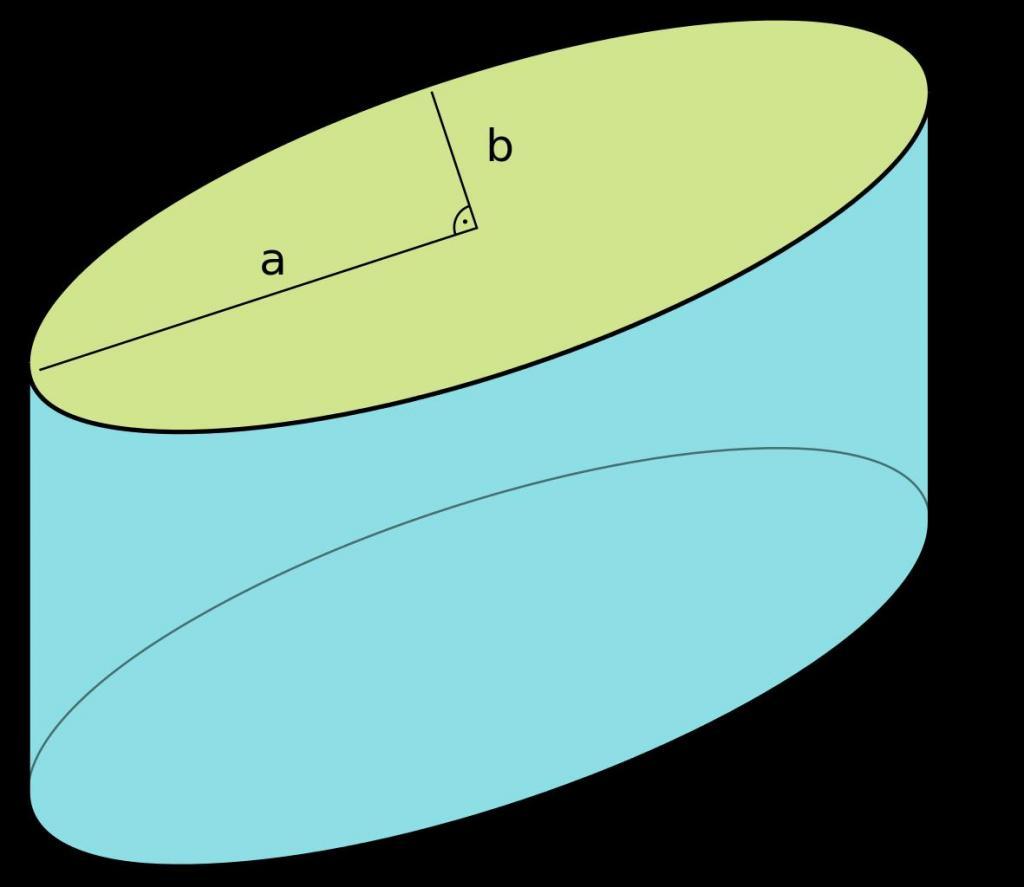
На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.
Здесь отрезок длиной h является его образующей и высотой.
Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Прямой и наклонный цилиндры
Перед тем как переходить к рассмотрению осевого сечения цилиндров, расскажем, какие типы этих фигур бывают.
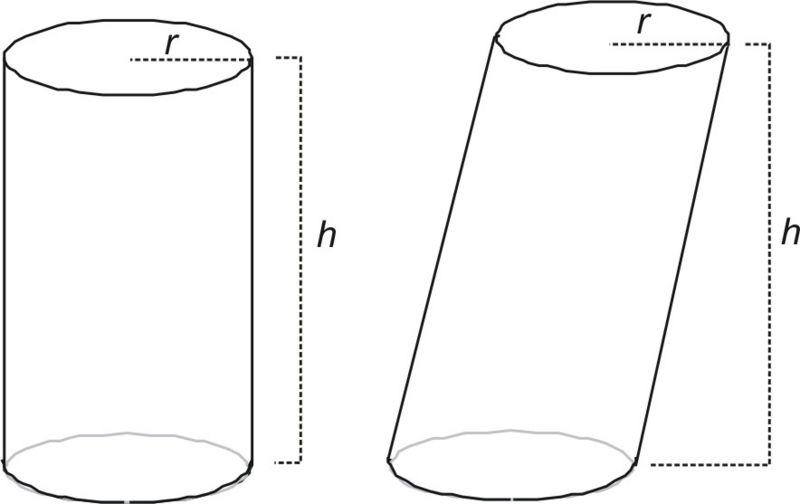
Если образующая линия перпендикулярна основаниям фигуры, тогда говорят о прямом цилиндре. В противном случае цилиндр будет наклонным. Если соединить центральные точки двух оснований, то полученная прямая называется осью фигуры. Приведенный рисунок демонстрирует разницу между прямым и наклонным цилиндрами.
Видно, что для прямой фигуры длина образующего отрезка совпадает со значением высоты h. Для наклонного цилиндра высота, то есть расстояние между основаниями, всегда меньше длины образующей линии.
Далее охарактеризуем осевые сечения обоих типов цилиндров. При этом будем рассматривать фигуры, основаниями которых является круг.
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Осевое сечение прямого цилиндра
Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.
В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.
Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.
Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:
Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.
Видео:№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Осевое сечение наклонного цилиндра
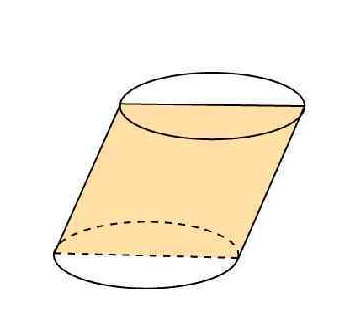
Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны — это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же — длина образующего отрезка. Обозначим ее b.
Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:
Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:
Здесь l1 и l2 — длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.
Видео:60. Площадь поверхности цилиндраСкачать

Задача с прямым цилиндром
Покажем, как использовать полученные знания для решения следующей задачи. Пусть дан круглый прямой цилиндр. Известно, что осевое сечение цилиндра — квадрат. Чему равна площадь этого сечения, если площадь поверхности всей фигуры составляет 100 см2?
Для вычисления искомой площади необходимо найти либо радиус, либо диаметр основания цилиндра. Для этого воспользуемся формулой для общей площади Sf фигуры:
Поскольку сечение осевое представляет собой квадрат, то это означает, что радиус r основания в два раза меньше высоты h. Учитывая это, можно переписать равенство выше в виде:
Теперь можно выразить радиус r, имеем:
Поскольку сторона квадратного сечения равна диаметру основания фигуры, то для вычисления его площади S будет справедлива следующая формула:
Мы видим, что искомая площадь однозначно определяется площадью поверхности цилиндра. Подставляя данные в равенство, приходим к ответу: S = 21,23 см2.
Видео:Радиус основания цилиндра равен 26. Найти площадь сеченияСкачать

Цилиндры
Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Основные определения и свойства цилиндра
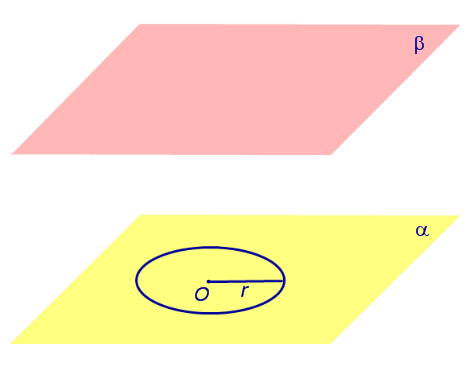
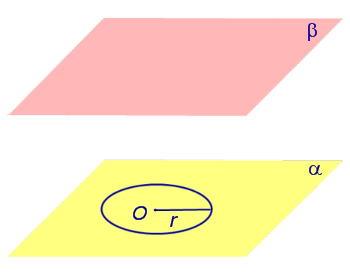
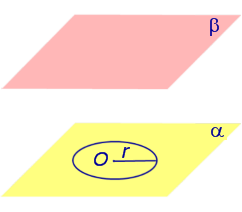
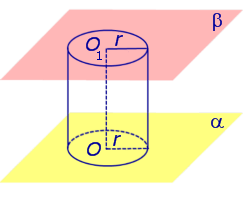
Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O1 которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).
Читайте также: Какое должно быть давление в цилиндрах ваз 2114
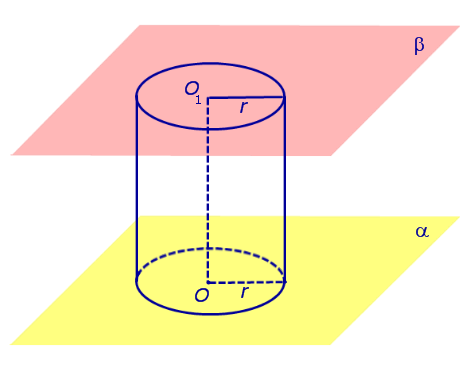
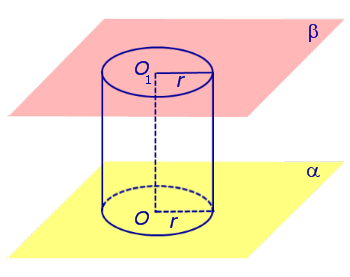
Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .
Совокупность всех образующих цилиндра называют цилиндрической поверхностью .
Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .
Отрезок OO1 называют осью цилиндра .
Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .
Круги с центрами O и O1 на плоскостях α и β , называют основаниями цилиндра .
Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .
Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.
Замечание 3. Прямая OO1 является осью симметрии цилиндра, а середина отрезка OO1 является центром симметрии цилиндра.
Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Сечения цилиндра
Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
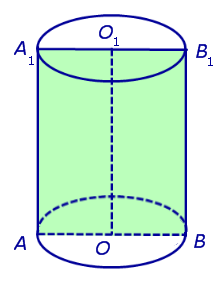
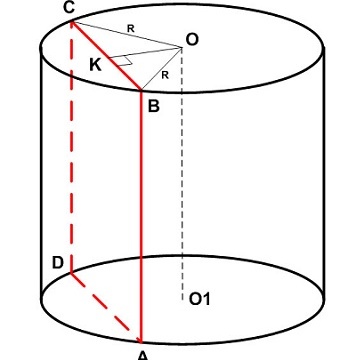
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).
На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA1B1B .
Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .
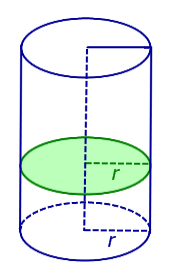
Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).
Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .
Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».
Видео:№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра
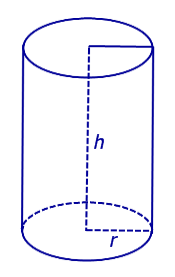
Для цилиндра с радиусом r и высотой h (рис. 5)
введем следующие обозначения
| V | объем цилиндра |
| Sбок | площадь боковой поверхности цилиндра |
| Sполн | площадь полной поверхности цилиндра |
| Sосн | площадь основания цилиндра |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:
при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
Видео:Видеоурок по математике "Цилиндр"Скачать

Сечение цилиндра: определение, виды, его образующая
Видео:№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать
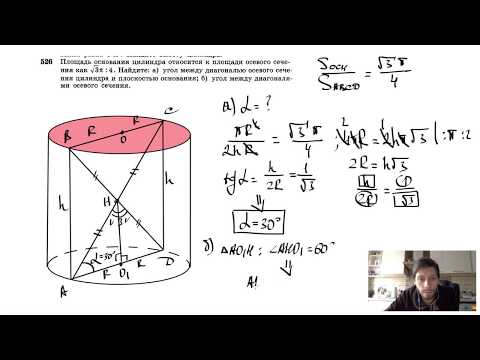
Кратко о цилиндре
Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.
Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Осевое сечение
Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Видео:Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

Как найти площадь сечения
где \(d\) — диаметр, а \(h\) — высота всей фигуры.
Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).
Видео:№542. Угол между образующей цилиндра и диагональю осевого сечения равен φ, площадь основанияСкачать
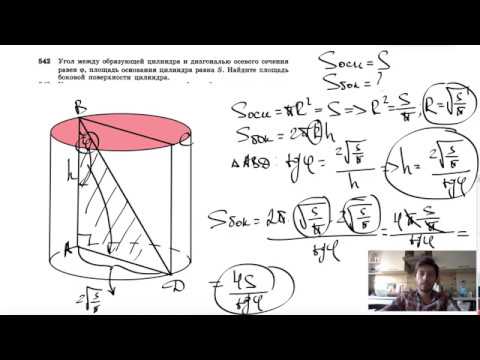
Осевое сечение наклонного цилиндра
Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.
Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:
Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Примеры задач
Рассмотрим пару задач на осевое сечение с решениями.
Задача 1
Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?
Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:
Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:
\(Sц = 2pi * r * (r + 2r) = 6 * pi * r²\)
Исходя из этого, будем выражать радиус:
Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:
Подставим известные данные ( \(Sц = 100см^2\) ) и получим площадь сечения \(S = 21,23 см²\) .
Ответ: \(S = 21,23 см²\) .
Задача 2
Дано: ABCD — осевое сечение цилиндра. Площадь сечения \(Sc\) равна \(10 м²\) , а площадь основания \(Sо— 5 м²\) . Найти высоту цилиндра.
Так как площадь основания — круг, то \(Sо = pi * r²\) . Тогда \(r = √(Sо/pi) = √(5/pi).\)
Так как площадь сечения — прямоугольник, то \(Sc = AB * BC = h * 2r.\) Тогда \(h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).\)
Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
Сегодня нам предстоит небольшой экскурс в школьные программы геометрии и физики. Мы вспомним, как вычисляется площадь поперечного сечения трубы и ее внутренний объем. Кроме того, нам предстоит выяснить, как изменения диаметра трубопровода действуют на давление в потоке жидкости. Итак, в путь.
На фото – водогазопроводные трубы. Нам предстоит научиться вычислять их внутреннее сечение.
Видео:Нахождение площади боковой поверхности цилиндраСкачать

Площадь поперечного сечения
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения.
Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле.
Площадь сечения круга или шара можно найти по формуле:
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма.
Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
Из нее можно вывести такую формулу:
c = S*q*r*t*(a2 + b2)
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Читайте также: Габаритные размеры цилиндра это
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
где 2а – значение хорды, расчета площади поперечного сечения.
Вернуться к просмотру справок по дисциплине “Геометрия”
Видео:Как отрезать трубу под 45 градусов с минимальным зазоромСкачать

Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

Как рассчитать параметры труб
При строительстве и обустройстве дома трубы не всегда используются для транспортировки жидкостей или газов.
Часто они выступают как строительный материал — для создания каркаса различных построек, опор для навесов и т.д. При определении параметров систем и сооружений необходимо высчитать разные характеристики ее составляющих.
В данном случае сам процесс называют расчет трубы, а включает он в себя как измерения, так и вычисления.
Для чего нужны расчеты параметров труб
В современном строительстве используются не только стальные или оцинкованные трубы. Выбор уже довольно широк — ПВХ, полиэтилен (ПНД и ПВД), полипропилен, металлопластк, гофрированная нержавейка.
Они хороши тем, что имеют не такую большую массу, как стальные аналоги. Тем не менее, при транспортировке полимерных изделий в больших объемах знать их массу желательно — чтобы понять, какая машина нужна.
Вес металлических труб еще важнее — доставку считают по тоннажу. Так что этот параметр желательно контролировать.
То, что нельзя измерить, можно рассчитать
Знать площадь наружной поверхности трубы надо для закупки краски и теплоизоляционных материалов. Красят только стальные изделия, ведь они подвержены коррозии в отличие от полимерных. Вот и приходится защищать поверхность от воздействия агрессивных сред.
Используют их чаще для строительства заборов, каркасов для хозпостроек (гаражей, сараев, беседок, бытовок), так что условия эксплуатации — тяжелы, защита необходима, потому все каркасы требуют окраски.
Вот тут и потребуется площадь окрашиваемой поверхности — наружная площадь трубы.
При сооружении системы водоснабжения частного дома или дачи, трубы прокладывают от источника воды (колодца или скважины) до дома — под землей.
И все равно, чтобы они не замерзли, требуется утепление. Рассчитать количество утеплителя можно зная площадь наружной поверхности трубопровода.
Только в этом случае надо брать материал с солидным запасом — стыки должны перекрываться с солидным запасом.
Сечение трубы необходимо для определения пропускной способности — сможет ли данное изделие провести требуемое количество жидкости или газа. Этот же параметр часто нужен при выборе диаметра труб для отопления и водопровода, расчета производительности насоса и т.д.
Внутренний и наружный диаметр, толщина стенки, радиус
Трубы — специфический продукт. Они имеют внутренний и наружный диаметр, так как стенка у них толстая, ее толщина зависит от типа трубы и материала из которого она изготовлена. В технических характеристиках чаще указывают наружный диаметр и толщину стенки.
Внутренний и наружный диаметр трубы, толщина стенки
Имея эти два значения, легко высчитать внутренний диаметр — от наружного отнять удвоенную толщину стенки: d = D — 2*S. Если у вас наружный диаметр 32 мм, толщина стенки 3 мм, то внутренний диаметр будет: 32 мм — 2 * 3 мм = 26 мм.
Если же наоборот, имеется внутренний диаметр и толщина стенки, а нужен наружный — к имеющемуся значению добавляем удвоенную толщину стеки.
С радиусами (обозначаются буквой R) еще проще — это половина от диаметра: R = 1/2 D. Например, найдем радиус трубы диаметром 32 мм. Просто 32 делим на два, получаем 16 мм.
Измерения штангенциркулем более точные
Что делать, если технических данных трубы нет? Измерять. Если особая точность не нужна, подойдет и обычная линейка, для более точных измерений лучше использовать штангенциркуль.
Расчет площади поверхности трубы
Труба представляет собой очень длинный цилиндр, и площадь поверхность трубы рассчитывается как площадь цилиндра. Для вычислений потребуется радиус (внутренний или наружный — зависит от того, какую поверхность вам надо рассчитать) и длина отрезка, который вам необходим.
Формула расчета боковой поверхности трубы
Чтобы найти боковую площадь цилиндра, перемножаем радиус и длину, полученное значение умножаем на два, а потом — на число «Пи», получаем искомую величину. При желании можно рассчитать поверхность одного метра, ее потом можно умножать на нужную длину.
Для примера рассчитаем наружную поверхность куска трубы длиной 5 метров, с диаметром 12 см. Для начала высчитаем диаметр: делим диаметр на 2, получаем 6 см.
Теперь все величины надо привести к одним единицам измерения. Так как площадь считается в квадратных метрах, то сантиметры переводим в метры. 6 см = 0,06 м.
Дальше подставляем все в формулу: S = 2 * 3,14 * 0,06 * 5 = 1,884 м2. Если округлить, получится 1,9 м2.
Расчет веса
С расчетом веса трубы все просто: надо знать, сколько весит погонный метр, затем эту величину умножить на длину в метрах.
Вес круглых стальных труб есть в справочниках, так как этот вид металлопроката стандартизован. Масса одного погонного метра зависит от диаметра и толщины стенки.
Один момент: стандартный вес дан для стали плотностью 7,85 г/см2 — это тот вид, который рекомендован ГОСТом.
Таблица веса круглых стальных труб
В таблице Д — наружный диаметр, условный проход — внутренний диаметр, И еще один важный момент: указана масса обычных стального проката, оцинкованные на 3% тяжелее.
Таблица веса профилированной трубы квадратного сечения
Как высчитать площадь поперечного сечения
Формула нахождения площади сечения круглой трубы
Если труба круглая, площадь сечения считать надо по формуле площади круга: S = π*R2. Где R — радиус (внутренний), π — 3,14. Итого, надо возвести радиус в квадрат и умножить его на 3,14.
Читайте также: Растачивать блок цилиндров или нет
Например, площадь сечения трубы диаметром 90 мм. Находим радиус — 90 мм / 2 = 45 мм. В сантиметрах это 4,5 см. Возводим в квадрат: 4,5 * 4,5 = 2,025 см2, подставляем в формулу S = 2 * 20,25 см2 = 40,5 см2.
Геометрическая фигура
Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.
На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.
Здесь отрезок длиной h является его образующей и высотой.
Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.
Как связан цилиндр с вписанной в него или описанной около него призмой?
Иногда встречаются задачи, в которых нужно вычислить площадь цилиндра, а известны при этом некоторые элементы связанной с ним призмы. Как соотносятся эти фигуры?
Если призма вписана в цилиндр, то ее основания – равные многоугольники. Причем они вписаны в соответствующие основания цилиндра. Боковые ребра призмы совпадают с образующими.
У описанной призмы в основаниях находятся правильные многоугольники. Они описаны около кругов цилиндра, являющихся его основаниями. Плоскости, которые содержат грани призмы, касаются цилиндра по образующим.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Нюансы расчета площади по внутренней стороне трубы
Что касается внутренней поверхности трубы, то чаще всего ее площадь вычисляют для дальнейшего расчета гидродинамики транспортировки теплоносителя по всему отопительному, водоснабжающему или водоотводящему трубопроводу.
Суть такого расчета заключается в том, чтобы определить сопротивление, которое будет оказываться теплоносителю при движении по трубе. Сопротивление возникает в любом случае, т.к. между теплоносителем и внутренней стенкой трубы возникает трение.
Существуют следующие нюансы:
- Чем больше диаметр трубопровода, тем меньше гидравлическое сопротивление внутри него. Соответственно при большом диаметре можно вовсе не учитывать данный параметр.
- Также гидравлическое сопротивление очень зависимо от качества материала, из которого изготовлен трубопровод, поскольку различные шероховатости могут повлиять на скорость транспортировки теплоносителя. Данный нюанс более значим для определения гидродинамики, чем площадь внутренней поверхности трубы. Естественно, пластиковые трубы в этом плане будут куда более выгодными, чем металлические, в которых образуется ржавчина.
- Если устанавливать систему из оцинкованных металлических труб, то нужно знать не только, как посчитать квадратные метры трубы, но и то, что на таком материале постоянно образуется ржавчина и скапливаются прочие отложения.
В статье подробно описаны формулы для вычисления всевозможных линейных параметров трубопровода. Все формулы очень просты: достаточно в них подставить лишь конкретные значения. Полученные значения площадей помогут не только сэкономить на различных материалах (утеплитель, краска), но и высчитать различные особенности всей системы отопления, водоснабжения или водоотведения.
Лучше всего, используя данную статью, определить основные параметры трубопровода, прежде чем обращаться к специалистам для проведения работ различного характера.
Когда встает вопрос окраски труб, визуально кажется, что это и времени много не займет, и краски понадобится один стакан. На практике оказывается, что дело обстоит совсем иначе. Поверхность труб имеет площадь и поддается подсчету, по результатам которого вычисляется объем работ и количество материала. Площадь трубы под окраску калькулятор высчитывает за доли секунды, тогда как ручной подсчет кажется сложнейшим делом.
Газовая труба подлежит регулярной окраске
Расчет площади труб нужен тогда, когда требуется узнать расход материала и трудозатраты. Определить визуально площадь стен и прикинуть примерный расход может любой мастер, а вот сделать то же самое, когда дело касается труб или металлических конструкций намного сложнее.
Площадь труб нужно узнать, если планируются следующие работы:
- нанесение антикоррозионного покрытия;
- декоративное окрашивание;
- нанесение теплоизоляционного слоя на трубы большого диаметра.
В каждом из этих случаев требуется узнать расход материалов. Если окрашивается, например, металлическая конструкция из круглой или профильной трубы, и работы выполняются наемными рабочими, то во избежание всяческих злоупотреблений стоит заранее просчитать расход материала и трудозатраты в человеко-часах. Такой подход выгоден заказчику и вызывает уважение в глазах исполнителя.
Калькулятор расчета площади трубы под окраску
В быту расчетам на строительство отводится обычно далеко не первое место. Это касается и процесса покраски труб. Мало кто заранее просчитывает, сколько краски придется купить для этой работы. И это неправильно, потому что предварительные расчеты помогут сэкономить немалые средства. В связи с этим возникает вопрос: как рассчитать количество лакокрасочных материалов, необходимых для покраски различных труб?
Отличия скошенного цилиндра
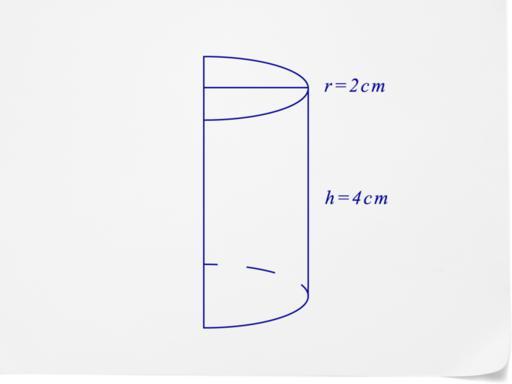
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а
под неким углом, отличным от 90° к образующим, пересекает фигуру.
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
Поскольку площадь n – угольника B1B2…Bn равна
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R:
Следствие. Длина окружности радиуса 1 равна 2π.
Прямой и наклонный цилиндры
Перед тем как переходить к рассмотрению осевого сечения цилиндров, расскажем, какие типы этих фигур бывают.
Если образующая линия перпендикулярна основаниям фигуры, тогда говорят о прямом цилиндре. В противном случае цилиндр будет наклонным. Если соединить центральные точки двух оснований, то полученная прямая называется осью фигуры. Приведенный рисунок демонстрирует разницу между прямым и наклонным цилиндрами.
Видно, что для прямой фигуры длина образующего отрезка совпадает со значением высоты h. Для наклонного цилиндра высота, то есть расстояние между основаниями, всегда меньше длины образующей линии.
Далее охарактеризуем осевые сечения обоих типов цилиндров. При этом будем рассматривать фигуры, основаниями которых является круг.