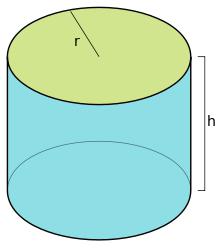
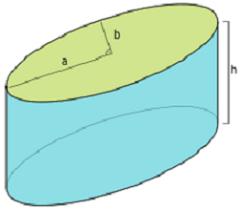
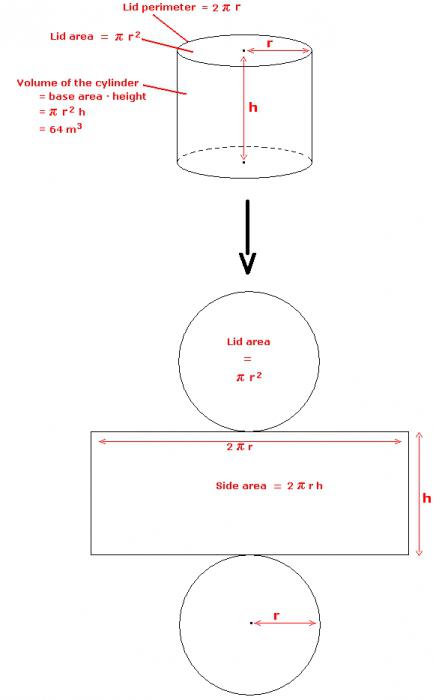
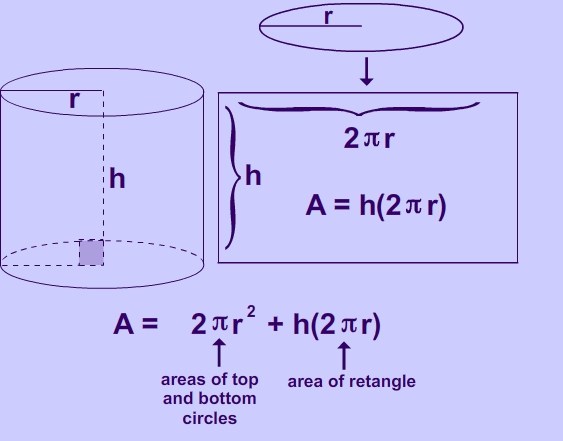
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются диаметр основания и высота.
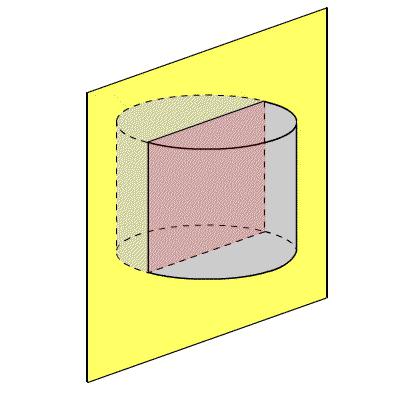
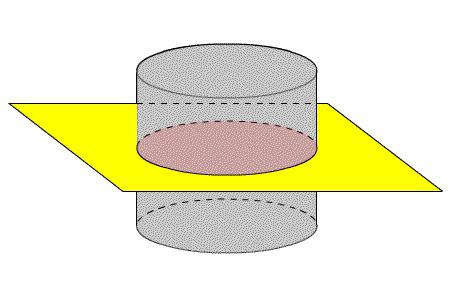
Сечение цилиндра — это изображение фигуры, образованной рассечением цилиндра плоскостью в поперечном или продольном направлении.
Формула для расчета площади основания цилиндра:
Формула для расчета площади осевого сечения цилиндра:
d — диаметр цилиндра;
h — высота цилиндра.
Формула для расчета площади параллельного оси сечения цилиндра (бокового сечения цилиндра):
a — хорда основания цилиндра;
h — высота цилиндра.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного или продольного сечения цилиндра, если известны диаметр цилиндра, длина хорды и высота цилиндра. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения цилиндра (площадь осевого сечения цилиндра, площадь параллельного сечения цилиндра, площадь бокового сечения цилиндра и площади основания цилиндра).
- Нахождение площади поверхности цилиндра: формула и задачи
- Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
- Примеры того, как вычислить площадь цилиндра
- Какое тело является цилиндром?
- Основные элементы цилиндра
- Как связан цилиндр с вписанной в него или описанной около него призмой?
- О площади боковой поверхности и основания для прямого кругового цилиндра
- О площади всей поверхности прямого кругового цилиндра
- О площадях наклонного кругового цилиндра
- Чему равны некоторые сечения прямого кругового цилиндра?
- Примеры задач
- 🎬 Видео
Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Нахождение площади поверхности цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)
Видео:№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Примеры того, как вычислить площадь цилиндра
Существует большое количество задач, связанных с цилиндром. В них нужно находить радиус и высоту тела или вид его сечения. Плюс ко всему, иногда требуется вычислить площадь цилиндра и его объем.
Видео:Видеоурок по математике "Цилиндр"Скачать

Какое тело является цилиндром?
В курсе школьной программы изучается круговой, то есть являющийся таковым в основании, цилиндр. Но выделяют еще и эллиптический вид данной фигуры. Из названия ясно, что его основанием будет эллипс или овал.
Читайте также: Хонингование блока цилиндров что это такое
Оснований у цилиндра два. Они равны друг другу и соединены отрезками, которые совмещают соответствующие точки оснований. Они называются образующими цилиндра. Все образующие параллельны друг другу и равны. Именно они составляют боковую поверхность тела.
В общем случае цилиндр — это наклонное тело. Если образующие составляют прямой угол с основаниями, то говорят уже о прямой фигуре.
Интересно, что круговой цилиндр является телом вращения. Он получается от поворота прямоугольника вокруг одной из его сторон.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Основные элементы цилиндра
Основные элементы цилиндра выглядят следующим образом.
- Высота. Она является кратчайшим расстоянием между основаниями цилиндра. Если он прямой, то высота совпадает с образующей.
- Радиус. Совпадает с тем, который можно провести в основании.
- Ось. Это прямая линия, которая содержит центры обоих оснований. Ось всегда параллельна всем образующим. В прямом цилиндре она перпендикулярна основаниям.
- Осевое сечение. Оно образуется при пересечении цилиндра плоскостью, содержащей ось.
- Касательная плоскость. Она проходит через одну из образующих и перпендикулярна осевому сечению, которое проведено через эту образующую.
Видео:№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать
Как связан цилиндр с вписанной в него или описанной около него призмой?
Иногда встречаются задачи, в которых нужно вычислить площадь цилиндра, а известны при этом некоторые элементы связанной с ним призмы. Как соотносятся эти фигуры?
Если призма вписана в цилиндр, то ее основания – равные многоугольники. Причем они вписаны в соответствующие основания цилиндра. Боковые ребра призмы совпадают с образующими.
У описанной призмы в основаниях находятся правильные многоугольники. Они описаны около кругов цилиндра, являющихся его основаниями. Плоскости, которые содержат грани призмы, касаются цилиндра по образующим.
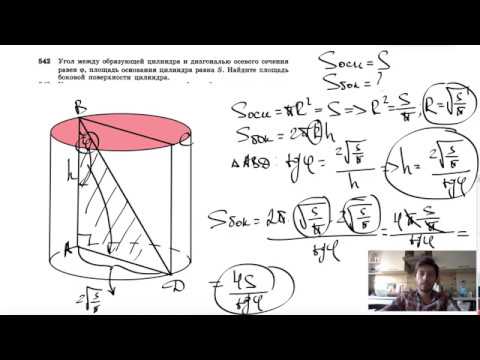
Видео:№542. Угол между образующей цилиндра и диагональю осевого сечения равен φ, площадь основанияСкачать
О площади боковой поверхности и основания для прямого кругового цилиндра
Если сделать развертку боковой поверхности, то получится прямоугольник. Его стороны будут совпадать с образующей и длиной окружности основания. Поэтому боковая площадь цилиндра будет равна произведению этих двух величин. Если записать формулу, то получится следующее:
где н — образующая, l — длина окружности.
Причем последний параметр вычисляется по формуле:
l = 2 π * r,
здесь r — радиус окружности, π — число «пи», равное 3,14.
Поскольку основание — круг, то его площадь вычисляется с помощью такого выражения:
Sосн = π * r 2 .
Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

О площади всей поверхности прямого кругового цилиндра
Так как она образована двумя основаниями и боковой поверхностью, то нужно сложить эти три величины. То есть полная площадь цилиндра будет вычисляться по формуле:
Sпол = 2 π * r * н + 2 π * r 2 .
Часто ее записывают в другом виде:
Sпол= 2 π * r (н + r).
Видео:Осевое сечение цилиндра. Площадь полной поверхности цилиндраСкачать

О площадях наклонного кругового цилиндра
Что касается оснований, то там все формулы те же, ведь они по-прежнему круги. А вот боковая поверхность уже не дает прямоугольника.
Для расчета площади боковой поверхности наклонного цилиндра потребуется перемножить значения образующей и периметра сечения, которое будет перпендикулярно выбранной образующей.
где х — длина образующей цилиндра, Р — периметр сечения.
Сечение, кстати, лучше выбирать такое, чтобы оно образовывало эллипс. Тогда будут упрощены расчеты его периметра. Длина эллипса вычисляется по формуле, которая дает приблизительный ответ. Но его часто бывает достаточно для задач школьного курса:
где «а» и «в» — полуоси эллипса, то есть расстояния от центра до ближайшей и самой дальней его точек.
Площадь всей поверхности нужно вычислять с помощью такого выражения:
Sпол = 2 π * r 2 + х * Р.
Видео:Тема 4. Цилиндр. Осевое сечение цилиндра. Развертка боковой поверхности цилиндра. Площадь боковойСкачать

Чему равны некоторые сечения прямого кругового цилиндра?
Когда сечение проходит через ось, то его площадь определяется как произведение образующей и диаметра основания. Это объясняется тем, что оно имеет вид прямоугольника, стороны которого совпадают с обозначенными элементами.
Читайте также: Как посчитать объем цилиндра в см3 калькулятор
Чтобы найти площадь сечения цилиндра, являющегося параллельным осевому, потребуется тоже формула для прямоугольника. В этой ситуации одна его сторона будет по-прежнему совпадать с высотой, а другая равна хорде основания. Последняя же совпадает с линией сечения по основанию.
Когда сечение перпендикулярно оси, то оно имеет вид круга. Причем его площадь такая же, как у основания фигуры.
Возможно еще пересечение под некоторым углом к оси. Тогда в сечении получается овал или его часть.
Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Примеры задач
Задание №1. Дан прямой цилиндр, площадь основания которого 12,56 см 2 . Необходимо вычислить полную площадь цилиндра, если его высота равна 3 см.
Решение. Необходимо воспользоваться формулой для полной площади кругового прямого цилиндра. Но в ней не хватает данных, а именно радиуса основания. Зато известна площадь круга. Из нее легко вычислить радиус.
Он оказывается равным квадратному корню из частного, которое получается от деления площади основания на пи. После деления 12,56 на 3,14 выходит 4. Квадратный корень из 4 — это 2. Поэтому радиус будет иметь именно такое значение.
Теперь можно подсчитать площадь боковой поверхности. Для этого следует умножить пи на радиус, высоту и 2. Произведение будет выглядеть так: 3,14 * 3 * 2 * 2. Итогом действий является: 37,68 см 2 .
Для того чтобы сосчитать полную площадь нужно сложить два основания (12,56 см 2 ) и боковую поверхность (37,68 см 2 ). В результате получается число 50,24 см 2 .
Задание №2. Цилиндр с радиусом 5 см пресечен плоскостью, параллельной оси. Расстояние от сечения до оси равно 3 см. Высота цилиндра — 4 см. Требуется найти площадь сечения.
Решение. Форма сечения — прямоугольная. Одна его сторона совпадает с высотой цилиндра, а другая равна хорде. Если первая величина известна, то вторую нужно найти.
Для этого следует сделать дополнительное построение. В основании проводим два отрезка. Оба они будут начинаться в центре окружности. Первая будет заканчиваться в центре хорды и равняться известному расстоянию до оси. Вторая — на конце хорды.
Получится прямоугольный треугольник. В нем известны гипотенуза и один из катетов. Гипотенуза совпадает с радиусом. Второй катет равен половине хорды. Неизвестный катет, умноженный на 2, даст искомую длину хорды. Вычислим его значение.
Для того чтобы найти неизвестный катет, потребуется возвести в квадрат гипотенузу и известный катет, вычесть из первого второе и извлечь квадратный корень. Квадраты равны 25 и 9. Их разность – 16. После извлечения квадратного корня остается 4. Это искомый катет.
Хорда будет равна 4 * 2 = 8 (см). Теперь можно вычислить площадь сечения: 8 * 4 = 32 (см 2 ).
Задание №3. Необходимо вычислить площадь осевого сечения цилиндра. Известно, что в него вписан куб с ребром 10 см.
Решение. Осевое сечение цилиндра совпадает с прямоугольником, который проходит через четыре вершины куба и содержит диагонали его оснований. Сторона куба является образующей цилиндра, а диагональ основания совпадает с диаметром. Произведение этих двух величин даст площадь, которую нужно узнать в задаче.
Для поиска диаметра потребуется воспользоваться знанием того, что в основании куба – квадрат, а его диагональ образует равносторонний прямоугольный треугольник. Гипотенуза его является искомой диагональю фигуры.
Для ее расчета потребуется формула теоремы Пифагора. Нужно возвести в квадрат сторону куба, умножить ее на 2 и извлечь квадратный корень. Десять во второй степени — это сто. Умноженное на 2 — двести. Квадратный корень из 200 равен 10√2.
🎬 Видео
ЕГЭ. Математика. База . Задача 16.Площадь осевого сечения цилиндраСкачать

60. Площадь поверхности цилиндраСкачать

№543. Угол между диагоналями развертки боковой поверхности цилиндра равен φ, диагональ равна d.Скачать

Цилиндр - расчёт площади, объёма.Скачать

№ 1 - Геометрия 10-11 класс ПогореловСкачать

№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Объем цилиндра. Практическая часть. 11 класс.Скачать