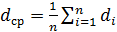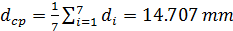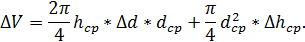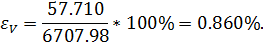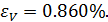Как найти работу цилиндра (3 видео)

Для изучения правильной обработки экспериментальных результатов и определения погрешностей прямых измерений проведём измерения диаметра и высоты цилиндра штангенциркулем.

а) Обработка результатов прямых измерений диаметра dцилиндра с помощью штангенциркуля.

1.Произведём7 измерений диаметра цилиндра в различных участках и результаты занесём в таблицу 2.

2.Найдем среднее значение диаметра цилиндра:

3.Определим среднюю квадратичную погрешность серии измерений по формуле (1):

4.Определим коэффициент Стьюдента (таблица 1) при надежности .

5.Найдём границы доверительного интервала по формуле (2):

Видео:КАК ПРОВЕРИТЬ РАБОТУ ЦИЛИНДРОВ ДВИГАТЕЛЯ с электронным бесконтактным зажиганиемСкачать

6. Вычислим относительную погрешность по формуле (3):

7.Запишем полученные результаты в виде:

8.Произведём7 измерений высоты цилиндра в различных участках и результаты занесём в таблицу 2.

9.Найдем среднее значение высоты цилиндра:

10.Определим среднюю квадратичную погрешность серии измерений по формуле:

Видео:Порядок работы цилиндров в рядном 4 цилиндровом двигателеСкачать

11.Определим коэффициент Стьюдента (таблица 1) при надежности .

12.Найдём границы доверительного интервала по формуле:

13. Вычислим относительную погрешность по формуле:

14.Запишем полученные результаты в виде:

Видео:Как быстро проверить работу цилиндров и бронепроводов! 2021Скачать

II. Определить объём цилиндра

С целью изучения обработки косвенных измерений, а они являются наиболее распространенными, требуется найти объём цилиндраV. Погрешность косвенных измерений зависит от погрешностей прямых измерений и вычисляется, в зависимости от вида функции, по формулам.

1.Проведём обработку измеренных значений диаметра и высоты цилиндра при одной и той же надежности .

2.Вычислим средний объём цилиндра:

3.Вычислим средний квадрат абсолютной погрешности объема:

4. Вычислим относительную погрешность объёма:

5. Запишем полученный результат в виде:

Видео:Говорю почему не работает один цилиндр двигателяСкачать

Таблица 1Значения коэффициента Стьюдента

nР	0,9	0,95	0,98	0,99
2	6,31	12,71	31,82	63,66
3	2,92	4,30	6,96	9,92
4	2,35	3,48	4,54	5,84
5	2,13	2,78	3,75	4,60
6	2,02	2,57	3,36	4,03
7	1,94	2,45	3,14	3,71
8	1,90	2,36	3,00	3,50
9	1,86	2,31	2,90	3,36
10	1,83	2,26	2,82	3,25

Таблица 2 — Результаты измерений диаметра и высоты цилиндра

Читайте также: Болт крепления рабочего цилиндра сцепления газель некст

n	d_i, мм	(d_i — d_ср) 2 , мм 2	h_i, мм	(h_i – h_ср) 2 , мм 2
1	15.00	0.0858	39.55	0.0018
2	14.75	0.0018	39.50	0.00049
3	14.75	0.0018	39.55	0.0018
4	14.60	0.011	39.60	0.0086
5	14.75	0.0018	39.60	0.0086
6	14.55	0.025	39.50	0.00049
7	14.55	0.025	39.25	0.066

Контрольные вопросы

1. Как измерить физическую величину.

2. Система единиц (основные и производные единицы измерения).

2. Виды измерений (прямые и косвенные).

4. Виды систематических ошибок.

5. Цель обработки результатов измерений прямых и косвенных.

6. Физический смысл коэффициента Стьюдента.

Содержание

Цилиндр, конус, шар
Цилиндр, конус, шар
Теорема Пифагора
🌟 Видео

Цилиндр, конус, шар

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям. Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

Основания цилиндра равны и лежат в параллельных плоскостях.
Все образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его основания ($R$).
Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.

Площадь поверхности и объем цилиндра.

Читайте также: Порядок работы цилиндров ваз 21099 инжектор

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.

Объем цилиндра равен произведению площади основания на высоту.

Объем части цилиндра, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.

Видео:Троит двигатель | Как определить, что не работает цилиндрСкачать

Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.

Распишем формулы объема цилиндра и шара.

Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.

Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.

Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.

Все образующие конуса равны.
Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.

Площадь поверхности и объем конуса.

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.

Объем конуса равен трети произведения площади основания на высоту.

Объем части конуса, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Читайте также: Не работает цилиндр двигателя приоры

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).

Тело, ограниченное сферой, называется шаром.

Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.

Площадь поверхности сферы: $S_ =4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы

Объем шара: $V= / = / $, где $R$ — радиус шара, $d$ — диаметр шара.

Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.

Теорема Пифагора

Видео:Нумерация цилиндров, как определить где какой номер цилиндра?/how to determine cylinder number?Скачать

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$ / $	$ / $	$ / $
$cosα$	$ / $	$ / $	$ / $
$tgα$	$ / $	$1$	$√3$
$ctgα$	$√3$	$1$	$ / $

Признаки подобия треугольников:

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.