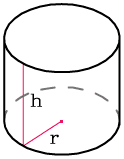
При вращении прямоугольника вокруг своей стороны получается геометрическое тело, называемое цилиндром. Данная геометрическая фигура ограничена цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями — основаниями цилиндра. Радиусом считается отрезок, соединяющий на плоскости основания точку центральной оси цилиндра с точкой его поверхности.
— Если известен объем и высота цилиндра, можно найти его радиус, как корень квадратный из объема деленного на произведение числа пи на высоту цилиндра:
- R = √V / πh
- S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2 =πr (2h+r)
- S (б.п.) = hP = 2πrh
- r = S (б.п.) / 2πh
- 2S (осн.) = πr 2
- r = √S (осн.) / π
- S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2
- Нахождение радиуса цилиндра: формула и примеры
- Формулы вычисления радиуса цилиндра
- 1. Через объем и высоту
- 2. Через площадь боковой поверхности
- 3. Через полную площадь поверхности
- Примеры задач
- Геометрические тела. Цилиндр.
- Формулы нахождения элементов цилиндра.
- Радиус и высота цилиндра
- Свойства
- Геометрические тела. Цилиндр.
- Формулы нахождения элементов цилиндра.
- Радиус и диагональ цилиндра
- Свойства
- Объем цилиндра
- Смотрите также
- 📺 Видео
R = √V / πh
где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:
S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2 =πr (2h+r)
Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:
S (б.п.) = hP = 2πrh
— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:
r = S (б.п.) / 2πh
Площадь двух оснований равна удвоенному произведению пи на радиус в квадрате:
2S (осн.) = πr 2
— Если известна площадь основания и высота, радиус находим как корень квадратный из площади одного основания деленного на пи:
r = √S (осн.) / π
S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2
где S (п.п.) — полная площадь поверхности цилиндра; r — радиус; h — высота.
Видео:Видеоурок по математике "Цилиндр"Скачать
Нахождение радиуса цилиндра: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.
Видео:Цилиндр - расчёт площади, объёма.Скачать
Формулы вычисления радиуса цилиндра
1. Через объем и высоту
Радиус цилиндра рассчитывается по формуле:
V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.
- R – радиус основания цилиндра, т.е. окружности;
- π – число, округленное значение которого равняется 3,14.
2. Через площадь боковой поверхности
Радиус цилиндра считается таким образом:
Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:
3. Через полную площадь поверхности
Данная формула получена следующим образом:
S – полная площадь поверхности фигуры, равная:
S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)
Возьмем первое выражение. Если перенести S в правую часть, получим:
2 π R 2 + 2 π Rh – S = 0
Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:
R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:
Читайте также: Объем наклонного цилиндра формула
* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать
Примеры задач
Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:
Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.
Решение:
Применим формулу, в которой задействованы заданные величины:
Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.
Решение:
Используем третью формулу для нахождения неизвестной величины:
Видео:Радиус и диаметрСкачать
Геометрические тела. Цилиндр.
Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.
ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.
Цилиндрические сечения боковой поверхности кругового цилиндра.
Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.
Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.
Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.
Круговой цилиндр – цилиндр, основанием которого является круг.
Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.
Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.
Призма – это частный случай цилиндра.
Видео:Объем цилиндраСкачать
Формулы нахождения элементов цилиндра.
Площадь боковой поверхности прямого кругового цилиндра:
Площадь полной поверхности прямого кругового цилиндра:
Объем прямого кругового цилиндра:
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.
Площадь боковой поверхности скошенного цилиндра:
Площадь оснований скошенного цилиндра:
Площадь полной поверхности скошенного цилиндра:
Объем скошенного цилиндра:
Sбок — площадь боковой поверхности;
Видео:КАК НАЙТИ ОБЪЕМ ШАРА, ЕСЛИ ИЗВЕСТЕН РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать
Радиус и высота цилиндра
Видео:Объём цилиндраСкачать
Свойства
Зная радиус цилиндра r, можно сразу найти его диаметр D и периметр окружности P, лежащей в его основании. Диаметр цилиндра является величиной в два раза большей радиуса по значению, а периметр окружности равен произведению диаметра на число π. D=2r P=2πr
Зная радиус и высоту цилиндра можно вычислить все необходимые параметры, такие как, например, площадь поверхности цилиндра или его объем, диагональ цилиндра и так далее. Площадь поверхности цилиндра может быть полной или только боковой, разница заключается в том, что для полной поверхности необходимо прибавить к боковой еще два основания. S_(б.п.)=hP=2πrh S_(п.п.)=S_(б.п.)+2S_(осн.)=2πrh+πr^2=πr(2h+r)
Объем цилиндра равен произведению его площади основания на высоту, то есть произведению числа π на высоту и квадрат радиуса. V=πr^2 h
Чтобы найти диагональ цилиндра, необходимо провести диаметр в основании таким образом, чтобы он соединял диагональ с высотой цилиндра, расположенной на его боковой поверхности. Тогда из образованного прямоугольного треугольника, можно вычислить диагональ цилиндра через радиус и высоту цилиндра по теореме Пифагора. (рис.25.1) d=√(D^2+h^2 )=√(4r^2+h^2 )
В цилиндр можно вписать сферу только тогда, когда диаметр его основания равен его высоте. То же самое касается и сферы описанной вокруг цилиндра. Радиус вписанной в цилиндр сферы равен радиусу окружности, лежащей в основании сферы, или половине высоты, а радиус сферы описанной около цилиндра равен половине его диагонали. (рис.25.2, 25.3) r_1=r=h/2 R=d/2=√(4r^2+h^2 )/2
Видео:11 класс. Геометрия. Объем цилиндраСкачать
Геометрические тела. Цилиндр.
Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.
ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.
Цилиндрические сечения боковой поверхности кругового цилиндра.
Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.
Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.
Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.
Круговой цилиндр – цилиндр, основанием которого является круг.
Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.
Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.
Призма – это частный случай цилиндра.
Видео:ОБЪЕМ ЦИЛИНДРА #shorts #егэ #огэ #математика #профильныйегэСкачать
Формулы нахождения элементов цилиндра.
Площадь боковой поверхности прямого кругового цилиндра:
Площадь полной поверхности прямого кругового цилиндра:
Объем прямого кругового цилиндра:
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.
Площадь боковой поверхности скошенного цилиндра:
Площадь оснований скошенного цилиндра:
Площадь полной поверхности скошенного цилиндра:
Объем скошенного цилиндра:
Sбок — площадь боковой поверхности;
Видео:Длина окружности. Математика 6 класс.Скачать
Радиус и диагональ цилиндра
Видео:Объем цилиндра.Скачать
Свойства
Через радиус цилиндра можно найти его диаметр и периметр окружности, которая находится в основании цилиндра, не прибегая к дополнительным вычислениям. Чтобы найти диаметр цилиндра, нужно умножить его радиус на два, а чтобы найти периметр окружности, нужно его умножить на два числа π. D=2r P=2πr
Чтобы узнать все остальные параметры цилиндра, необходимо сначала найти высоту. Через диагональ цилиндра это можно сделать, построив с высотой прямоугольный треугольник, и составив в нем теорему Пифагора. (рис.25.1) h=√(d^2-D^2 )
Площадь боковой и полной поверхности зависит от высоты и радиуса цилиндра, но можно также найти площадь цилиндра через радиус и диагональ. Для этого вместо высоты впишем в формулу квадратный корень из разности квадрата диагонали и четырех квадратов радиуса. S_(б.п.)=hP=2πrh=2πr√(d^2-〖4r〗^2 ) S_(п.п.)=S_(б.п.)+2S_(осн.)=πr(2√(d^2-〖4r〗^2 )+r)
Объем цилиндра представлен обычно произведением площади его основания на высоту, но для того чтобы вычислить объем цилиндра через радиус и диагональ необходимо умножить число π на квадрат радиуса и квадратный корень, соответствующий высоте. V=πr^2 h=πr^2 √(d^2-〖4r〗^2 )
Радиус сферы, которую можно вписать в цилиндр, должен быть равен радиусу самого цилиндра – это непременное условие для возможности совмещения этих двух тел. Более того, в таком случае радиус цилиндра должен быть ровно в два раза меньше его высоты, чтобы вписанная сфера соприкасалась не только с боковой поверхностью цилиндра, но и основаниями. (рис. 25.2) r_1=r
Условия для сферы, описанной около цилиндра, совпадают с условиями для вписанной сферы. При их соблюдении радиус сферы становится равным половине диагонали цилиндра. (рис.25.3) R=d/2
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать
Объем цилиндра
Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.
Если вам необходимо вычислить объем цилиндра, то прежде, чем начать его вычисление отставьте прочь калькуляторы и свои методы решения. Ведь теперь у вас есть более легкий способ решить такую задачу, а именно наш онлайн калькулятор, который сэкономит ваше время и лишит возможности ошибиться. Все что от вас требуется это ввести несколько значений. Причем мы предлагаем два способа решения с любым из неизвестных.
Первый способ наш онлайн калькулятор вычисляет по формуле: , а второй по формуле
Где S – это площадь основания, h – это высота цилиндра, число пи равное 3.14159, а r— это радиус цилиндра.
Смотрите также
Спасибо, очень полезным оказался
Спасибо, очень удобный калькулятор. Вспомнила формулу вычисления объёма. Невозможно держать в голове всю школьную программу. Пользуешься только необходимыми вычислениями, которые нужны для моей профессии.
А в каких единицах измерения, в бананах или коровах? Услугами данного калькулятора пользуются не профессора! Бесполезно потраченное время!
Оксана, результат у тебя, и таких как ты, получится в кубических курах. Потому, что у вас мозги куриные!
В школу ходить надо было.
Если измерение проводится в см, то и получаете см возведённые в куб.
Учитель не до конца вам объяснил или вы не усвоили, что в геометрии как правило объем измеряется в кубах, соответственно:
— Если вводите в бананах, то результат будет в бананах кубических,
— Если в сантиметрах, то результат будет в сантиметрах кубических (см³).
и т.д.
Слушайте учителей, образовывайтесь, заставляйте свой мозг работать.
Не нужно быть профессором чтобы воспользоваться этим калькулятором
Разницы нету метры, сантимеры, миллиметры он вам выдаёт куб того что вы ввели.
📺 Видео
Окружность. Как найти Радиус и ДиаметрСкачать
№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать
Длина окружности. Площадь круга - математика 6 классСкачать
Егэ.11кл. Объём первого цилиндра равен 12 м³, у второго цилиндра высота в 3 раза больше,а основаниеСкачать
Длина окружности. Площадь круга. 6 класс.Скачать
Геометрия Цилиндр описан около шара. Найдите объем шара, если известно, что объем цилиндра равен 60.Скачать
Задачи на цилиндр. Объем цилиндра - bezbotvyСкачать
Объем цилиндра. Практическая часть. 11 класс.Скачать
