Как найти радиус в цилиндре не имея объема

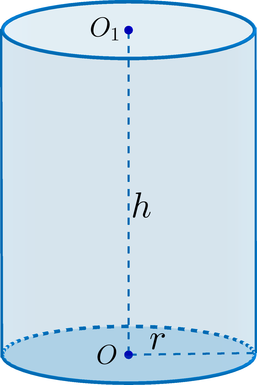
При вращении прямоугольника вокруг своей стороны получается геометрическое тело, называемое цилиндром. Данная геометрическая фигура ограничена цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями — основаниями цилиндра. Радиусом считается отрезок, соединяющий на плоскости основания точку центральной оси цилиндра с точкой его поверхности.

— Если известен объем и высота цилиндра, можно найти его радиус, как корень квадратный из объема деленного на произведение числа пи на высоту цилиндра:

R = √V / πh

где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2 =πr (2h+r)

Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:

S (б.п.) = hP = 2πrh

— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:

r = S (б.п.) / 2πh

Площадь двух оснований равна удвоенному произведению пи на радиус в квадрате:

2S (осн.) = πr 2

— Если известна площадь основания и высота, радиус находим как корень квадратный из площади одного основания деленного на пи:

r = √S (осн.) / π

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2

где S (п.п.) — полная площадь поверхности цилиндра; r — радиус; h — высота.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Нахождение радиуса цилиндра: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.

Видео:Объём цилиндраСкачать

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.

• R – радиус основания цилиндра, т.е. окружности;
• π – число, округленное значение которого равняется 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

3. Через полную площадь поверхности

Данная формула получена следующим образом:

S – полная площадь поверхности фигуры, равная:

S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)

Возьмем первое выражение. Если перенести S в правую часть, получим:

2 π R 2 + 2 π Rh – S = 0

Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:

R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:

* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.

Видео:Цилиндр - расчёт площади, объёма.Скачать

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

Видео:Видеоурок по математике "Цилиндр"Скачать

Нахождение радиуса вписанного в цилиндр шара (сферы)

В данной публикации мы рассмотрим, чему равняется радиус вписанного в прямой цилиндр шара или сферы. Информация сопровождается рисунками для лучшего восприятия.

Читайте также: Теплоизолированный цилиндр расположенный горизонтально 300 900

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Нахождение радиуса шара/сферы

Радиус зависит от того, как именно шар (сфера) вписан в цилиндр. Сделать это можно тремя способами:

1. Шар/сфера касается обоих оснований и боковой поверхности цилиндра

2. Шар/сфера касается только оснований цилиндра

Радиус (R) составляет половину высоты (h) цилиндра.

3. Шар/сфера касается только боковой поверхности цилиндра

В данном случае радиус (R) шара равняется радиусу (R) оснований цилиндра.

Примечание: еще раз подчеркнем, что вышеизложенная информация применима только к прямому цилиндру.

Видео:Объем цилиндра.Скачать

Радиус и высота цилиндра

Видео:Объем цилиндраСкачать

Свойства

Зная радиус цилиндра r, можно сразу найти его диаметр D и периметр окружности P, лежащей в его основании. Диаметр цилиндра является величиной в два раза большей радиуса по значению, а периметр окружности равен произведению диаметра на число π. D=2r P=2πr

Зная радиус и высоту цилиндра можно вычислить все необходимые параметры, такие как, например, площадь поверхности цилиндра или его объем, диагональ цилиндра и так далее. Площадь поверхности цилиндра может быть полной или только боковой, разница заключается в том, что для полной поверхности необходимо прибавить к боковой еще два основания. S_(б.п.)=hP=2πrh S_(п.п.)=S_(б.п.)+2S_(осн.)=2πrh+πr^2=πr(2h+r)

Объем цилиндра равен произведению его площади основания на высоту, то есть произведению числа π на высоту и квадрат радиуса. V=πr^2 h

Чтобы найти диагональ цилиндра, необходимо провести диаметр в основании таким образом, чтобы он соединял диагональ с высотой цилиндра, расположенной на его боковой поверхности. Тогда из образованного прямоугольного треугольника, можно вычислить диагональ цилиндра через радиус и высоту цилиндра по теореме Пифагора. (рис.25.1) d=√(D^2+h^2 )=√(4r^2+h^2 )

В цилиндр можно вписать сферу только тогда, когда диаметр его основания равен его высоте. То же самое касается и сферы описанной вокруг цилиндра. Радиус вписанной в цилиндр сферы равен радиусу окружности, лежащей в основании сферы, или половине высоты, а радиус сферы описанной около цилиндра равен половине его диагонали. (рис.25.2, 25.3) r_1=r=h/2 R=d/2=√(4r^2+h^2 )/2

Видео:Длина окружности. Математика 6 класс.Скачать

Радиус и объем цилиндра

Видео:Найти радиус основания цилиндраСкачать

Свойства

Периметр основания цилиндра через радиус может быть выражен как удвоенное произведение его на число π, или как произведение диаметра на число π, поскольку диаметр окружности равен двум радиусам. D=2r P=2πr

Зная радиус и объем цилиндра, можно найти его высоту, разделив объем на произведение квадрата радиуса и числа π. h=V/(πr^2 )

Площадь боковой и полной поверхности цилиндра можно найти через радиус и высоту, или через радиус и объем за неимением высоты. Площадь боковой поверхности цилиндра равна отношению удвоенного объема к двум радиусам. Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и двух площадей основания, то есть произведения числа π на квадрат радиуса цилиндра. S_(б.п.)=hP=2πrh=2πr V/(πr^2 )=2V/r S_(п.п.)=S_(б.п.)+2S_(осн.)=2V/r+πr^2

Диагональ цилиндра можно вычислить по теореме Пифагора из прямоугольного треугольника, который образован диаметром окружности в основании цилиндра и высотой цилиндра. (рис.25.1) d=√(D^2+h^2 )=√(4r^2+h^2 )=√(4r^2+(V/(πr^2 ))^2 )=√(4r^2+V^2/(π^2 r^4 ))

Если диаметр окружности, лежащей в основании цилиндра, равен его высоте, то в такой цилиндр можно вписать сферу, или описать сферу вокруг него. Радиус сферы, вписанной в цилиндр, равен радиусу самого цилиндра, так как окружность вращения сферы совпадает по размерам с окружность в основании цилиндра. Радиус сферы, описанной вокруг цилиндра, равен половине диагонали, так как сфера пересекается с цилиндром именно в точках, являющихся вершинами диагоналей, следовательно, последние совпадают с диаметром сферы. (рис.25.2,25.3) r_1=r R=d/2=√(4r^2+V^2/(π^2 r^4 ))/2

Видео:Высота второго цилиндра в три раза больше, а радиус в два раза меньше, чем у первого. Найти объемСкачать

Радиус и диагональ цилиндра

Видео:Радиус и диаметрСкачать

Свойства

Через радиус цилиндра можно найти его диаметр и периметр окружности, которая находится в основании цилиндра, не прибегая к дополнительным вычислениям. Чтобы найти диаметр цилиндра, нужно умножить его радиус на два, а чтобы найти периметр окружности, нужно его умножить на два числа π. D=2r P=2πr

Чтобы узнать все остальные параметры цилиндра, необходимо сначала найти высоту. Через диагональ цилиндра это можно сделать, построив с высотой прямоугольный треугольник, и составив в нем теорему Пифагора. (рис.25.1) h=√(d^2-D^2 )

Читайте также: Прямоугольный параллепипед описанный около цилиндра

Площадь боковой и полной поверхности зависит от высоты и радиуса цилиндра, но можно также найти площадь цилиндра через радиус и диагональ. Для этого вместо высоты впишем в формулу квадратный корень из разности квадрата диагонали и четырех квадратов радиуса. S_(б.п.)=hP=2πrh=2πr√(d^2-〖4r〗^2 ) S_(п.п.)=S_(б.п.)+2S_(осн.)=πr(2√(d^2-〖4r〗^2 )+r)

Объем цилиндра представлен обычно произведением площади его основания на высоту, но для того чтобы вычислить объем цилиндра через радиус и диагональ необходимо умножить число π на квадрат радиуса и квадратный корень, соответствующий высоте. V=πr^2 h=πr^2 √(d^2-〖4r〗^2 )

Радиус сферы, которую можно вписать в цилиндр, должен быть равен радиусу самого цилиндра – это непременное условие для возможности совмещения этих двух тел. Более того, в таком случае радиус цилиндра должен быть ровно в два раза меньше его высоты, чтобы вписанная сфера соприкасалась не только с боковой поверхностью цилиндра, но и основаниями. (рис. 25.2) r_1=r

Условия для сферы, описанной около цилиндра, совпадают с условиями для вписанной сферы. При их соблюдении радиус сферы становится равным половине диагонали цилиндра. (рис.25.3) R=d/2

Видео:11 класс, 32 урок, Объем цилиндраСкачать

Нахождение радиуса/площади/объема описанной вокруг цилиндра сферы (шара)

В данной публикации мы рассмотрим, как найти радиус описанной вокруг прямого цилиндра сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Нахождение радиуса сферы/шара

Около любого цилиндра можно описать сферу (или другими словами, вписать цилиндр в шар) – но только одну.

Центром такой сферы будет являться центр цилиндра, в нашем случае – это точка O.

Можно заметить, что радиус описанной сферы (OE), половина высоты цилиндра (OO₁) и радиус его основания (O₁E) образовывают прямоугольный треугольник OO₁E.

Воспользовавшись теоремой Пифагора мы можем найти гипотенузу этого треугольника, которая одновременно является радиусом сферы, описанной около заданного цилиндра:

Зная радиус сферы можно вычислить площадь (S) ее поверхности и объем (V) ограниченного сферой шара:

Примечание: π округленно равняется 3,14.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Задачи на тему «Цилиндр»

\(\blacktriangleright\) Ось цилиндра – прямая, соединяющая центры его оснований.
Отрезок, соединяющий центры оснований – высота.

\(\blacktriangleright\) Образующая цилиндра – перпендикуляр, проведенный из точки границы одного основания к другому основанию.
Заметим, что образующая и высота цилиндра равны друг другу.

\(\blacktriangleright\) Площадь боковой поверхности цилиндра \( >=2\pi rh>>\) , где \(r\) – радиус основания, \(h\) – высота (или образующая).

\(\blacktriangleright\) Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований. \[ >=2\pi rh+2\pi r^2>>\]

\(\blacktriangleright\) Объем цилиндра \( >\cdot h=\pi r^2h>>\)

Заметим, что прямой цилиндр имеет некоторое сходство с прямой призмой, только в ее основаниях лежат многоугольники (граница которых – ломаная), а в основаниях цилиндра – круги (граница которых гладкая).
Поэтому можно сказать, что боковая поверхность прямой призмы “ребристая”, а цилиндра – “гладкая”.

Про прямые круговые цилиндры \(C_1\) и \(C_2\) известно, что у \(C_1\) радиус основания в два раза больше, чем у \(C_2\) , но у \(C_2\) высота в три раза больше, чем у \(C_1\) . Найдите отношение объёма цилиндра \(C_2\) к объёму \(C_1\) .

Обозначим высоту цилиндра \(C_1\) через \(h_1\) , а высоту цилиндра \(C_2\) через \(h_2\) . Обозначим радиус основания цилиндра \(C_1\) через \(r_1\) , а радиус основания цилиндра \(C_2\) через \(r_2\) . Тогда \[r_1 = 2r_2,\qquad h_2 = 3h_1\,.\]

Объём цилиндра \(C_1\) равен \(\pi ^2 h_1 = 4\pi ^2 h_1\) , а объём цилиндра \(C_2\) равен \(3\pi ^2 h_1\) , тогда \[\dfrac > > = \dfrac ^2 h_1> ^2 h_1> = 0,75\]

Объем цилиндра равен \(64\pi\) , а площадь боковой поверхности равна \(32\pi\) . Найдите площадь полной поверхности цилиндра, деленную на \(\pi\) .

Формулы для нахождения объема и боковой поверхности цилиндра: \(V = \pi R^2 h\) , \(S_ > = 2\pi R h\) . Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: \[\frac >> = \frac = \frac = \frac = 2\] \(\Rightarrow\) \(R = 4\) . Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований: \[S_ > = 2\pi R h + 2 \pi R^2 = 32\pi + 2 \cdot 16\pi = 64\pi.\] Осталось разделить полученный объем на \(\pi\) , тогда окончательно получаем \(64\) .

Читайте также: Пыльник тормозного цилиндра газель некст

Объем цилиндра равен \(100\pi\) , а площадь боковой поверхности равна \(25\pi\) . Найдите высоту цилиндра.

Формулы для нахождения объема и боковой поверхности цилиндра: \(V = \pi R^2 h\) , \(S_ > = 2\pi R h\) . Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: \[\frac >> = \frac = \frac = \frac = 4\] \(\Rightarrow\) \(R = 8\) . Подставим значение радиуса в формулу объема и найдем из этой формулы искомую высоту: \[V = \pi R^2 h = 64\pi h = 100\pi\] \(\Rightarrow\) \(\displaystyle h = \frac = 1,5625\) .

Объём цилиндра \[V = \dfrac >,\] а отношение радиуса его основания к его высоте равно \(5\) . Найдите площадь полной поверхности этого цилиндра.

\[V_ > = \pi R^2 H = \dfrac >,\] \(\dfrac = 5\) , где \(R\) – радиус основания цилиндра, \(H\) – его высота, тогда \(R = 5H\) , следовательно, \[\pi \cdot 25 H^3 = \dfrac >\qquad\Rightarrow\qquad H^3 = \dfrac >,\] откуда \(H = \dfrac >\) , \(R = \dfrac >\) . \[S_ > = 2\pi R H + \pi R^2 = 2\pi R(H + R) = 2\pi\cdot\dfrac >\cdot\dfrac > = 240.\]

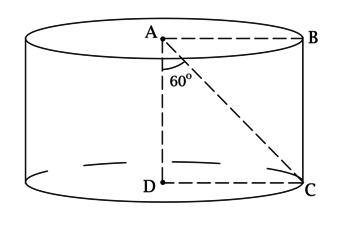
\(AD\) – ось цилиндра, \(BC\) – его образующая, \(S_ = \dfrac > >\) , \(\angle CAD = 60^\circ\) . Найдите объём цилиндра.

Так как \(AD\) и \(BC\) – высоты цилиндра, то \(ABCD\) – прямоугольник, тогда \[S_ = AD\cdot DC = H\cdot R = \dfrac > >.\]

Рассмотрим прямоугольный треугольник \(ADC\) :
Т.к. \(\angle DAC = 60^\circ\) , то \[AD = \mathrm \, \angle ACD\cdot DC = \mathrm \, 30^\circ\cdot R = \dfrac >,\] т.е. \(H = \dfrac >\) или \(R = \sqrt H\) .

Повторение базовой теории и формул, в том числе и тех, которые позволяют выполнить расчет объема цилиндра, — один из основных этапов подготовки к ЕГЭ. Несмотря на то, что эта тема достаточно подробно рассматривается на уроках математики в школе, с необходимостью вспомнить основной материал и «прокачать» навык решения задач сталкиваются многие учащиеся. Понимая, как вычислить объем и другие неизвестные параметры цилиндра, старшеклассники смогут получить достаточно высокие баллы по итогам сдачи единого государственного экзамена.

Видео:🔴 Даны два цилиндра. Радиус основания и высота ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Основные нюансы, которые стоит вспомнить

Чтобы вопрос, как посчитать объем цилиндра и выполнить измерение других неизвестных параметров при решении задач, не ставил ученика в тупик, рекомендуем повторить основные свойства этой фигуры прямо сейчас в режиме онлайн.

• Цилиндр представляет собой тело, которое ограничено цилиндрической поверхностью и двумя кругами. Цилиндрическая поверхность является боковой. А круги представляют собой основания фигуры.
• Высота цилиндра есть расстояние между плоскостями его оснований.
• Все его образующие являются параллельными и равными между собой.
• Радиус цилиндра есть радиус его основания.
• Фигура называется прямой, если ее образующие перпендикулярны основаниям.

Видео:Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать

Как подготовиться к экзамену качественно и эффективно?

Занимаясь накануне прохождения аттестационного испытания, многие учащиеся сталкиваются с проблемой поиска необходимой информации. Далеко не всегда школьный учебник оказывается под рукой, когда это требуется. А найти формулы, которые помогут рассчитать площадь и другие неизвестные параметры цилиндра, часто бывает достаточно сложно даже в Интернете в онлайн-режиме.

Занимаясь вместе с математическим порталом «Школково», выпускники смогут избежать типовых ошибок и успешно сдать единый госэкзамен. Мы предлагаем выстроить процесс подготовки по-новому, переходя от простого к сложному. Это позволит учащимся определить непонятные для себя тематики и ликвидировать пробелы в знаниях.

Весь базовый материал, который поможет в решении задач на тему «Цилиндр», выпускники смогут найти в разделе «Теоретическая справка». Специалисты «Школково» изложили с доступной форме все необходимые определения и формулы.

Для закрепления полученных знаний учащиеся могут попрактиковаться в решении задач на тему «Цилиндр» и другие темы, например, нахождение площади или объема конуса. Большая, постоянно обновляющаяся подборка заданий представлена в разделе «Каталог».

Чтобы во время подготовки к ЕГЭ быстро найти конкретную задачу по теме «Цилиндр» и освежить в памяти алгоритм ее решения, выпускники могут предварительно сохранить ее в «Избранное». Отрабатывать собственные навыки на нашем сайте имеют возможность не только столичные школьники, но и учащиеся из других российских городов.

📺 Видео

Объем цилиндра.Скачать

ЕГЭ-2020: Изменение объёма цилиндраСкачать

ПЛОЩАДЬ боковой поверхности ЦИЛИНДРАСкачать

Объем шара и цилиндра. Практическая часть. 11 класс.Скачать