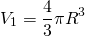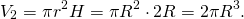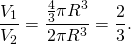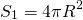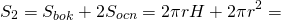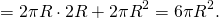Как найти радиус вписанной сферы в цилиндр (2 видео)

@ Часто встречаются и представляют интерес задачи, в которых взаимодействуют тела вращения с телами вращения и многогранниками.

Сфера называется описанной около цилиндра (конуса), если окружности его оснований (окружность его основания и вершина) принадлежат сфере.

Около любого цилиндра и любого конуса можно описать сферу.

Сфера называется вписанной в цилиндр , если она касается каждой образующей и обоих оснований цилиндра.

В цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания.

Центр сферы является серединой отрезка, соединяющего центры оснований.

Сфера называется вписанной в конус , если она касается образующих конуса и его основания.

В любой конус можно вписать сферу.

Сфера называется вписанной в усеченный конус , если она касается всех образующих и обоих оснований конуса.

Очевидно справедливо утверждение: в усеченный конус можно вписать сферу тогда и только тогда, когда образующая усеченного конуса равна сумме радиусов оснований. Тогда диаметр сферы равен высоте усеченного конуса.

Понятия вписанная и описанная сферы и вписанный и описанный шары в задачах не различаются.

Цилиндр называется вписанным в конус , если одно его основание принадлежит основанию конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию.

Основание цилиндра и основание конуса – концентрические круги.

Во всякий конус можно вписать цилиндр. Его высота меньше высоты конуса.

Цилиндр называется вписанным в усеченный конус , если одно его основание принадлежит основанию конуса, а другое совпадает со вторым основанием конуса. Высота такого цилиндра равна высоте усеченного конуса.

Так как цилиндр и конус однозначно определяются двумя независимыми параметрами, то, задав два независимых параметра одной фигуры и один параметр другой (вписанной или описанной), можно найти остальные параметры.

1 . В конус высоты Н и радиуса R вписан цилиндр высоты h . Найти радиус основания цилиндра.

Шар задается однозначно одним параметром, поэтому, задав параметр шара и один из независимых параметров вписанного или описанного конуса или цилиндра, можно найти другой параметр.

Или же по двум независимым параметрам конуса или цилиндра можно определить параметр вписанного или описанного шара.

2. В конус высоты Н и радиуса R вписан шар. Найти радиус шара.

3. В усеченный конус, радиусы оснований которого R и r , вписан шар. Найти его радиус.

4. В шар радиуса R вписан цилиндр высоты Н . Найти радиус его основания.

Пример 7.6.2. (КубГУ, матем., 1971 г.)

В прямой конус с образующей 1 и углом 2 a при вершине осевого сечения вписан шар. Вычислить радиус окружности, по которой соприкасаются поверхности конуса и шара, а также объем и полную поверхность меньшей из частей шара, на которые он рассекается кругом упомянутого радиуса. Решение

Читайте также: Что такое цилиндр кале

Решение задач о вписанных телах вращения, как правило, сводится к планиметрическим. Поэтому сделаем чертеж осевого сечения конуса. Тогда сфера будет окружностью большого круга, вписанной в равнобедренный треугольник. Отрезок прямой, параллельной основанию, соединяющий точки касания окружности и треугольника, будет диаметром искомой окружности.

Из прямоугольного треугольника ACD имеем AD = 1 sin a .

АО – биссектриса угла CAD , следовательно, .

Из прямоугольного треугольника AOD находим , OD = OM как радиусы.

D MKO подобен D CMO , следовательно, KMO = a

Меньшая часть шара – шаровой сегмент, высота которого РК . Его объем и площадь поверхности вычисляются по формулам

Тогда PK = PO — OK . Подставив найденные величины и преобразовав, получим ,

Пример 7.6.3. (КубГУ, матем., 1979 г.)

Пример 7.6.4. (КубГУ, матем., 1986 г.)

В усеченный конус вписан шар, касающийся обоих оснований и боковой поверхности. Найти длину образующей усеченного конуса, если даны его высота h и радиус a окружности касания. Решение

Сделаем чертеж осевого сечения. Тогда MK = a , BP = h . Так как высота конуса равна диаметру шара, то . Р OMK = Р ABP , как острые углы со взаимно перпендикулярными сторонами. Тогда D OMK подобен D ABP и имеет место соотношение , откуда .

Ответ: .

Пример 7.6.5. (КубГУ, эконом., 1989 г.)

Пусть AC = a , тогда из чертежа осевого сечения находим CD = a tg a , .

Разделив обе части на , получим .

Из прямоугольного треугольника имеем , тогда

Пример 7.6.6. (КубГУ, матем., 1979 г.)

В усеченный конус вписан шар радиуса R . Образующая конуса наклонена к плоскости нижнего основания под углом ( a 90°) . Найти объем усеченного конуса. Решение

В шар радиуса R вписан конус. Угол между образующей конуса и плоскостью основания равен a . В конус вписан шар. Найти радиус вписанного шара. Решение

В осевом сечении конуса получили равнобедренный треугольник с вписанной и описанной окружностями. Отметим, что центры вписанной и описанной окружностей совпадают только у правильного треугольника. Если угол при вершине равнобедренного треугольника меньше 60° , то центр описанной окружности расположен на высоте ближе к этой вершине, чем центр вписанной окружности. Если треугольник прямоугольный, то центр описанной окружности совпадает с серединой гипотенузы, если же треугольник тупоугольный, то центр описанной окружности будет расположен вне треугольника, в то время как центр вписанной окружности для любого треугольника является внутренней точкой.

Если О – центр вписанной окружности, то АО биссектриса D CAD и из треугольника OAD находим .

Пример 7.6.8. (КубГУ, физич., 1979 г.)

Шар радиуса R вписан в конус. Из центра шара образующая конуса видна под углом a . Найти объем конуса. Решение

Пусть О – центр вписанной окружности в осевом сечении конуса. По условию Р AOC = a , тогда Р AOD = 180° — a . Очевидно, что a > 90° . Из прямоугольного треугольника AOD находим Р OAD = 180° — (90° + 180° -a) = a — 90° . АО – биссектриса Р CAD . Следовательно, Р CAD = 2 Р OAD = 2 a — 180° .
OD =R . Тогда из треугольника AOD находим AD. AD = OD tg AOD = R tg( 180° -a ) = — R tg a .

Из треугольника AСD находим СD

Подставив найденные величины в формулу объема, получим

Если 90° a 135° , то 180° a 270° ; тогда tg a , tg 2 a >0 и .

Если 135° a 180° , то 270° a 360° ; тогда tg 2 a , tg 2 a и .

Содержание

Сфера, описанная около цилиндра
Узнать ещё
Шар, вписанный в цилиндр
Нахождение радиуса/площади/объема описанной вокруг цилиндра сферы (шара)
Нахождение радиуса сферы/шара
Нахождение радиуса вписанного в цилиндр шара (сферы)
Нахождение радиуса шара/сферы
1. Шар/сфера касается обоих оснований и боковой поверхности цилиндра
2. Шар/сфера касается только оснований цилиндра
3. Шар/сфера касается только боковой поверхности цилиндра
📽️ Видео

Видео:Цилиндр, конус, шар, 6 классСкачать

Сфера, описанная около цилиндра

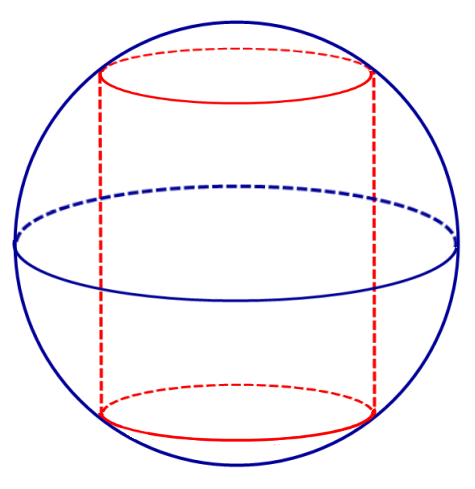
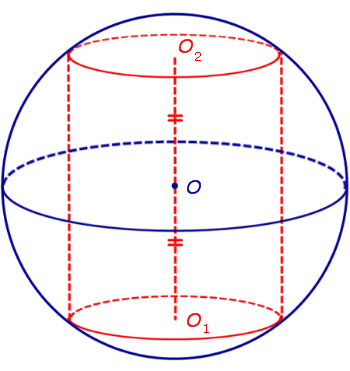
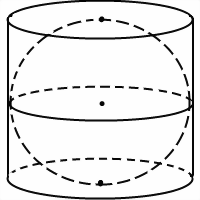
Определение 1. Цилиндром, вписанным в сферу, называют такой цилиндр, окружности оснований которого лежат на сфере (рис. 1).

Определение 2. Если цилиндр вписан в сферу, то сферу называют описанной около цилиндра.

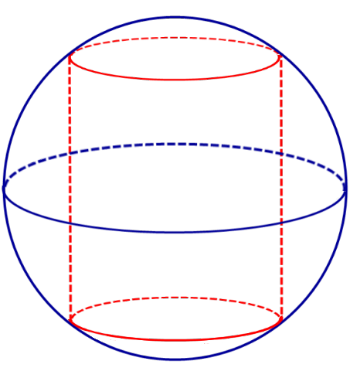
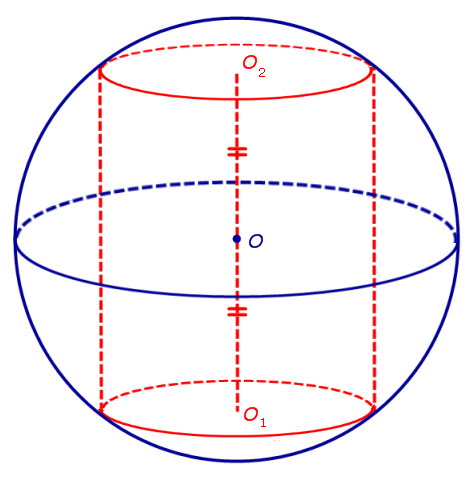
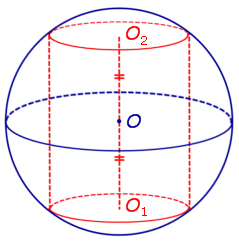
Утверждение. Около любого цилиндра можно описать сферу, причем только одну. Центр O этой сферы является серединой отрезка O₁O₂ , где O₁ и O₂ – центры оснований цилиндра (рис. 2)

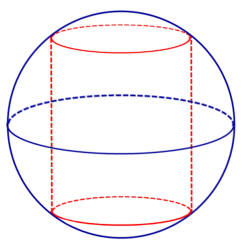
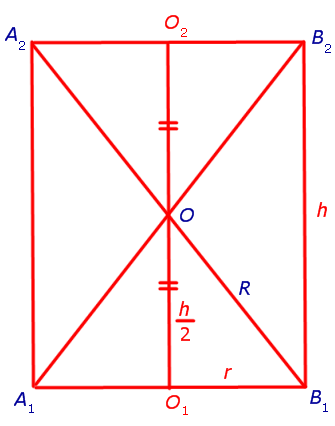
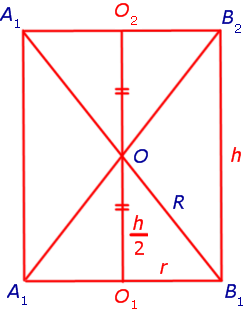
Доказательство. Обозначим буквами r и h радиус и высоту цилиндра и рассмотрим любое осевое сечение цилиндра (рис. 3).

Отрезки A₁A₂ и B₁B₂ , изображенные на рисунке 3, являются образующими цилиндра. Радиус R описанной сферы можно найти с помощью теоремы Пифагора из прямоугольного треугольника OB₁O₁ по формуле

Следствие 1. Радиус сферы, описанной около цилиндра с радиусом r и высотой h равен

Следствие 2. Отношение объема цилиндра к объему описанной около него сферы можно найти по формуле

Видео:Сфера и шар. Сечение сферы. Вписанная и описанная сфераСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Быстро находим радиус описанной сферыСкачать

Шар, вписанный в цилиндр

Шар, вписанный в цилиндр, касается оснований цилиндра в их центрах, а боковой поверхности цилиндра — по параллельной основаниям окружности большого круга (то есть радиус этой окружности равен радиусу шара).

Если шар вписан в цилиндр, то цилиндр описан около шара.

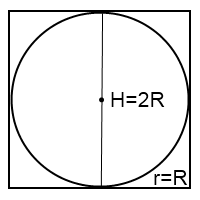
В цилиндр можно вписать шар тогда и только тогда, когда цилиндр равносторонний, то есть его высота равна диаметру. Радиус вписанного в цилиндр шара R равен радиусу цилиндра r:

Решение задач на шар, вписанный в цилиндр, чаще всего сводится к рассмотрению осевого сечения комбинации тел.

Это сечение представляет собой квадрат с вписанной в него окружностью. Сторона квадрата равна высоте цилиндра и диаметру шара:

Найдем отношение объема цилиндра к объему вписанного в него шара. Объем шара

Отсюда отношение объема шара к объему описанного около него цилиндра

Теперь найдем отношение площади поверхности цилиндра к площади вписанного шара. Площадь поверхности шара (площадь сферы)

Площадь полной поверхности цилиндра равна сумме площадей оснований и боковой поверхности:

Отсюда отношение площади поверхности вписанного шара к площади поверхности цилиндра

Видео:Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндраСкачать

Нахождение радиуса/площади/объема описанной вокруг цилиндра сферы (шара)

В данной публикации мы рассмотрим, как найти радиус описанной вокруг прямого цилиндра сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.

Видео:Окружность. Круг. 5 класс.Скачать

Нахождение радиуса сферы/шара

Около любого цилиндра можно описать сферу (или другими словами, вписать цилиндр в шар) – но только одну.

Можно заметить, что радиус описанной сферы (OE), половина высоты цилиндра (OO₁) и радиус его основания (O₁E) образовывают прямоугольный треугольник OO₁E.

Воспользовавшись теоремой Пифагора мы можем найти гипотенузу этого треугольника, которая одновременно является радиусом сферы, описанной около заданного цилиндра:

Зная радиус сферы можно вычислить площадь (S) ее поверхности и объем (V) ограниченного сферой шара:

Примечание: π округленно равняется 3,14.

Видео:Видеоурок по математике "Цилиндр"Скачать

Нахождение радиуса вписанного в цилиндр шара (сферы)

В данной публикации мы рассмотрим, чему равняется радиус вписанного в прямой цилиндр шара или сферы. Информация сопровождается рисунками для лучшего восприятия.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать