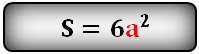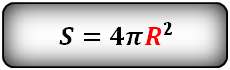Как найти sполн цилиндра

Видео:Цилиндр - расчёт площади, объёма.Скачать

Нахождение площади поверхности цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.

Видео:Видеоурок по математике "Цилиндр"Скачать

Формула вычисления площади цилиндра

1. Боковая поверхность

Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.

Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:

Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:

3. Полная площадь

Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:

S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .

Видео:60. Площадь поверхности цилиндраСкачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Все формулы для площадей полной и боковой поверхности тел

Видео:Объём цилиндраСкачать

1. Площадь полной поверхности куба

a — сторона куба

Формула площади поверхности куба,(S):

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

2. Найти площадь поверхности прямоугольного параллелепипеда

a , b , c — стороны параллелепипеда

Формула площади поверхности параллелепипеда, (S):

Видео:Как запомнить площадь поверхности цилиндра #математикапрофиль #геометрияегэСкачать

3. Найти площадь поверхности шара, сферы

R — радиус сферы

Формула площади поверхности шара (S):

Видео:Площадь полной поверхности цилиндраСкачать

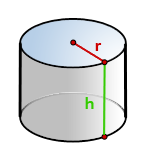
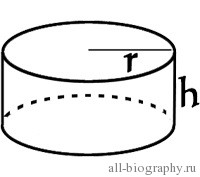
4. Найти площадь боковой и полной поверхности цилиндра

r — радиус основания

h — высота цилиндра

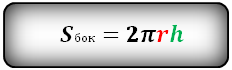
Формула площади боковой поверхности цилиндра, (S _бок ):

Формула площади всей поверхности цилиндра, (S):

Видео:Объем цилиндраСкачать

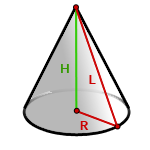
5. Площадь поверхности прямого, кругового конуса

R — радиус основания конуса

L — образующая конуса

Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S _бок ):

Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S _бок ):

Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):

Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):

Видео:Площадь поверхности призмы. 11 класс.Скачать

Площадь поверхности цилиндра

Всего получено оценок: 9327.

Всего получено оценок: 9327.

Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь поверхности цилиндра и, применив формулу, решим для примера несколько задач.

У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.

Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.

Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .

Видео:Нахождение площади боковой поверхности цилиндраСкачать

Боковая поверхность цилиндра

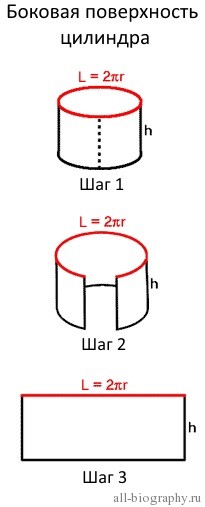
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).

После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.

Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.

Видео:Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндраСкачать

Площадь полной поверхности цилиндра

Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).

Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

Площадь боковой поверхности цилиндра равна 37,68.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

Площадь поверхности цилиндра равна 376,8.

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:

Значение радиуса получаем из формулы: d = 2r

Видео:Площадь сферы внутри цилиндра. Поверхностный интегралСкачать

Площадь поверхности цилиндра и его объем

Видео:Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шараСкачать

Площадь поверхности цилиндра

Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr, а высота равна высоте цилиндра h, т. е. 2πrh.

Полная поверхность цилиндра составит: 2πr 2 + 2πrh = 2πr (r + h).

За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.

Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле

где R — радиус основания, а H — высота цилиндра.

Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра

S_полн. =2πRH + 2πR 2 = 2πR (H + R).

Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Объем прямого цилиндра

где Q — площадь основания, а Н — высота цилиндра.

Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q_n и Q’_n таких, что

Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам

Следствие.
Объем прямого кругового цилиндра вычисляется по формуле

где R — радиус основания, а H — высота цилиндра.

Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому

Видео:11 класс, 32 урок, Объем цилиндраСкачать

Цилиндр

Вы будете перенаправлены на Автор24

Видео:Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать

Понятие цилиндра

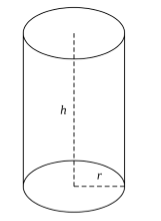
Геометрическая фигура, образованная двумя равными кругами, лежащими в параллельных плоскостях, все точки которых соединены между параллельными прямыми, так что никакая точка не остается несоединенной, называется цилиндром (рис. 1).

Круги при этом называются основаниями цилиндра, а прямые их соединяющие — образующими. Прямая, которая проходит через центры окружностей оснований называется осью цилиндра, а совокупность всех образующих — боковой поверхностью цилиндра.

Виды цилиндров

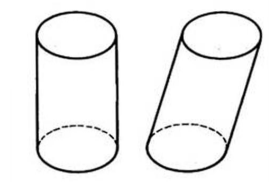
Цилиндр, у которого все образующие перпендикулярны к плоскостям, проходящим через основания, называется прямым. В противном же случае он является наклонным (рис. 2).

Рисунок 2. Прямой и наклонный цилиндры

Площадь поверхности цилиндра

Площадь поверхности цилиндра определяется следующим образом:

Найдем теперь формулы для вычисления площадь боковой поверхности и основания.

Так как в основании лежат круги, то очевидно, что

Площадь боковой поверхности цилиндра определяется как произведение длины окружности, ограничивающей основание цилиндра на его высоту.

Доказательство.

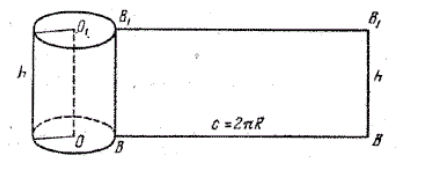
Для доказательства этой теоремы нам необходимо найти площадь развертки боковой поверхности цилиндра (рис. 3).

Видим, что разверткой боковой поверхности цилиндра является прямоугольник. Высота прямоугольника равняется высоте цилиндра $h$, а длина равняется длине окружности, ограничивающей основание цилиндра, то есть

Готовые работы на аналогичную тему

Теорема доказана.

Объем цилиндра

Объем цилиндра определяется как произведение площади основания цилиндра на его высоту.

Доказательство.

Рассмотрим цилиндр с радиусом $r$ и высотой $h$. Найдем ее объем $V$. Для этого сначала впишем в нее правильную $n-$угольную призму, в которую впишем еще один цилиндр. Пусть радиус второго цилиндра равняется $r’$, а её объем равен $V’$ (рис. 4).

Как мы знаем, объем призмы будет равен $S_ h$. Следовательно, получим следующую оценку

Теорема доказана.

Пример задачи

Найти площадь полной поверхности цилиндра и его объем, если радиус его основания равняется $7$ см, а высота в два раза больше диаметра основания.

Найдем вначале высоту цилиндра. Так как высота в два раза больше диаметра, получим

\[V=\pi r^2h=49\pi \cdot 28=1372\pi \]

Ответ: $490\pi ,\ 1372\pi $