Цилиндром будет называться геометрическое тело, полученное при ограничении цилиндрической поверхности двумя параллельными плоскостями — основаниями цилиндра. Если в основании цилиндра лежит окружность, а образующая перпендикулярна основанию, то цилиндр называется прямым круговым.
Линия сечения строится также при помощи опорных точек — точек пересечения секущей плоскости с очерковыми образующими и осью цилиндра. Но необходимо взять также промежуточные точки для более точного построения линии сечения. На рисунке 49 показано построение проекций сечения цилиндра фронтально — проецирующей плоскостью S. Так как цилиндр является проецирующей поверхностью, то горизонтальная проекция сечения совпадает с секущей плоскостью и на профильной проекции получим эллипс. Точки 2 и 3 будут являться границей видимости линии сечения для профильной плоскости.
Натуральную величину сечения можно определить способом вращения. Ось вращения выбираем в точке 1 и вращаем секущую плоскость до положения, параллельного горизонтальной плоскости. На горизонтальной плоскости получим эллипс, который будет являться натуральной величиной сечения цилиндра.
Разверткой цилиндра является прямоугольник с высотой, равной высоте цилиндра, и длиной, равной длине окружности основания 2πR. Для того, чтобы построить развертку усеченной части, основание цилиндра делят на равные части, тем самым аппроксимируя цилиндрическую поверхность призматической. Разделим окружность основания на 12 равных частей и отложим их вдоль горизонтальной линии развертки, по вертикали отложим высоту цилиндра (рис. 50).
Затем на полученных образующих отметим высоты точек сечения. Пристроим окружность основания и натуральную величину сечения.
Конус — это геометрическое тело, полученное путем ограничения конической поверхности плоскостью. Если в основании конуса лежит окружность, а высота попадает в центр основания, то конус называется прямым круговым.
На рисунке 51 построено сечение конуса фронтально — проецирующей плоскостью. Точки сечения находим при помощи вспомогательных секущих плоскостей. Точки С и D являются границей видимости для профильной проекции сечения.
Натуральную величину сечения находим способом вращения. Ось вращения выбираем в точке D и поворачиваем секущую плоскость до положения, параллельного горизонтальной плоскости проекций. Из горизонтальных проекций точек проводим линии, перпендикулярные оси вращения. Натуральной величиной сечения будет являться эллипс.
Развертка конуса является круговым сектором с радиусом, равным длине образующей конуса и длиной дуги, равной длине окружности основания конуса. Делим основание конуса на 12 равных частей и откладываем их по дуге на развертке. Затем на соответствующих образующих нужно отложить натуральные величины высот точек сечения. Чтобы получить полную развертку усеченной части, пристраиваем основание и натуральную величину сечения. На рисунке 52 показано построение развертки конуса.
1. Как образуется цилиндрическая поверхность?
2. Если секущая цилиндр плоскость фронтально проецирующая, то где будут лежать горизонтальные проекции точек сечения?
3. Какими способами можно определять натуральную величину фигуры сечения?
4. Какой геометрической фигурой является развертка боковой поверхности цилиндра? Конуса?
5. Для чего нужно разбивать окружность основания на некоторое количество равных частей?
6. Как построить развертку конической поверхности?
7. Как получить из полной развертки поверхности развертку ее усеченной части?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Видео:ЦИЛИНДР. Проекции точек на его поверхности. Достроить недостающие проекции точек на трех плоскостяхСкачать

Построение проекций точек, принадлежащих цилиндру и конусу
Пусть задана фронтальная проекция F2 точки F, принадлежащей боковой поверхности цилиндра вращения (рис. 164, а). Требуется построить три проекции точки F. Как известно, цилиндр вращения образуется путем вращения прямоугольника вокруг одной из его сторон, принимаемой за ось вращения. Противоположная сторона прямоугольника (образующая или производящая) образует при вращении боковую поверхность цилиндра; две другие стороны прямоугольника образуют верхнее и нижнее основания цилиндра, являющиеся кругами одного и того же диаметра.
Читайте также: 4gr fse расположение цилиндров
Поверхность цилиндра является в данном случае горизонтально-проецирующей поверхностью; следовательно, горизонтальная проекция F1 точки Р должна совпадать с горизонтальной проекцией боковой поверхности цилиндра (с окружностью).
Проекция F2 изображена светлым кружком; значит, точка F принадлежит передней поверхности цилиндра и спроецируется на нижнюю половину окружности в точку F1. Третью проекцию F3 строим с помощью ординаты у, откладывая ее размер вправо от оси z3.
При построении изометрического изображения удобно пользоваться видимым для нас верхним основанием цилиндра (рис. 164, б). Строим эллипс в плоскости х’О’у’, проводим касательные-к нему прямые— видимые образующие цилиндра — и нижний полуэллипс. Точку F’ находим с помощью координатной ломаной, что ясно из сравнения чертежей.
Пусть требуется построить три проекции точки G, принадлежащей поверхности конуса вращения (рис. 165, а).
Конус вращения образуется при вращении прямоугольного треугольника вокруг одного из его катетов. Гипотенуза прямоугольного треугольника является при этом образующей конуса. Верхняя точка образующей является вершиной конуса. Второй катет треугольника образует при вращении основание конуса. Судя по чертежу, вершина конуса расположена выше основания, поэтому вся боковая поверхность конуса будет видимой при проецировании на горизонтальную плоскость проекций П1; при проецировании на фронтальную плоскость проекций П2 видимой будет передняя половина боковой поверхности.
Фронтальная проекция G2 задана светлым кружком, т. е. точка G принадлежит передней поверхности конуса. Для построения горизонтальной проекции G1 существуют два способа: способ образующей и способ параллели. Рассмотрим способ образующей. Соединяем фронтальные проекции S2 и G2 прямой линией S2H2. Это будет фронтальная проекция образующей SH. Находим ее горизонтальную проекцию S1H1. Горизонтальную проекцию G1. искомой точки G находим, проведя вертикальную линию связи G2G1. Этот способ не дает точного результата в тех случаях, когда точка лежит вблизи передней образующей конуса. Более универсальным является второй способ — способ параллели. Он заключается в проведении через точку G окружности или параллели а. Ее фронтальная проекция а2 пересекает фронтальную проекцию левой образующей в точке А2. Находим точку А1 и радиусом А1S1 из центра S1 проводим окружность а1 — горизонтальную проекцию параллели а. Пересечение окружности с вертикальной линией связи определяет точку G1. Третью проекцию G3 находим с помощью ординаты у так же, как в предыдущей задаче; изображаем ее зачерненным кружком, поскольку точка G при проецировании на плоскость П3 невидимая.
Видео:Как начертить цилиндр в объемеСкачать

ЛИНЕЙНО-КОНСТРУКТИВНЫЙ РИСУНОК ЦИЛИНДРА
ЦЕЛЬ И ПОСТАНОВКА ЗАДАНИЯ. Научиться изображать цилиндр в перспективе.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ. Рассмотрите цилиндр на рис. 3.81 и его ортогональные проекции на рис. 3.82. Цилиндр – геометрическое тело, относящееся к так называемым телам вращения, т. е. цилиндр можно получить путем вращения прямоугольника вокруг одной из его сторон. Основаниями цилиндра являются окружности. Ось вращения цилиндра соединяет центры окружностей оснований и перпендикулярна им.
Приступая к рисунку вертикального цилиндра, сначала наметьте на листе вертикальную линию – ось цилиндра и перпендикулярные ей горизонтальные линии – большие оси эллипсов верхнего и нижнего оснований (рис. 3.83). Проведите вертикальные образующие цилиндра (рис. 3.84). Изображая эллипсы оснований, помните, что чем дальше находится основание от линии горизонта, тем больше его раскрытие. В нашем примере, когда цилиндр расположен ниже горизонта, раскрытие нижнего основания больше раскрытия верхнего основания цилиндра (рис. 3.85). Завершите рисунок, изобразив вертикальные сечения цилиндра двумя перпендикулярными плоскостями (рис. 3.86).
Последовательность изображения горизонтального цилиндра такая же, что и вертикального: наметьте ось цилиндра и перпендикулярные ей большие оси эллипсов оснований. Проведите образующие. Большая ось цилиндра и его образующие должны сходиться на линии горизонта в одну точку схода (рис. 3.87). Изобразите эллипсы оснований, учитывая, что большая ось ближнего к зрителю основания будет длиннее, чем большая ось дальнего основания, а раскрытие ближнего эллипса – меньше, чем раскрытие дальнего (рис. 3.88).
Читайте также: Цилиндр тормозной главный уаз патриот евро 4
Завершите рисунок, изобразив сечения цилиндра горизонтальной и вертикальными плоскостями (рис. 3.89). Если вашего опыта пока недостаточно, чтобы правильно найти направление оси цилиндра и раскрытие эллипсов оснований, вы можете воспользоваться рисунком куба. Вертикальные боковые грани куба задают габариты оснований цилиндра, горизонтальные ребра идут в одну точку схода с большой осью и образующими цилиндра, а также определяют его длину (рис. 3.90). Изображая цилиндр в произвольном положении, помните, что его ось вращения всегда перпендикулярна большим осям эллипсов оснований.
Видео:Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Ghenadie Sontu Fine Art
Видео:НАКЛОННЫЙ ЦИЛИНДР и недостающие проекции точек на его поверхности. Построить три проекции точек.Скачать

BLOG
Видео:Видеоурок по математике "Цилиндр"Скачать

Как рисовать цилиндр? Подробная инструкция рисования цилиндра.
Цилиндр — геометрическое тело, форма которого состоит из трех поверхностей: двух одинаковых по форме плоских кругов и одной, образующей форму, цилиндрической поверхности. Для того чтобы лучше разобраться и понять конструктивную основу строения формы цилиндра, в качестве наглядного пособия рассмотрим его каркасную модель. Изготовить такую модель-каркас не составляет труда. Для этого можно использовать проволоку — алюминиевую, медную, стальную или из мягкого сплава. Длина большой стороны каркаса может быть в пределах 7-10 см.
Изучение в рисунке каркасных моделей позволяет студентам лучше освоить конструктивную сущность предмета, его взаимосвязь и пространственность формы.
Рис.49. Перспективное построение окружностей оснований цилиндра: а — с одной точкой схода; б — с двумя точками схода
Изображение геометрического тела, расположенного на горизонтальной плоскости в обычном вертикальном положении, следует начинать с построения его основания. Как видно, на основаниях цилиндра имеются круглые по форме поверхности, ограниченные окружностью. С окружностью мы уже ознакомились и знаем методы и способы ее построения на плоскости. Основываясь на методе линейно-конструктивного построения изображения каркасных моделей, следует перейти к рассмотрению изображения цилиндра.
Изображение цилиндра следует начинать с определения основных пропорциональных величин — диаметра оснований и высоты.
Построение плоскостей кругов оснований производят тем же способом, что и при изображении окружностей — вписыванием в квадрат (рис.48).
Ось вращения тела (ось цилиндра) всегда перпендикулярна к плоскостям кругов основания. При прорисовывании окружности в квадратах их вертикальные и горизонтальные оси попадают своими концами в середины сторон квадрата, т.е. в точки касания окружности со сторонами поверхности цилиндра (рис.48,49).
Рассматривая форму каркаса цилиндра, видим, что нижнее основание шире верхнего, следовательно, ближняя высота поверхности цилиндра больше, чем дальняя. Их различия обусловлены перспективной закономерностью. При этом необходимо заметить, что чрезмерно широкое нижнее основание цилиндра не способствует правильному и убедительному построению рисунка цилиндра. Поэтому ширина нижнего эллипса относительно верхнего должна быть чуть больше, равно как при наблюдении цилиндра с дальней точки зрения, а не с ближней.
При изображении окружностей оснований эллипса на гипсовом цилиндре его нижнее основание следует прорисовывать насквозь, т.е. видимым, с последующим его удалением для продолжения работы с помощью светотеней. Это даст возможность проследить за различиями в размерах оснований.
Завершив перспективное построение окружностей оснований цилиндра, приступайте к прорисовке краев формы образующей поверхности, соединяющей оба круга. При этом линии не должны быть чрезмерно контрастными, так как они находятся дальше, чем ближние поверхности цилиндра — ближние края эллипса и его изображающая поверхность. Однако без усиления линий ближних краев оснований получить в рисунке достаточное впечатление объемно-пространственной формы невозможно.
Читайте также: Как воткнуть поршень в цилиндр
По окончании работы над построением рисунка цилиндра необходимо приступить к его проверке. Проверять следует, отходя от своего места на расстояние не менее 2-4 м, в зависимости от размера рисунка. Чем больше его размер, тем с большего расстояния его следует рассматривать.
Внимательно проверив допущенные в процессе работы ошибки, их следует, не откладывая, исправить.
Изображение цилиндра в горизонтальном положении имеет свои особенности в отличие от построения цилиндра в вертикальном положении. Это обусловлено его цилиндрической образующей поверхностью, связывающей между собой оба круглых основания цилиндра. Для примера рассмотрим каркас цилиндра (рис.52).
Цилиндр в горизонтальном положении можно строить на основе прямоугольной призмы. Это облегчает объемно-пространственное и конструктивное построение цилиндра, позволяет правильно определить ось вращения по отношению к оси эллипса и, следовательно, правильно строить окружности оснований (эллипсы). Определив линию горизонта и положение предмета в пространстве относительно угла зрения (в этом случае цилиндр находится несколько сбоку, а точка зрения выше цилиндра), нужно наметить его местоположение. При построении очень важно правильно определить углы горизонтальных направлений предмета на плоскости, поэтому изображение призмы начинают с построения ее основания, у которого все стороны попарно равны высоте цилиндра и диаметру оснований окружностей. В последующем эта призма будет служить каркасом для построения цилиндра в горизонтальном положении.
Построение призмы производят с ближайших к нам точек на пересечении сторон параллелепипеда. В соответствии с положением предмета нужно наметить горизонтальную, уходящую по направлению к точкам схода линию основания сторон призмы. Направления этих двух основных линий, идущих к точкам схода, должны определять основу для правильного построения призмы, а затем — цилиндра. После чего производят построение с учетом перспективы. Для определения точек осевой линии призмы следует провести диагонали противоположных углов ее передней грани. Точка пересечения диагоналей будет центром оси призмы и цилиндра. Чтобы правильно вписать окружность основания цилиндра (эллипс) в переднюю грань призмы, необходимо точно определить прямой угол между осью призмы и отрезком линии, которая и будет большой осью эллипса. Эта важная деталь, о ней следует всегда помнить студентам, является причиной грубых ошибок при изображении цилиндра в горизонтальном положении. При этом, независимо от ракурсов и углов поворота, прямой угол между большой осью эллипса и осью вращения тела является основой для правильного построения окружностей оснований в его горизонтальном положении.
Итак, определив прямой угол, приступайте к вписыванию окружностей оснований цилиндра. Здесь большая ось будет определять наибольший диаметр основания, а малая, которая располагается по оси цилиндра, — наименьший.
Следует обратить внимание, что дальнее основание цилиндра по мере удаления от рисующего всегда несколько шире (по малой оси), чем переднее. Это обусловлено закономерностью перспективы.
Построив таким образом основания и дополнительно уточнив окружности (эллипсы), соединяют их образующими. В завершающей стадии построения изображения следует придать рисунку большую пространственность за счет усиления линий близлежащих и ослабления линий дальних форм.
Завершив построение, следует непременно его проверить. Внимательно проверив возможные ошибки, допущенные в процессе построения, и исправив их (если таковые имеются), следует перейти к длительному рисунку с помощью света, тени, полутени и рефлекса.
Для продолжения работы над длительным рисунком студентам необходимо дополнительное изучение закономерностей распределения светотеней. Без этого невозможно переходить к практическому выполнению учебных задач в академическом учебном рисунке. Вопросы, касающиеся законов света и теней, изложены в конце этого раздела.
📸 Видео
Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Построение проекций точек пересечения наклонного цилиндра прямой линиейСкачать

Построение изометрии цилиндраСкачать

Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Начертательная геометрия. Пересечение прямых с поверхностями вращения. Задача 53гСкачать

Пересечение поверхностей полусферы и цилиндра. Пошаговое видео. Инженерная графикаСкачать

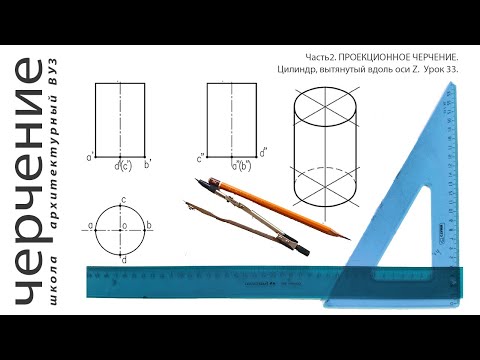
Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Построение проекций точек на поверхности конуса #черчение #проекции #конус #преподавательСкачать

РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Точка встречи прямой с поверхностью конусаСкачать

Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать










