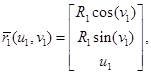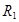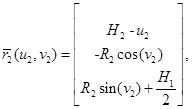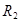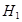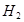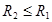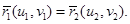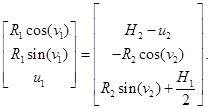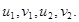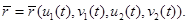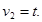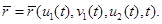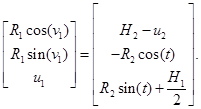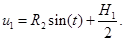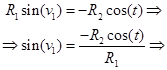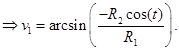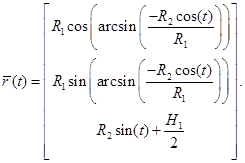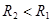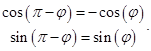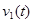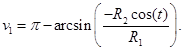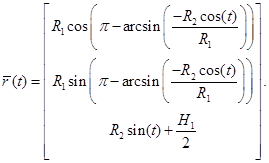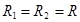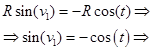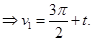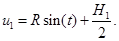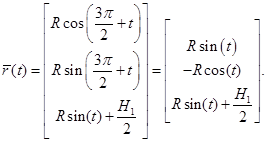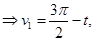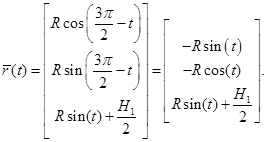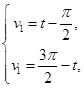Как найти точки пересечения цилиндра

Пересечение прямой с поверхностью цилиндра — это задача по определению точек встречи прямой с поверхностью цилиндра. Поверхность цилиндра представляет собой поверхность вращения с образующей в виде прямой линии.

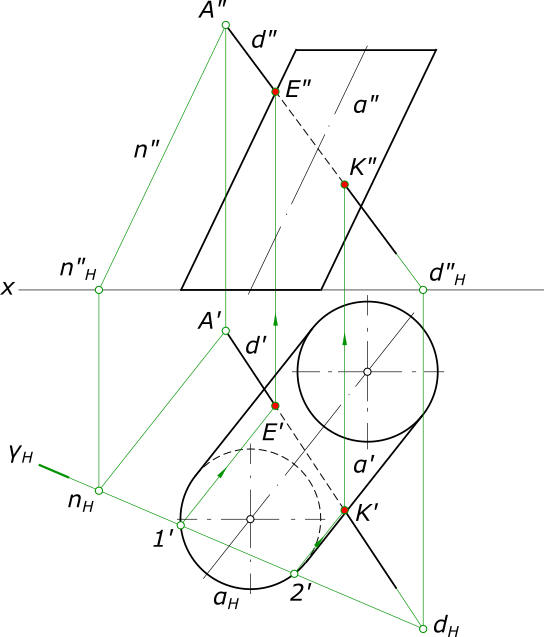
Пересечение прямой с поверхностью цилиндра: d ∩ α = ?

Здесь прямая d занимают общее положение и поверхность цилиндра α формируется прямыми из вершины S, находящейся в несобственной точке. Решать задачу на пересечение прямой с конусом следует, применяя алгоритм пересечения прямой с поверхностью: — Заключаем прямую d в вспомогательную плоскость γ, которая пересечет цилиндр по прямым линиям — образующим. Плоскость γ задаем пересечением прямой d и прямой n параллельной образующим цилиндра; — Находим точки пересечения 1 и 2 этой плоскости с основанием цилиндра, для чего строим горизонтальный след плоскости — γH по следам прямых nH и dH; — В пересечении образующих цилиндра 1 и 2 с прямой d находим искомые точки E и K пересечения прямой с поверхностью цилиндра.

Пересечение прямой с поверхностью цилиндра — это также задача по определению видимости с помощью конкурирующих точек: — для горизонтальной плоскости проекций. Образующие 1 и 2 видимы. Прямая d видима за пределами отрезка EK; — для фронтальной плоскости проекций. Образующие 1 и 2 видимы. Прямая d видима за пределами отрезка EK.

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Лекция 8. Пересечение кривых поверхностей

В общем случае кривые поверхности второго порядка (цилиндр, конус, сфера) пересекаются по пространственной кривой четвертого порядка. Эта лекальная кривая строится по точкам.

В общем случае эти точки находятся как точки пересечения образующих одной поверхности с образующими другой, а потом точки последовательно соединяют линией с учётом видимости.

Видео:Построение точек встречи прямой с поверхностью конусаСкачать

8.1. Частные случаи

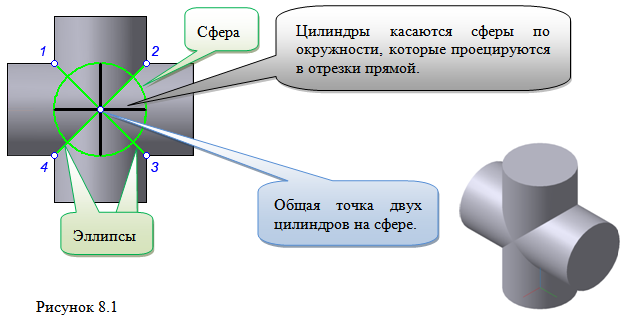
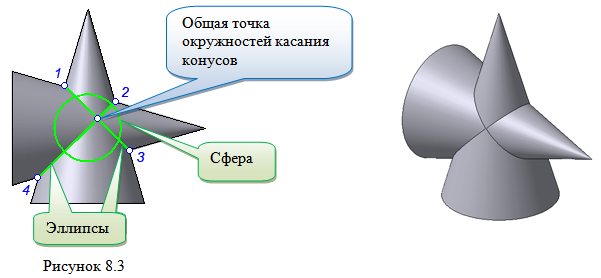
Теорема Монжа 1 . Две поверхности, описанные вокруг общей сферы, пересекаются по двум плоским кривым (Рисунок 8.1).

Крайние образующие цилиндров пересекаются в точках 1, 2, 3, 4.
Цилиндры пересекаются по эллипсам.

Крайние образующие пересекаются в точках 1, 2, 3, 4.

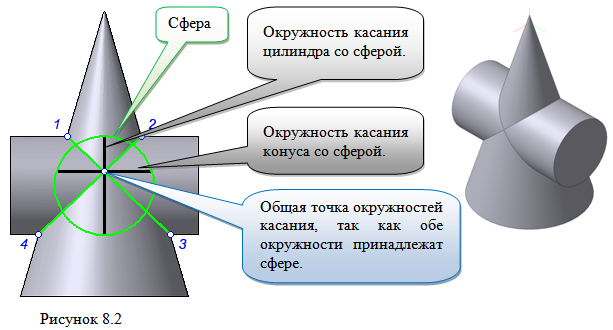
Теорема Монжа 2 . Если две пересекающиеся поверхности второго порядка имеют общую плоскость симметрии, параллельную некоторой плоскости проекций, то на эту плоскость проекций линия их пересечения проецируется в кривую второго порядка. Если это условие не выполнено, то – в кривую четвертого порядка. Эту плоскость называют плоскостью параллелизма .

Читайте также: Задний тормозной цилиндр ниссан примера р11

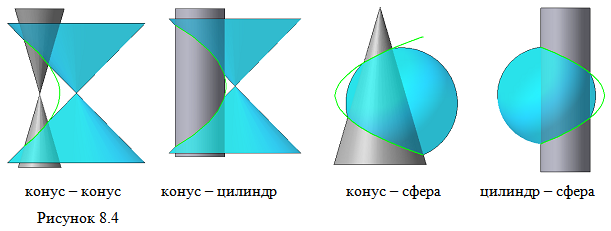
Рассмотрим четыре примера пересечения тел вращения, у которых оси вращения лежат в одной плоскости, параллельной плоскости проекций π₂ (Рисунок 8.4). Следовательно, данная плоскость является плоскостью симметрии пересекающихся тел, параллельная плоскости проекций π₂. Это означает, что линия пересечений тел проецируется на плоскость проекций π₂ как кривая второго порядка – парабола.

Видео:Построение проекций точек пересечения наклонного цилиндра прямой линиейСкачать

8.2. Алгоритм построения точек кривой пересечения двух поверхностей

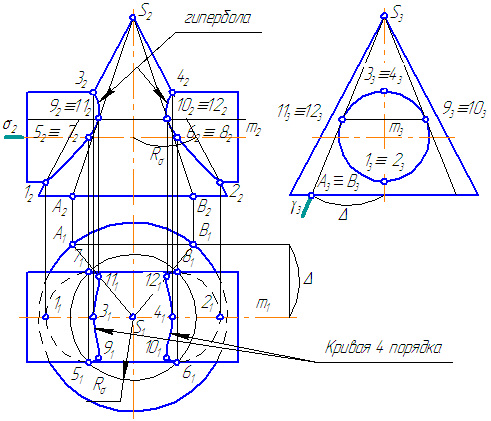
1. Выполним анализ кривых пересечения цилиндра и конуса (Рисунок 8.5): у данных тел есть общая плоскость симметрии, параллельная плоскости проекций π₂, следовательно, (согласно второй теореме Монжа) на π₂ кривые пересечения тел 4-го порядка проецируются в виде кривых второго порядка. Поскольку при этом получается две ветви, следовательно, это будет гипербола.
2. Строим характерные точки: пересечение крайних образующих на π₂ цилиндра и конуса, точки 1, 2, 3, 4.
3. Для нахождения точек, лежащих на крайних образующих на π1 цилиндра, введём плоскость σ⊥π2 и σ//π1 проходящую через фронтальную проекцию оси вращения цилиндра. В результате данная плоскость пересечет цилиндр по крайним образующим, а конус – по окружности радиусом Rσ. Построенные на π1 сечения пересекутся в точках 5, 6, 7, 8. По линии проекционной связи строим их фронтальные проекции.
4. Для построения самых близких друг к другу точек кривой на π2 введём плоскость γ⊥π3, проходящую через вершину конуса и касательную к цилиндру. Данная плоскость пересечёт конус по треугольнику SAB. Построив образующие конуса SA, SB и цилиндра 11-12, на их пересечении определим точки 11, 12. Точки 9, 10 построим симметрично точкам 11 и 12.
5. Для построения дополнительных промежуточных точек, можно ввести вспомогательные секущие плоскости (посредники) параллельно σ.

Рисунок 8.5 – Построение линии пересечения конуса и цилиндра

На анимации ниже представлена последовательность построения линии пересечения конуса и цилиндра.

Рисунок 8.6 – Последовательность построения линии пересечения конуса и цилиндра

Видео:ЦИЛИНДР. Проекции точек на его поверхности. Достроить недостающие проекции точек на трех плоскостяхСкачать

8.3. Задачи для самостоятельной работы

1-2. Построить линию пересечения поверхностей вращения (Рисунки 8.7, 8.8).

Видео:РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Построение линии пересечения двух цилиндров в параметрическом виде

Рубрика: 14. Общие вопросы технических наук

Статья просмотрена: 3136 раз

Библиографическое описание:

Князев, Д. Н. Построение линии пересечения двух цилиндров в параметрическом виде / Д. Н. Князев, Е. С. Устинова. — Текст : непосредственный // Технические науки в России и за рубежом : материалы IV Междунар. науч. конф. (г. Москва, январь 2015 г.). — Москва : Буки-Веди, 2015. — С. 122-125. — URL: https://moluch.ru/conf/tech/archive/124/7023/ (дата обращения: 29.10.2021).

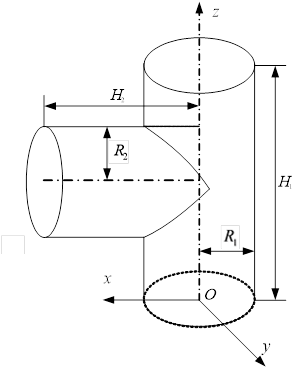
Для производства методом намотки из композиционных материалов элементов трансформируемых конструкций типа тройник, имеющего геометрическую форму двух пересекающихся цилиндров (рис. 1), необходимо иметь математическую модель такого объекта. Важным элементом такой модели является уравнение линии пересечения цилиндров.

Рис. 1. Линия пересечения двух цилиндров

Параметрическое уравнение первого цилиндра (рис. 1) имеет вид:

(1)

где — радиус первого цилиндра.

Параметрическое уравнение второго цилиндра (рис. 1) имеет вид:

где — радиус второго цилиндра,

— высота первого цилиндра,

— высота второго цилиндра.

Для заданной конфигурации цилиндров зададим дополнительное условие, ограничивающее радиус второго цилиндра:.

Читайте также: Суппорт тормозного цилиндра для лачетти

Условие пересечения цилиндров выглядит следующим образом:

(2)

Последняя система уравнений содержит три уравнения и четыре неизвестных величины:

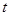
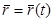
Введем для линии пересечения параметр , то есть — линия пересечения двух цилиндров.

(3)

Примем, что Тогда (3) запишется следующим образом:

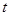
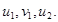
Теперь, так как параметр является задаваемой величиной, система (2) зависит от трех переменных: C учетом этого перепишем систему (2) следующим образом:

(4)

Из третьего уравнения системы (4) имеем:

(5)

Из второго уравнения системы (4) имеем:

(6)

Подставив (5) и (6) в систему (1), получим систему уравнений для линии пересечения цилиндров:

(7)

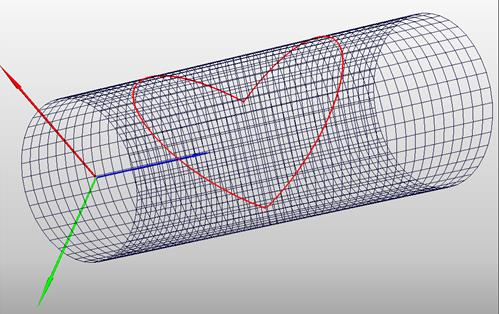
Линия пересечения при значении радиусов цилиндров представлена на рисунке 2.

Рис. 2. Линия пересечения цилиндров разного радиуса

Первое уравнение системы (7) дает положительные значения координаты X, что позволяем нам задать уравнения линии пересечения в положительном направлении оси X. Для получения уравнения линии пересечения в отрицательном направлении оси X необходимо получить отрицательные значения первого уравнения системы (7).

Воспользуемся тригонометрическими формулами приведения:

Параметр принимает следующий вид:

Уравнение для второй линий пересечения принимает вид:

Изображение второй линии пересечения представлено на рисунке 3.

Рис. 3. Вторая линия пересечения

Рассмотрим частный случай, в котором значения радиусов цилиндров равны . Из второго уравнения системы (4), на основании известных тригонометрических формул приведения, получим:

(8)

Из третьего уравнения системы (4) имеем:

(9)

Подставив (8) и (9) в систему (1), получим уравнение линии пересечения цилиндров (уравнение первого эллипса) равного радиуса:

(10)

Выражение для :

(11)

также является верным, так как с его помощью можно выразить уравнение второго эллипса, по которому пересекаются цилиндры, подставив (9) и (11) в систему (1). Уравнение второй линии пересечения имеет вид:

(12)

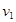
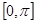
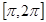
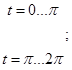
Системы уравнений (10) и (12) определяют эллипсы пересечения цилиндров. Для удобства рассмотрения выделим линии пересечения в положительном и отрицательном направлении оси Х через переопределение на интервалах и :

(13)

Используя для определения систему (13), можно получить линию пересечения цилиндров равного радиуса в положительном направлении оси Х, а используя систему (14) — в отрицательном.

Линия пересечения цилиндров равного радиуса в положительном направлении оси Х представлена на рисунке 4.

Рис. 4. Линия пересечения цилиндров равного радиуса

Видео:Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

Похожие статьи

Способ создания линии пересечения поверхностей вращения

Построение линии пересечения двух цилиндров. Уравнение для второй линий пересечения принимает вид: Изображение второй линии пересечения представлено на рисунке 3. Линия пересечения цилиндров равного радиуса в положительном.

Линия пересечения цилиндров равного радиуса.

Рис. 1. Линия пересечения двух цилиндров. Параметрическое уравнение первого цилиндра (рис. 1) имеет вид: (1). Линия пересечения цилиндров равного радиуса в положительном направлении оси Х представлена на рисунке 4.

Исследование свойств поверхностей вращения с использованием.

Поверхность, задаваемая уравнением , называется двуполостным гиперболоидом. Если поверхность пересечь плоскостями z=h, то линия пересечения определяется системой уравнений

Касательная. Задачи на касательную | Статья в журнале.

Составим уравнение касательной к графику заданной функции в точке : Так как эта прямая проходит через точку (2;3), то имеет место равенство , откуда находим: . Может ли касательная к кривой в какой-либо ее точке составлять острый угол с положительным направлением оси ?

Читайте также: Цилиндры с ключами evva

Об определении некоторых геометрических параметров.

После решения системы уравнений (9) получим уравнение прямой D1D3

С целью определения точек пересечения линии наибольшего наклона плоскости S к горизонту, проходящую через т. D1, с периметром площади АВС, определим точки пересечения.

Математическое моделирование взаимодействия ионов.

Расположим дипольные частицы в плоскости цилиндра диаметром равном , ось цилиндра параллельна оси .

Проведём окружность с центром в точке Q и радиусом 2 см, находим точку пересечения

Тогда динамику движения частиц можно описать уравнениями системы (1–3).

Сечение поверхностей 2-го порядка общего вида по эллипсу.

Способ создания линии пересечения поверхностей вращения. Создание горизонтальной проекции линии пересечения по фронтальной проекции не является сложным.

Расчёт фундаментных плит методом конечных элементов

Построение линии пересечения двух цилиндров. Важным элементом такой модели является уравнение линии пересечения цилиндров. Из второго уравнения системы (4), на основании известных тригонометрических формул приведения.

Евклидова плоскость в четырехмерном пространстве

Построение линии пересечения двух цилиндров в параметрическом виде. Анализ и разработка измерительной установки для определения момента инерции тел вращения сложной формы.

Видео:Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

Похожие статьи

Способ создания линии пересечения поверхностей вращения

Построение линии пересечения двух цилиндров. Уравнение для второй линий пересечения принимает вид: Изображение второй линии пересечения представлено на рисунке 3. Линия пересечения цилиндров равного радиуса в положительном.

Линия пересечения цилиндров равного радиуса.

Рис. 1. Линия пересечения двух цилиндров. Параметрическое уравнение первого цилиндра (рис. 1) имеет вид: (1). Линия пересечения цилиндров равного радиуса в положительном направлении оси Х представлена на рисунке 4.

Исследование свойств поверхностей вращения с использованием.

Поверхность, задаваемая уравнением , называется двуполостным гиперболоидом. Если поверхность пересечь плоскостями z=h, то линия пересечения определяется системой уравнений

Касательная. Задачи на касательную | Статья в журнале.

Составим уравнение касательной к графику заданной функции в точке : Так как эта прямая проходит через точку (2;3), то имеет место равенство , откуда находим: . Может ли касательная к кривой в какой-либо ее точке составлять острый угол с положительным направлением оси ?

Об определении некоторых геометрических параметров.

После решения системы уравнений (9) получим уравнение прямой D1D3

С целью определения точек пересечения линии наибольшего наклона плоскости S к горизонту, проходящую через т. D1, с периметром площади АВС, определим точки пересечения.

Математическое моделирование взаимодействия ионов.

Расположим дипольные частицы в плоскости цилиндра диаметром равном , ось цилиндра параллельна оси .

Проведём окружность с центром в точке Q и радиусом 2 см, находим точку пересечения

Тогда динамику движения частиц можно описать уравнениями системы (1–3).

Сечение поверхностей 2-го порядка общего вида по эллипсу.

Способ создания линии пересечения поверхностей вращения. Создание горизонтальной проекции линии пересечения по фронтальной проекции не является сложным.

Расчёт фундаментных плит методом конечных элементов

Построение линии пересечения двух цилиндров. Важным элементом такой модели является уравнение линии пересечения цилиндров. Из второго уравнения системы (4), на основании известных тригонометрических формул приведения.

Евклидова плоскость в четырехмерном пространстве

Построение линии пересечения двух цилиндров в параметрическом виде. Анализ и разработка измерительной установки для определения момента инерции тел вращения сложной формы.

💡 Видео

Точка встречи прямой с поверхностью конусаСкачать

Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Начертательная геометрия. Пересечение прямых с поверхностями вращения. Задача 53гСкачать

Пересечение поверхностей полусферы и цилиндра. Пошаговое видео. Инженерная графикаСкачать

Задание 50. Построение ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ЦИЛИНДРОВСкачать

Точки пересечения прямой с поверхностью/Points of intersection of a straight line with a surface.Скачать

2 3 проекция точки на конусеСкачать

Построение точек встречи прямой m с поверхностью сферыСкачать

Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ КОНУСА. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯСкачать

36. Построение развертки цилиндра с линией пересеченияСкачать

85КБ. Пересечение поверхностей цилиндра и полусферы. Определение видимости.Скачать