Как найти центр масс составного цилиндра (7 видео)

Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.

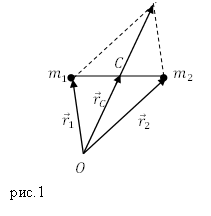
Если разбить тело на элементарные части объемом ∆V_i , то на каждую его часть будет действовать сила притяжения ∆P_i, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.

Рис.1. Параллельная система сил

Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.

При определении центра тяжести полезны несколько теорем.

1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой

2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.

§2. Способы определения координат центра тяжести.

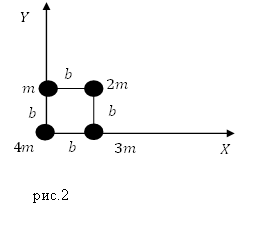
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

Рис.2. Центр тяжести тел, имеющих ось симметрии

2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.

Рис.3. Центр тяжести сплошной

сложной геометрической фигуры

— центр тяжести и площадь первой фигуры;

— центр тяжести и площадь второй фигуры;

— координата центра тяжести сплошной сложной геометрической фигуры по оси x;

— координата центра тяжести сплошной сложной геометрической фигуры по оси y;

3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S₁ и площади вырезанной части S₂ .

Рис.4. Центр тяжести сложной геометрической фигуры,

— центр тяжести и площадь первой фигуры;

— центр тяжести и площадь второй фигуры;

— координата центра тяжести сложной геометрической фигуры по оси x;

— координата центра тяжести сложной геометрической фигуры по оси y;

§3. Координаты центра тяжести некоторых простых фигур.

1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: x_c =1/3(x₁+x₂+x₃) ; y_c =1/3(y₁+y₂+y₃).

Рис.5. Центр тяжести треугольника

2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: x_c =b/2 ; y_c =h/2.

Читайте также: Открытый участок мембраны осевого цилиндра в котором миелиновая оболочка прерывается

Рис. 6. Центр тяжести треугольника

3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: x_c =D/2 ; y_c =4R/3π.

Рис. 7. Центр тяжести полукруга

4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: x_c =R ; y_c =R.

Рис. 8. Центр тяжести круга

Вопросы для самопроверки:

— Что называется центром параллельных сил?

— Что называется центром тяжести тела?

— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?

— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?

— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?

— Как используются свойства симметрии при определении центров тяжести тел?

— В чем состоит сущность способа отрицательных площадей?

— Каким графическим построением можно найти центр тяжести треугольника?

— Запишите формулу, определяющую центр тяжести треугольника.

Содержание

Определение центра масс
Радиус-вектор и координаты центра масс
Скорость центра масс
Примеры задач на определение центра масс
3.5. Центр масс
📽️ Видео

Видео:Определение центра тяжести сложных сечений. Фигуры из ГОСТ.Скачать

Определение центра масс

При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.

Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.

Видео:Центр тяжести фигуры неправильной формы.Скачать

Радиус-вектор и координаты центра масс

Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: $ >_1\ и\ >_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором $ >_C$ (рис.1).

Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен $ >_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:

Радиус -вектор $ >_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц $ >_1$ и $ >_2$. Это становится очевидным, если формулу (2) представить в виде:

Выражение (3) показывает, что радиус-вектор каждой частицы входит в $ >_C$ с весом, который пропорционален его массе.

Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.

Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:

Выражение (4) считают определением центра масс системы.

При этом абсцисса центра масс равна:

Ордината ($y_c$) центра масс и его аппликата ($z_c$):

Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.

Читайте также: Сколько сантиметров в одном цилиндре

Видео:Центр тяжести. ЭкспериментСкачать

Скорость центра масс

Выражение для скорости центра масс ($ >_c=\frac >_c>

$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.

Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.

Видео:Определение центра тяжести сложной фигуры. СопроматСкачать

Примеры задач на определение центра масс

Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?

Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:

Вычислим массу рассматриваемой системы точек:

Тогда абсцисса центра масс $x_ \ $равна:

Ответ. $x_c=0,5\ b$; $y_с=0,3\ b$

Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.

Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.

В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:

Видео:Видеоурок 3. Определение центра тяжести.Скачать

3.5. Центр масс

Снова рассмотрим ту же систему материальных точек. Построим радиус-вектор по следующему правилу:

где — радиус-вектор — той материальной точки системы, а — ее масса.

Радиус-вектор определяет положение в пространстве центра инерции (центра масс) системы.

Вовсе не обязательно, что в центре масс системы окажется какая-то материальная точка.

Пример. Найдем центр масс системы, состоящей из двух маленьких шариков — материальных точек, соединенных невесомым стержнем (рис. 3.29). Такая система тел называется гантелей.

Рис. 3.29. Центр масс гантели

Подставляя в эти равенства выражение для радиус-вектора центра масс

Отсюда следует, что центр масс лежит на прямой, проходящей через центры шаров. Расстояния l₁ и l₂ между шарами и центром масс равны соответственно

Центр масс ближе к тому шарику, масса которого больше, что видно из отношения:

Определим, с какой скоростью движется центр инерции системы. Дифференцируем по времени обе части:

Читайте также: Диаметр цилиндра двигателя газ 3307

В числителе полученного выражения в правой части стоит сумма импульсов всех точек, то есть импульс системы. В знаменателе стоит полная масса системы

Мы получили, что скорость центра инерции связана с импульсом системы и ее полной массой таким же соотношением, какое справедливо для материальной точки:

Видео 3.11. Движение центра масс двух одинаковых тележек, связанных пружиной.

Таким образом, можно считать, что скорость V_C является скоростью системы как целого. Она, разумеется, может отличаться от скоростей каждого из тел, входящих в систему.

Центр масс замкнутой системы движется всегда с постоянной скоростью, поскольку импульс такой системы сохраняется.

Если продифференцировать теперь выражение для импульса системы по времени и учесть, что производная импульса системы есть равнодействующая внешних сил, то получим уравнение движения центра масс системы в общем случае:

Центр масс системы движется точно так же, как двигалась бы материальная точка с массой, равной массе всех частиц системы, под действием векторной суммы всех внешних сил, приложенных к системе.

Если имеется система материальных точек, внутреннее расположение и движение которых нас не интересует, мы вправе считать ее материальной точкой с координатами радиус-вектора центра инерции и массой, равной сумме масс материальных точек системы.

Если связать с центром масс замкнутой системы материальных точек (частиц) систему отсчета (ее называют системой центра масс), то полный импульс всех частиц в такой системе окажется равным нулю. Таким образом, в системе центра масс замкнутая система частиц как целое покоится, и существует только движение частиц относительно центра масс. Поэтому ясно выявляются свойства внутренних процессов, протекающих в замкнутой системе.

В случае, когда системой является тело с непрерывным распределением масс, определение центра масс остается по существу тем же. Окружаем произвольную точку в нашем теле небольшим объемом . Масса, заключенная в этом объеме, равна , где — плотность вещества тела, которая может и не быть постоянной по его объему. Сумма по всем таким элементарным массам заменяется теперь на интеграл по всему объему тела, так что для положения центра масс тела получается выражение

Если вещество тела однородно, плотность его постоянна, и ее можно вынести из-под знака интеграла, так что она сократится в числителе и знаменателе. Тогда выражение для радиус-вектора центра масс тела принимает вид

где — объем тела.

И в случае непрерывного распределения масс справедливо утверждение, что

Центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием векторной суммы всех внешних сил,приложенных к телу.

Пример. Если снаряд взрывается в некоторой точке своей параболической траектории, то осколки летят по самым различным траекториям, но его центр масс продолжает движение по параболе.