Как называется фигура четверть цилиндра (7 видео)

Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.

Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.

Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.

Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.

Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.

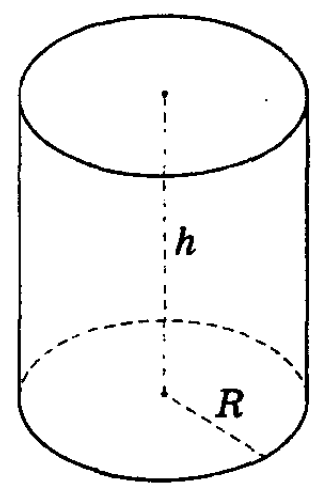
Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.

Круговой цилиндр — цилиндр, основания которого являются кругами.

Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.

Радиус цилиндра – радиус его основания.

Образующая цилиндра — образующая цилиндрической поверхности.

Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.

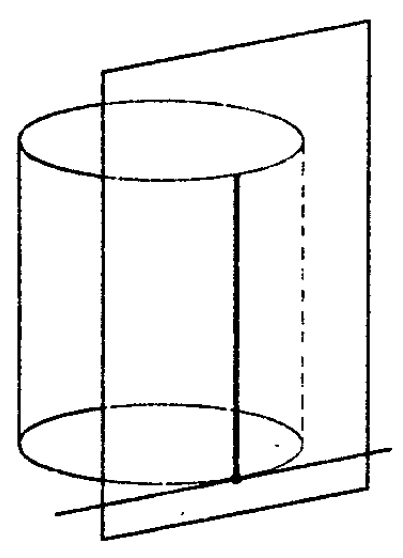
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.

Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.

Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_ =2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.

Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_ =2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.

Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).

Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.

Содержание

Как называется фигура четверть цилиндра
Геометрические тела. Цилиндр.
Формулы нахождения элементов цилиндра.
Что такое цилиндр: определение, элементы, виды, варианты сечения
Определение цилиндра
Основные элементы цилиндра
Знакомство с геометрическим телом — Цилиндром.
📽️ Видео

Видео:Объемные Геометрические ФИГУРЫ Загадки для ДЕТЕЙСкачать

Как называется фигура четверть цилиндра

Ц илиндр, получается в результате вращения прямоугольника вокруг одной из его сторон.

Цилиндр состоит из двух кругов и множества отрезков .
Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов.
Определения элементов цилиндра :

Основания цилиндра – равные круги, расположенные в параллельных плоскостях

Читайте также: Задиры в цилиндрах ниссан икстрейл

Высота цилиндра — это расстояние между плоскостями его оснований.

Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра).

Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники

Образующая цилиндра — это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра.

Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра .

Радиус цилиндра – это радиус его основания.

Прямой цилиндр – это цилиндр, образующие которого перпендикулярны основанию.

Равновеликий цилиндр – цилиндр, у которого высота равна диаметру (показать равновеликий цилиндр: кнопкой со значком руки перевести модель обратно в интерактивный режим и изменить значение высоты и радиуса у предложенной модели так, чтобы ).

Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C , где H – высота цилиндра, а C – длина окружности основания. Получим формулы для вычисления площадей боковой S _б и полной S _п поверхностей: S _б = H · C = 2π RH , S _п = S _б + 2 S = 2π R ( R + H ).

Задача № 1. Вычислить площадь боковой и полной поверхности цилиндра, у которого радиус равен 3 см, а высота 5 см (число пи и ответ округлить до целых).

2. Высота цилиндра равна h , радиус основания R . Найти площадь сечения плоскостью, проведенной параллельно оси цилиндра на, расстоянии a от нее.

Домашнее задание: 522, 524, 526.

Р.S/ кому интересно попрбуйте пройти по ссылке и посмотреть электронный ресурс про цилиндр

для начала на странице установите у себя на ПК модуль ОМS и закачайте модуль. На выскочившей таблице кликните воспроизвести. А дальше по порядку просмотрите все странички.
ВСЕМ СПАСИБО.

Видео:Объём цилиндраСкачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:Объёмные геометрические фигуры. Куб. Цилиндр. Конус. Шар // Математика 1 классСкачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:Построение врезок двух геометрических фигурСкачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:Цилиндр, конус, шар, 6 классСкачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Основные элементы цилиндра

Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Знакомство с геометрическим телом — Цилиндром.

Екатерина Искаева
Знакомство с геометрическим телом — Цилиндром.

Задачи: 1. Формировать представление о цилиндре, умение распознавать цилиндр в предметах окружающей обстановки.

2. Закреплять счет в пределах 5, геометрические представления детей, умение находить общие свойства предметов.

Материал: картинки с изображением предметов цилиндрической формы, цилиндры разного диаметра и высоты, карточки с «паспортом» цилиндра, модели цилиндров и кубик, цифры 1 – 5, набор геометрических фигур на каждого ребенка.

1. Знакомство с цилиндром и его свойствами.

Воспитатель показывает картинки предметов цилиндрической формы: стакан, колбасу, шляпу-цилиндр, банку цилиндрической формы, клеящий карандаш.

— Что общего у всех этих предметов вы заметили? (У всех предметов похожа форма.)

Если дети затрудняются ответить на этот вопрос, можно задать наводящие вопросы: одинаков ли материал, из которого сделаны эти предметы, их цвет, размер, назначение.

Затем воспитатель сообщает детям, что предметы такой формы называются цилиндрами, и просит их найти цилиндры на своем столе. Вместе с цилиндрами на столе должны быть предметы и других форм (например, шара, параллелепипеда, конуса). Целесообразно показать также картинки, на которых предметы цилиндрической формы являются элементами: пушка, здание с колоннами, дерево и т. д.

Далее дети знакомятся со свойствами цилиндра.

— Знаете ли вы, почему цилиндр так называется? Очень давно, когда никаких машин еще не было, люди передвигали тяжелые предметы при помощи стволов деревьев. Подумайте – как?

Воспитатель дает детям несколько цилиндров одинакового диаметра (например, карандаши) и кубик и предлагает представить, что кубик – это очень тяжелый груз, который надо переместить с одного конца стола на другой, используя цилиндры. После выполнения задачи воспитатель рассказывает, что слово «цилиндр» в переводе с греческого – «каток», «валик». Одним из его свойств является то, что его можно катить.

Детям предлагается разойтись по группе и найти предметы цилиндрической формы.

Затем дети возвращаются к столу, на котором стоят разные цилиндры. Им предлагается найти фигуры, одинаковые по какому-либо признаку, и у отобранных фигур найти признаки отличия. Например, это могут быть цилиндры, равные по высоте, но разные по толщине, цвету, материалу, из которого они сделаны (цилиндры можно сделать из бумаги, пластилина, взять пластмассовые, металлические цилиндры, деревянные карандаши и т. д.)

2. Физкультминутка: «Кто самый внимательный?»

По команде «Ухо» дети должны схватиться за ухо (можно усложнить, говоря «Правое ухо», по команде «Нос» — за нос. Воспитатель выполняет задание вместе с детьми. Через некоторое время начинает намеренно ошибаться и сбивать детей.

3. Игра: «Паспортный стол».

У детей на столах карточки от 1 до 5. Воспитатель предлагает им рассмотреть фигуры, сделанные из пластилина различных цветов.

Дети отвечают на вопросы воспитателя:

— Сколько всего фигур? (Показывают цифру.)

— Посчитайте от 1 до 5 и от 5 до 1.

— Сколько цилиндров? (Хлопают в ладоши.)

— Почему хлопнули 4 раза? (Вторая фигура – не цилиндр.)

— Чем вторая фигура отличается от остальных?

После всех рассуждений дети приходят к выводу, что у цилиндра с двух сторон одинаковые круги, а у второй фигуры – нет.

Воспитатель ставит цилиндр на стол и просит детей присесть так, чтобы фигура была на уровне глаз. Спрашивает детей о том. что они видят, как это можно зарисовать. Затем поворачивает цилиндр несколько раз и спрашивает детей о том же. В результате обсуждения приходят к выводу:

— Значит, если хотят рассказать о цилиндре, это делают так:

Это «паспорт» фигуры. О чем по нему можно узнать? (О высоте цилиндра, его толщине).

Воспитатель прикладывает цилиндр к прямоугольнику, а основания цилиндра – к кругам и показывает, как «паспорт» сопоставляется с его обладателем.

На столе у детей разные цилиндры. Каждому ребенку дается «паспорт», по которому он должен найти соответствующий этому «паспорту» цилиндр.

4. Игра: «Числовое лото».

Дети раскладывают на столе карточки с цифрами от 1 до 5 (лицом вниз). Карточки перемешиваются. Затем каждый ребенок должен вытащить наугад какую-нибудь карточку и выложить столько фигур «Геометрического лото», имеющих общий признак, сколько указывает цифра на карточке (например, 3 большие фигуры, или 4 красные фигуры, или 2 круга и т. д.).

После выполнения задания дети с воспитателем ходят по группе и проверяют правильность решения.

Требования к уровню подготовки воспитанников по дисциплине «Математика» во второй младшей группе. Количество и счёт: Счёт наизусть в пределах пяти, сравнивать группы предметов, содержащие до 5 предметов, сравнивать количество предметов,.