Как называется разрезанный цилиндр

Видео:Видеоурок по математике "Цилиндр"Скачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:Объём цилиндраСкачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

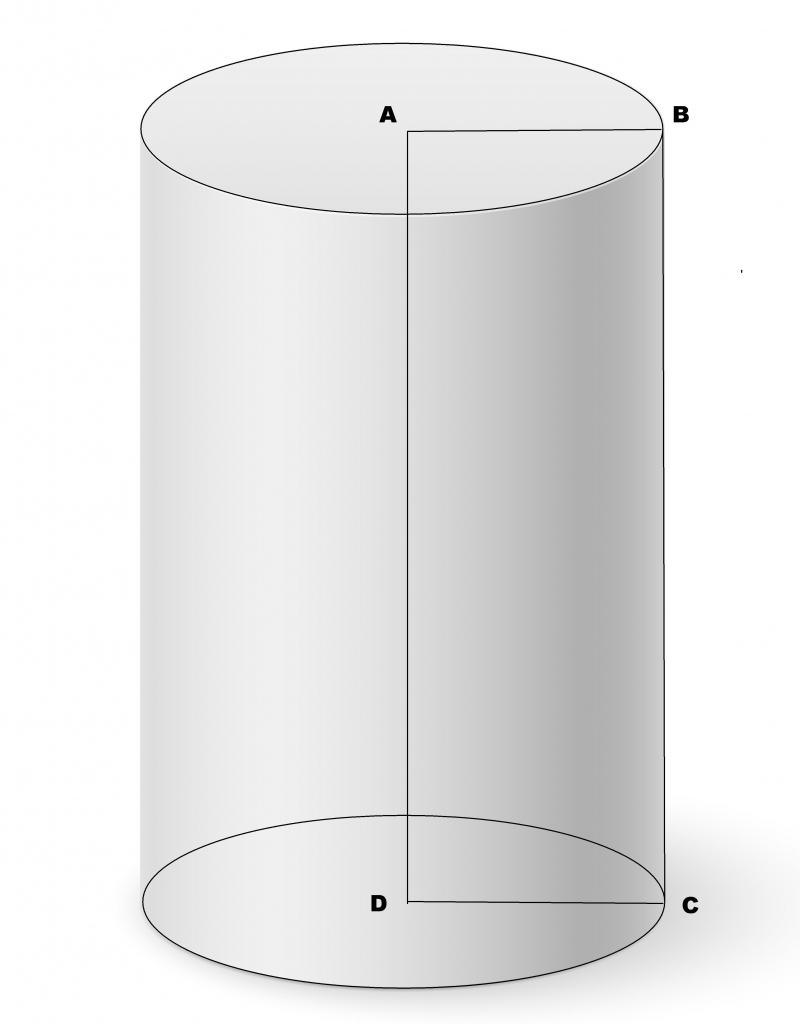
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Основные элементы цилиндра

• Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
• R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
• O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
• l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

• длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
• ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:Микрометр и нутромер. Как измерить цилиндры?Скачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:ЦилиндрСкачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:КАК ИЗМЕРИТЬ ЦИЛИНДРЫ? Учимся пользоваться нутромером и микрометромСкачать

Презентация по геометрии на тему «Цилиндр и его элементы»(11 класс)

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа № 45 Методическое пособие для учащихся 11 классов Составил учитель математики высшей категории Гавинская Елена Вячеславовна. г.Калининград 2016-2017 учебный год

В древности при строительстве грандиозных храмов и дворцов людям приходилось таскать и носить на себе огромные валуны и колонны. Тогда и было замечено, что катать предметы намного легче и удобнее. Примерно так и появились и популяризовались цилиндры. И по сей день эти тела вращения часто встречаются в нашей жизни. В архитектуре, в технике, в мире моды – цилиндры побывали везде.

Определение. Цилиндр (греч. kýlindros, валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).

Другие определения цилиндра. Цилиндр — это фигура, состоящая из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Цилиндром называется тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими эту поверхность. У Евклида цилиндр получается вращением прямоугольника. У Кавальери – движением образующей (при произвольной направляющей – «цилиндрика»).

Вклад Евклида в математику. О Евклиде почти ничего неизвестно, откуда он был родом, где и у кого учился. Папп Александрийский (III в.) сообщает, что он был очень доброжелателен ко всем тем, кто сделал хоть какой-нибудь вклад в математику, корректен, в высшей степени порядочен и совершенно лишен тщеславия. Евклид, как и другие великие греческие геометры, занимался астрономией, оптикой и теорией музыки. До нас дошли его сочинения, посвященные прикладным вопросам: «Феномены» (элементарная сферическая астрономия), «Оптика» (учение о перспективе) и «Сечение канона» ( теория музыки). Это были первые прообразы будущих исследований по математической физике: в них теория выводилась строго дедуктивно из явно сформулированных физических гипотез и математических постулатов. Гораздо больше мы знаем о математическом творчестве Евклида. Прежде всего Евклид является для нас автором «Начал», по которым учились математики всего мира. Эта удивительная книга пережила более двух тысячелетии, но до сих пор не утратила своего значения не только в истории науки, но и самой математике. Созданная там система евклидовой геометрии и теперь изучается во всех школах мира и лежит в основе почти всей практической деятельности людей. На геометрии Евклида базируется классическая механика, ее апофеозом было появление в 1687 г. Математических начал натуральной философии Ньютона, где законы земной и небесной механики и физики устанавливаются в абсолютном евклидовом пространстве. Содержание «Начал» далеко не исчерпывается элементарной геометрией — это основы всей античной математики. Здесь подводится итог более чем 300-летнему ее развитию и вместе с тем создается прочная 6aзa для дальнейших исследований. Последующие математики ссылались на предложения «Начал», как на нечто окончательно установленное.

Вклад Кавальери в математику. В своем основном труде «Геометрия» (1635г.) Кавальери развил разработанный им задолго до выхода книги новый метод определения площадей и объемов – так называемый метод неделимых. Неделимыми Кавальери называл параллельные между собой хорды плоской фигуры или параллельные плоскости тела. Важнейший признак неделимости состоит в том, что число измерений его на единицу меньше самого геометрического образа. У плоской фигуры 2 измерения, у ее неделимого, т.е. у отрезка – 1 измерение. Кавальери доказал теорему о том, что площади двух подобных фигур относятся как квадраты, а объемы – как кубы соответствующих неделимых, и установил, что отношение суммы квадратов всех неделимых треугольника к сумме квадратов всех неделимых параллелограмма, имеющего с треугольником одинаковые основания и высоту, равно 1:3. Впоследствии Кавальери нашел аналогичные соотношения для суммы кубов и т.д. до девятой степени неделимых. Труды Кавальери сыграли огромную роль в формировании исчисления бесконечно малых.

Элементы цилиндра. Круги, ограничивающие цилиндрическую поверхность называются основаниями цилиндра. Отрезки образующих, заключенные между основаниями, называются образующими цилиндра, а образованная ими поверхность – боковой поверхностью цилиндра. Ось цилиндрической поверхности называется осью цилиндра.

Свойства цилиндра. Основания равны и параллельны. Образующие равны и параллельны. Все сечения цилиндра плоскостями, параллельными плоскостям оснований цилиндра, равны основаниям цилиндра.

1. Основания циилиндра равны и параллельны. Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β, получается из окружности L параллельным переносом на вектор ОО1. Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор ОО1 окружность L перейдет в равную ей окружность L1 радиуса r с центром в точке О1. Доказательства свойств. α β L L1 о о1

2. Образующие цилиндра равны и параллельны. Все образующие цилиндра перпендикулярны к плоскостям оснований. Но плоскости оснований цилиндра параллельны. Значит, все образующие цилиндра – расстояния между параллельными плоскостями, следовательно, (по теореме) они равны и параллельны.

3. Все сечения цилиндра плоскостями, параллельными плоскостям оснований цилиндра, равны основаниям цилиндра. Действительно, любое такое сечение является общим основанием двух цилиндров, на которые секущая плоскость разбивает данный цилиндр. Поэтому оно равно другим основаниям этих цилиндров, которые являются основаниями исходного цилиндра.

Влияние оснований на цилиндр. Если основания цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости цилиндра перпендикулярны образующей, то цилиндр называется прямым. В частности, если основание стоящего на плоскости цилиндра — круг, то говорят о круговом (круглом) цилиндре; если эллипс — то эллиптическом. α β

Виды цилиндра. Бесконечное тело, ограниченное замкнутой бесконечной цилиндрической поверхностью, называется бесконечным цилиндром. Прямой круговой цилиндр — это поверхность, образованная вращением одной из параллельных прямых вокруг другой, принятой в качестве оси вращения. Бесконечное тело, ограниченное замкнутым цилиндрическим лучом и его основанием, называется открытым цилиндром. Основание и образующие цилиндрического луча называют соответственно основанием и образующими открытого цилиндра. Конечное тело, ограниченное замкнутой конечной цилиндрической поверхностью и двумя выделившими её сечениями, называется конечным цилиндром, или собственно цилиндром. Сечения называются основаниями цилиндра. По определению конечной цилиндрической поверхности, основания цилиндра равны.

Видео:Как Расточить Блок Цилиндров Своими РукамиСкачать

Круглый прямой цилиндр, развертка и формула для ее площади

Цилиндр — это одна из пространственных фигур, которая является объектом изучения стереометрии. Важная характеристика любой фигуры — это площадь ее поверхности. В данной статье рассмотрим, что собой представляет развертка цилиндра, а также покажем, как вычислить ее площадь.

Видео:9 класс, 41 урок, ЦилиндрСкачать

Цилиндр как фигура геометрии

Предположим, что у нас имеется некоторая плавная кривая. Это может быть круг, эллипс, парабола и так далее. Возьмем отрезок произвольной длины, который не лежит в плоскости кривой, и опишем с помощью него поверхность, следуя направлению кривой и транслируя отрезок параллельно самому себе. Полученная поверхность называется цилиндрической или просто цилиндром. Отмеченная кривая называется директрисой (направляющей), а отрезок — генератрисой (образующей).

Если к цилиндрической поверхности добавить еще две плоские одинаковые фигуры, ограничивающие эту поверхность с торцов, то полученное тело также называется цилиндром. Оно состоит из двух равных оснований и цилиндрической поверхности.

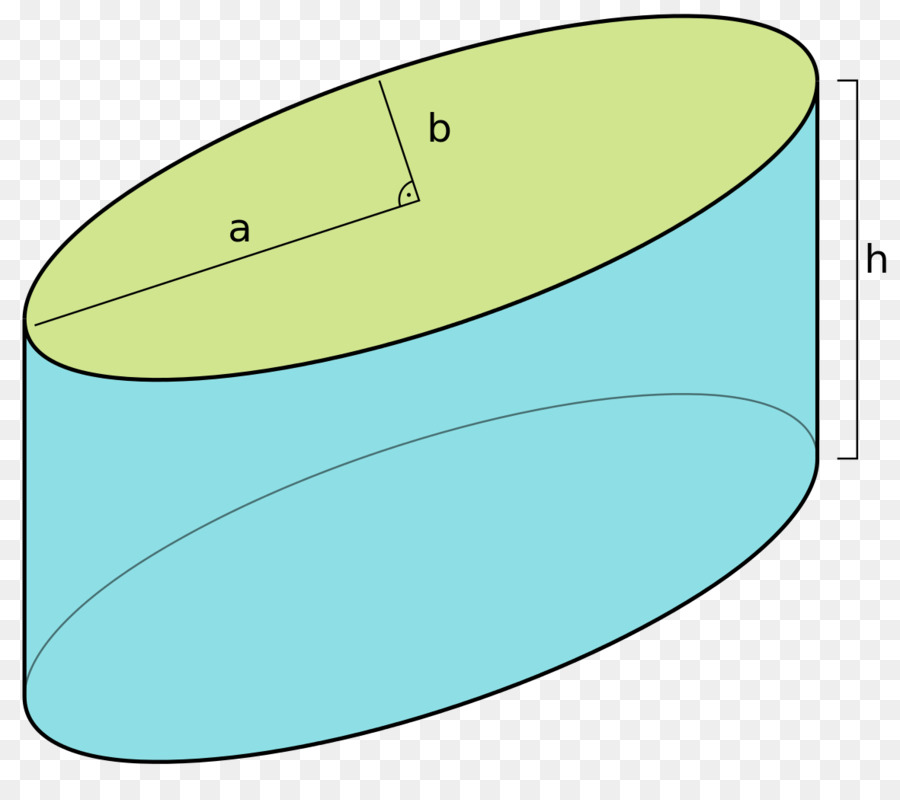
Для наглядного представления описанной фигуры ниже приведен рисунок. На нем изображен эллиптический цилиндр, имеющий полуоси a и b и высоту h (дистанция между основаниями).

Видео:Безумный способ открыть любой замок без ключа!Удивительный трюк со спичками,который отлично работаетСкачать

Круглый прямой цилиндр

Пусть директрисой будет окружность некоторого радиуса. Тогда образованная генератрисой фигура будет называться круглым цилиндром. Тем не менее генератриса относительно плоскости, ограниченной директрисой, может быть направлена произвольным образом. Поэтому в общем случае говорят о наклонном круглом цилиндре. Если же генератриса будет перпендикулярна плоскостям основания, то цилиндр называется прямым. Он показан на рисунке ниже.

Здесь AB = DC — радиус цилиндра, AD = BC = h — высота фигуры. Для прямого цилиндра высота всегда равна длине образующей. Отрезок AD обозначает ось цилиндра — прямая, соединяющая две центральные точки оснований. От оси цилиндра все точки боковой поверхности лежат на одном расстоянии, равном радиусу фигуры.

Далее в статье будем рассматривать развертку поверхности цилиндра, круглого и прямого.

Видео:ОБЪЕМ ЦИЛИНДРА #shorts #егэ #огэ #математика #профильныйегэСкачать

Развертка круглого прямого цилиндра

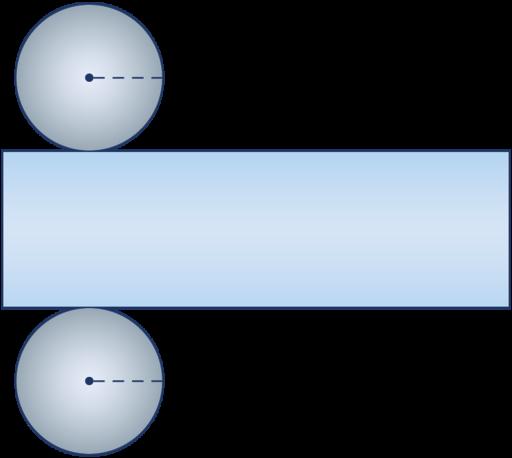
Когда говорят о развертке цилиндра, то подразумевают общую площадь его поверхности, представленную плоскими фигурами. Круглый прямой цилиндр образован двумя кругами, имеющими одинаковые радиусы, и одной боковой поверхностью, которая эти круги соединяет друг с другом.

На рисунке показан бумажный цилиндр. Как осуществляется построение развертки цилиндра? Возьмем воображаемые ножницы и отрежем одно основание вдоль окружности. Затем проделаем аналогичные действия со вторым основанием. Боковую поверхность разрежем вдоль генератрисы, то есть параллельно оси фигуры, и развернем ее. Таким образом, мы получили развертку, которая показана на рисунке ниже.

Очевидно, что она состоит из двух одинаковых кругов. Что касается цилиндрической поверхности, то в разрезанном виде она представлена прямоугольником. Развертку удобно использовать при определении площади поверхности рассматриваемой фигуры.

Видео:Цилиндр, конус, шар, 6 классСкачать

Площадь развертки цилиндра

Выше мы показали, как можно получить развертку фигуры. Чтобы рассчитать ее площадь, необходимо сложить площади для всех ее частей, то есть для двух круглых оснований и одного прямоугольника.

Обозначим радиус основания буквой r, а высоту фигуры — буквой h. Площадь одного основания равна площади круга, то есть:

Здесь pi — число Пи, приблизительно равное 3,14.

Чтобы вычислить площадь прямоугольника, представляющего боковую поверхность фигуры в развернутом виде, необходимо знать две его стороны. Одна из них равна высоте h. Вторая, как можно догадаться, соответствует длине директрисы, то есть длине окружности. Обозначим ее l. Тогда можно записать следующие равенства:

Здесь S_b — площадь прямоугольника, равная площади цилиндрической поверхности.

Учитывая, что фигура имеет два основания, складываем рассчитанные величины, получаем общую площадь развертки цилиндра:

Площадь S фигуры однозначно определяется через ее радиус и высоту.

Покажем, как использовать это равенство для решения геометрической задачи.

Видео:VFXLAB: 3D ТРЮКИ. КРУГИ И ЦИЛИНДРЫ.Скачать

Задача на нахождение радиуса фигуры

Известно, что общая поверхность круглого прямого цилиндра составляет 60 см 2 . Чему равен радиус основания цилиндра, если его высота равна 7 см, а фигура имеет лишь одно основание.

Описанный в условии задачи цилиндр представляет собой бочку без крышки, поэтому площадь его поверхности образована не двумя, а одним основанием.

Если учесть названный факт, тогда формула для площади фигуры запишется в следующем виде:

Подставим все известные из условия величины в это равенство, получим:

Мы получили классическое полное квадратное уравнение. Его решение даст искомое значение радиуса r. Решаем через дискриминант:

При решении уравнения отрицательный корень был отброшен, в виду его нефизического значения.

Таким образом, параметры открытого цилиндра из условия задачи составляют 7 см в высоту и 2,5 см в диаметре.

💥 Видео

Хон или зеркало? Научно-практический коментарийСкачать

ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

Тела вращения. Урок 1 Цилиндр.Конус.Шар.Скачать

Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Обзор ручного хонаСкачать

СВОИМИ РУКАМИ: Хонинговка цилиндраСкачать

60. Площадь поверхности цилиндраСкачать