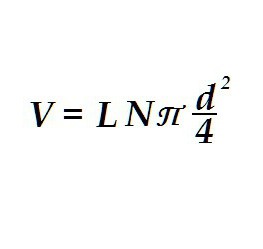Как называется цилиндр с отверстием в центре

Видео:Видеоурок по математике "Цилиндр"Скачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:9 класс, 41 урок, ЦилиндрСкачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:ЭВОЛЮЦИЯ В МИРЕ ЦИЛИНДРА ( The Eternal Cylinder )Скачать

Основные элементы цилиндра

• Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
• R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
• O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
• l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

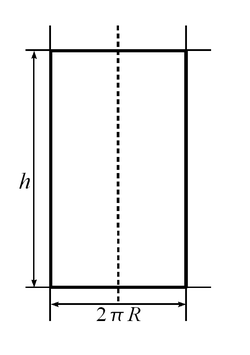
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

• длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
• ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:КАК ИЗМЕРИТЬ ЦИЛИНДРЫ? Учимся пользоваться нутромером и микрометромСкачать

Геометрические тела. Цилиндр.

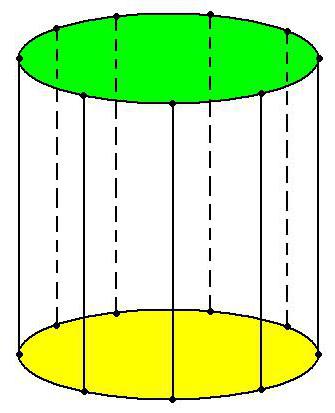
Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

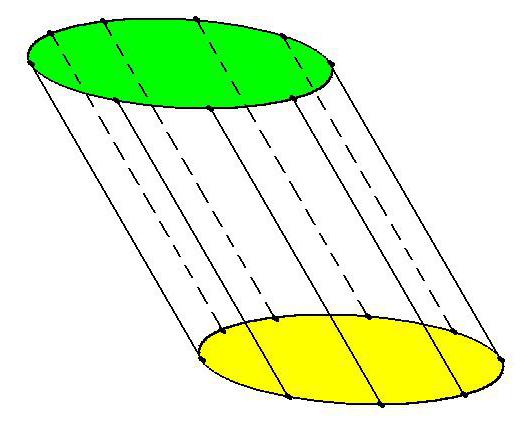
Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:Гидравлические соединения. Штуцера, Уголки и Тройники для РВДСкачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

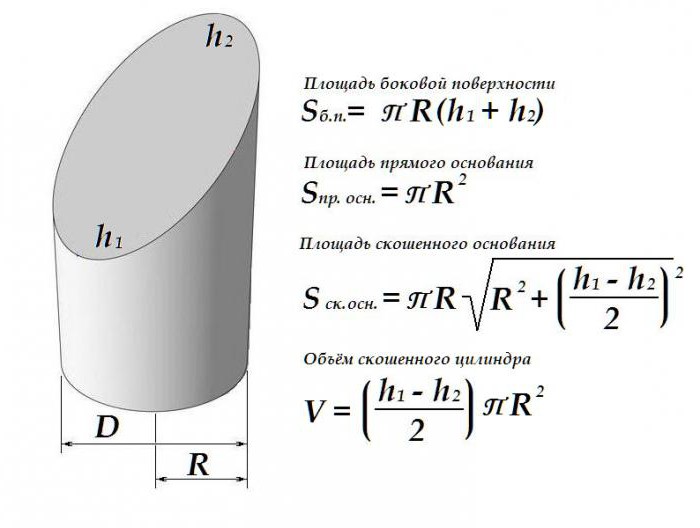
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:Безумный способ открыть любой замок без ключа!Удивительный трюк со спичками,который отлично работаетСкачать

Цилиндр

Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей.

В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.

Другие виды цилиндра — (по наклону образующей) косой или наклонный (если образующая касается основания не под прямым углом); (по форме основания) эллиптический, гиперболический, параболический.

Призма также является разновидностью цилиндра — с основанием в виде многоугольника.

Видео:Допуски и посадки для чайников и начинающих специалистовСкачать

Площадь поверхности цилиндра

Площадь боковой поверхности

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой и длиной , равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

В частности, для прямого кругового цилиндра:

, и

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма, к сожалению, не существует.

Площадь полной поверхности

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:

Видео:ОБЪЯСНЕНИЕ МИРА, ОТКУДА ПРИШЕЛ ЦИЛИНДР ( The Eternal Cylinder )Скачать

Объём цилиндра

Для наклонного цилиндра существуют две формулы:

• Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей. ,
• Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания): ,

где — длина образующей, а — угол между образующей и плоскостью основания. Для прямого цилиндра .

Для прямого цилиндра , и , и объём равен:

Видео:НОВАЯ ТЕХНОЛОГИЯ ЦИЛИНДРА ( The Eternal Cylinder )Скачать

Примечания

Wikimedia Foundation . 2010 .

цилиндр — а, м. cylindre m., нем. Zylinder <, лат. cylindrus <гр. 1. Геометрическое тело, образуемое вращение прямоугольника вокруг одной из его сторон. Объем цилиндра. БАС 1. Толстота цилиндра равна площади его основанья, помноженной на высоту. Даль … Исторический словарь галлицизмов русского языка

ЦИЛИНДР — муж., греч. прямая стопка, вал; облец, обляк; тело, ограниченное с концов двумя кругами, а с боков гнутою по кругам плоскостью. Толстота цилиндра равна площади его основанья, помноженной на высоту, геом. Паровой цилиндр, халява, труба, в которой… … Толковый словарь Даля

цилиндр — цилиндрическая поверхность, барабан, вал; шапокляк, шляпа, ролик, рол, дорн, цилиндрик, пойнт, царга, тело, вальц Словарь русских синонимов. цилиндр сущ., кол во синонимов: 22 • атактостела (2) … Словарь синонимов

ЦИЛИНДР — (от греч. kylindros) в элементарной геометрии геометрическое тело, образованное вращением прямоугольника около одной стороны: объем цилиндра V=?r2h, а площадь боковой поверхности S = 2?rh. Боковая поверхность цилиндра есть часть цилиндрической… … Большой Энциклопедический словарь

ЦИЛИНДР — полая деталь с цилиндрической внутренней поверхностью, в которой движется поршень. Одна из основных деталей поршневых машин и механизмов … Большой Энциклопедический словарь

ЦИЛИНДР — высокая мужская шляпа из шелкового плюша с небольшими твердыми полями … Большой Энциклопедический словарь

ЦИЛИНДР — ЦИЛИНДР, твердое тело или поверхность, образуемые вращением прямоугольника вокруг одной из его сторон в качестве оси. Объем цилиндра, если обозначить его высоту как h, а радиус основания как r, равен pr2h, а площадь изогнутой поверхности 2prh … Научно-технический энциклопедический словарь

ЦИЛИНДР — ЦИЛИНДР, цилиндра, муж. (от греч. kylindros). 1. Геометрическое тело, образуемое вращением прямоугольника около одной из его сторон, называемой осью, и имеющее в основаниях круг (мат.). 2. Часть машин (двигателей, насосов, компрессоров и т.д.) в… … Толковый словарь Ушакова

ЦИЛИНДР — ЦИЛИНДР, а, муж. 1. Геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон. 2. Колонновидный предмет, напр. часть поршневой машины. 3. Высокая твёрдая шляпа такой формы с небольшими полями. Чёрный ц. | прил.… … Толковый словарь Ожегова

ЦИЛИНДР — (Steam cylinder) одна из основных деталей поршневых машин. Выполняется в виде полого круглого Ц., в котором движется поршень. Ц. паровых машин снабжается обычно паровой рубашкой для обогревания его стенок в целях уменьшения конденсации пара.… … Морской словарь

Видео:Про суппорта и направляющиеСкачать

Цилиндр. Виды, объём цилиндра, площадь поверхности

Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.

Планиметрия – раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье – цилиндр.

Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже – коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец – знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.

Видео:СЕКРЕТ ЦИЛИНДРА ( The Eternal Cylinder )Скачать

Определение цилиндра как геометрической фигуры

Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».

Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами – усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.

Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра – один из элементов данной геометрической фигуры. Другая её важная составляющая – рассмотренные выше круги. Называются они основаниями.

Видео:СЛУГА БЕСКОНЕЧНОГО ЦИЛИНДРА Eternal Cylinder PartnerСкачать

Виды цилиндров

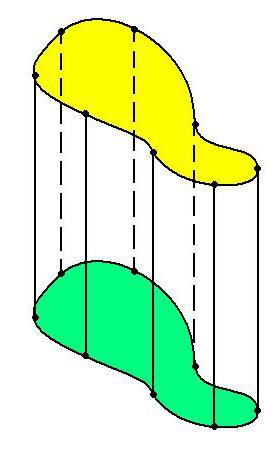
Самый простой и распространённый вид цилиндра – круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.

Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.

По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр – наклонный.

Видео:Микрометр и нутромер. Как измерить цилиндры?Скачать

Что такое поверхность вращения

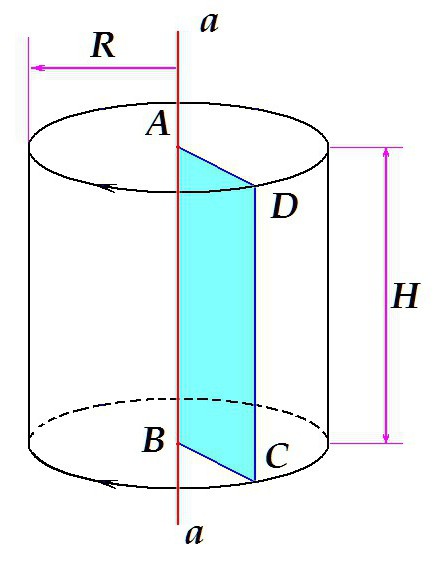
Прямой круговой цилиндр, без сомнения – самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.

Допустим, имеется некая прямая a, расположенная вертикально. ABCD – прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a. Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения – прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.

В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг – шар и т.д.

Видео:Видео по запросу: отверстия в цилиндреСкачать

Площадь поверхности цилиндра

Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.

Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.

Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.

Видео:ПЕРЕЛЕЗЛИ ЧЕРЕЗ ЦИЛИНДР ( The Eternal Cylinder )Скачать

Определение объёма фигуры

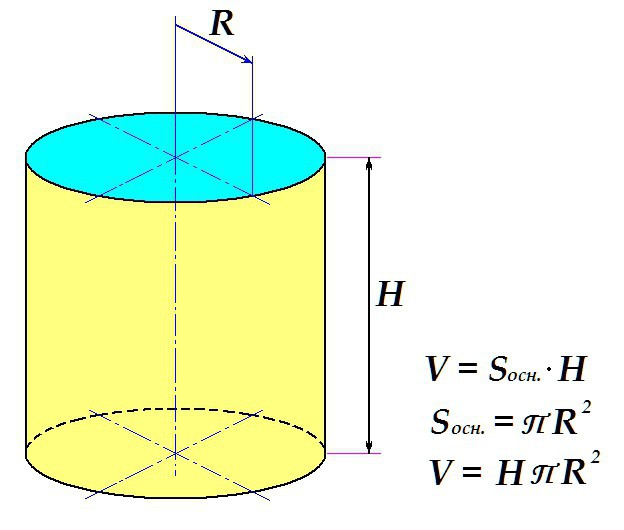
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.

Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.

Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.

Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.

Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.

Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.

Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними.

Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.

Видео:ЯРОСТЬ ЦИЛИНДРА ( The Eternal Cylinder )Скачать

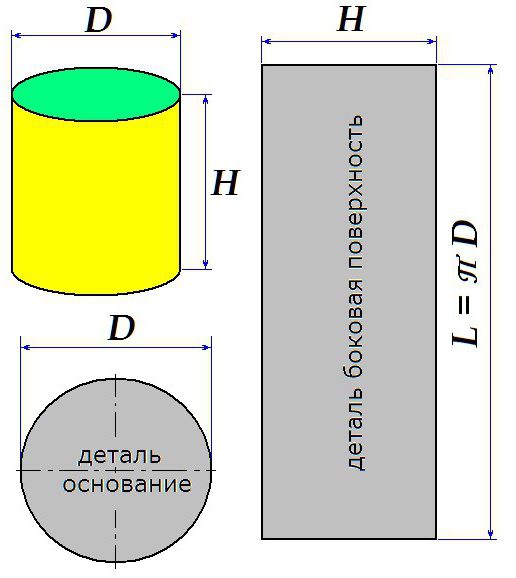
Как построить развёртку цилиндра

В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.

Следует учитывать, что рисунок приведен без учёта швов.

Видео:Цилиндр с вырезомСкачать

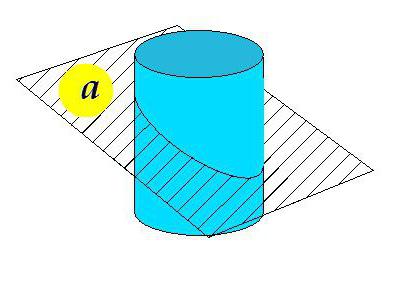
Отличия скошенного цилиндра

Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.

На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.

Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.

Видео:Уроки Компас 3D.Развертка цилиндраСкачать

Геометрические характеристики скошенного цилиндра

Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.

📹 Видео

Закон БернуллиСкачать