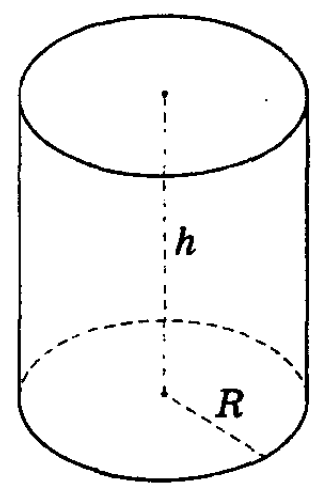
Как называются отрезки соединяющие соответствующие точки окружности в цилиндре (8 видео)

Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.

Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.

Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.

Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.

Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.

Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.

Круговой цилиндр — цилиндр, основания которого являются кругами.

Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.

Радиус цилиндра – радиус его основания.

Образующая цилиндра — образующая цилиндрической поверхности.

Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.

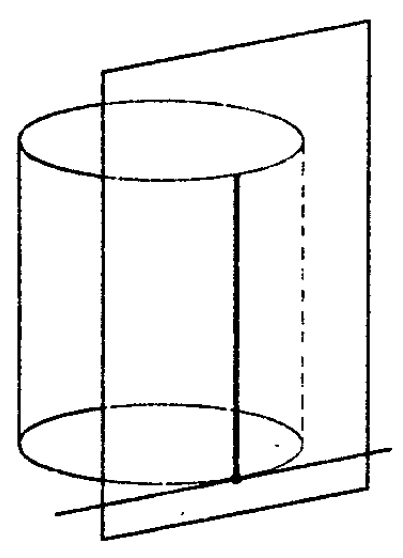
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.

Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.

Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_ =2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.

Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_ =2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.

Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).

Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.

Содержание

Стереометрия. Страница 6
1. Цилиндр
Сечение цилиндра плоскостями
2.Конус
Сечение конуса плоскостями
3. Вписанная и описанная призма
4.Вписанная и описанная пирамида
5. Шар
Сечение шара плоскостью
6. Симметрия шара
7. Пример 1
Пример 2
Пример 3
Пример 4
Пример 5
🎦 Видео

Видео:Видеоурок по математике "Цилиндр"Скачать

Стереометрия. Страница 6

Видео:Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

1. Цилиндр

Цилиндр представляет собой тело, состоящее из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (Рис.1).

Два круга, лежащих в параллельных плоскостях, называются основаниями цилиндра. Отрезки, соединяющие соответствующие точки окружностей кругов, называются образующими.

Читайте также: Внутри цилиндра может двигаться поршень

Так как основания совмещаются параллельным переносом, то они равны. И так как они лежат в параллельных плоскостях, то образующие цилиндра параллельны и равны.

Если образующие перпендикулярны основанию, то цилиндр называется прямым.

Поверхность цилиндра состоит из двух оснований и боковой поверхности. Боковая поверхность состоит из образующих.

Осью цилиндра называется прямая, проходящая через центры оснований. Радиусом цилиндра называется радиус его основания. А высотой цилиндра называется расстояние между плоскостями его оснований.

Видео:Как искать точки на тригонометрической окружности.Скачать

Сечение цилиндра плоскостями

Если взять сечение цилиндра плоскостью, проходящей по его оси, то получится прямоугольник. (Рис.1) Такое сечение называется осевым. Сечение цилиндра плоскостью, параллельной его оси, также представляет собой прямоугольник. Две его стороны — образующие цилиндра, а две другие стороны — параллельные хорды оснований.

Теорема. Плоскость сечения цилиндра, параллельная его плоскости основания, пересекает его боковую поверхность по окружности, равной окружности основания. (Рис.1.1)

Пусть плоскость α — секущая плоскость, параллельная основанию. Подвергнем плоскость α движению в верх вдоль оси цилиндра. Параллельным переносом совместим плоскость α с плоскостью верхнего основания цилиндра. Таким образом сечение боковой поверхности совпадет с окружностью верхнего основания. Теорема доказана.

Рис. 1.1 Сечения цилиндра плоскостями.

Видео:Геометрия 9 класс (Урок№34 - Тела и поверхности вращения.)Скачать

2.Конус

Конусом называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости основания этого конуса — вершины конуса и всех отрезков, соединяющих вершину с точками основания (Рис.2).

Точка, не лежащая в плоскости основания, называется вершиной конуса. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.

Конус называется прямым, если прямая, проведенная из вершины конуса в центр основания, перпендикулярна плоскости основания.

Высотой конуса называется перпендикуляр, опущенный из вершины конуса на плоскость основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.

Видео:ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

Сечение конуса плоскостями

Сечение прямого конуса плоскостью, которая проходит через его вершину, представляет собой равнобедренный треугольник. Боковые стороны этого треугольника являются образующими конуса. Сечение, которое проходит через ось конуса, называется осевым.

Теорема. Сечение конуса плоскостью, параллельной основанию, есть круг с центром на оси конуса.

Доказательство. Пусть α — плоскость, параллельная основанию (Рис 2.1). Плоскость α пересекает конус по кругу. Подвергнем сечение конуса гомотетии относительно вершины конуса. Т.е. совместим плоскость α с плоскостью основания конуса. Сечение конуса полностью совпадет с основанием. Следовательно сечение конуса плоскостью есть круг, а сечение боковой поверхности — окружность с центром на оси конуса.

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

3. Вписанная и описанная призма

Призма, вписанная в цилиндр, называется призма, у которой плоскости основания совпадают с плоскостями оснований цилиндра, а боковые ребра являются образующими цилиндра.

Призма, описанная около цилиндра, называется призма, у которой плоскости оснований совпадают с плоскостями оснований цилиндра, а боковые грани касаются цилиндра (Рис.3).

Если плоскость проходит через образующую цилиндра и перпендикулярна осевому сечению, то она называется касательной плоскостью к цилиндру.

Рис. 3 Описанная и вписанная призма.

Видео:Виды и изометрия цилиндраСкачать

4.Вписанная и описанная пирамида

Пирамида, вписанная в конус, называется пирамида, у которой вершина совпадает с вершиной конуса, а многоугольник в основании вписан в окружность основания конуса.

Читайте также: Замена штуцера главного цилиндра сцепления ваз 2105

Пирамидой, описанной около конуса, называется пирамида, у которой вершина совпадает с вершиной конуса, а в многоугольник основания вписано основание окружности конуса.

Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса (плоскость α) и перпендикулярная плоскости осевого сечения (плоскость β), проходящей через эту образующую (Рис.4).

Рис. 4 Вписанная и описанная пирамида.

Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

5. Шар

Шар это геометрическое тело, состоящее из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. (Рис.5). Точка, от которой все остальные точки находятся на расстоянии не большем данного, называется центром шара.

Граница шара называется сферой. Совокупность всех точек сферы удалена от центра на расстояние, равное радиусу. Таким образом, любой отрезок, соединяющий центр шара с точкой сферы, называется радиусом.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Видео:РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Сечение шара плоскостью

Если секущая плоскость проходит через центр шара, например плоскость α, то она называется диаметральной плоскостью. А сечение называется большим кругом (Рис.5.1).

Если секущая плоскость не проходит через центр шара, то в сечении получится также круг. Сформулируем следующую теорему.

Теорема. Любое сечение шара представляет собой круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Пусть β — секущая плоскость. Проведем перпендикуляр из центра шара точки O на плоскость β. Обозначим основание перпендикуляра точкой O’.

Рис. 5.1 Сечение шара плоскостью.

Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

6. Симметрия шара

Теорема. Центр шара является его центром симметрии, а любая диаметральная плоскость является его плоскостью симметрии.

Доказательство. Пусть α — диаметральна плосксоть шара, а Y его произвольная точка (Рис.6). Построим точку Y’, симметричную точке Y относительно плоскости α. Так как отрезок YY’ перпендикулярен плоскости α и делится этой плоскостью пополам точкой пересечения А, то треугольники OYA и OY’A равны по двум сторонам и углу между ними, т.е. OY=OY’. Отрезки OY и OY’ принадлежат шару, так как OY = OY’ ≤ R.

Отложим отрезок OY» симметрично относительно центра шара точки О. Тогда OY = OY» ≤ R. Т.е. точка Y» также принадлежит шару. Следовательно точка О является точкой симметрии шара, а диаметральная плоскость — плоскостью симметрии.

7. Пример 1

Радиус основания цилиндра 2 м, высота 3 м. Найдите диагональ осевого сечения.

Пусть дан цилиндр высотой 3 м и радиусом 2 м (Рис.7). По теореме Пифагора найдем АС:

AС 2 = AD 2 + CD 2 = 4 2 + 3 2 = 25

Рис.7 Задача. Радиус основания цилиндра 2 м.

Пример 2

Высота цилиндра 6 м, радиус основания 5 м. Концы отрезка DC’, длина которого 10 м, лежат на окружностях оснований. Найдите расстояние от этого отрезка до оси цилиндра.

Пусть дан цилиндр высотой 6 м с радиусом основания 5 м и отрезком DC’ = 10 м (Рис. 8). Проведем два перпендикуляра C’C и D’D. Так как эти перпендикуляры параллельны, то проведем через них плоскость α. Теперь проведем плоскость β через ось O’O, параллельную плоскости α.

Таким образом, получается, что через две скрещивающиеся прямые OO’ и DC’ проходят две параллельные плоскости α и β. Расстояние между скрещивающимися прямыми равно расстоянию между двумя параллельными плоскостями, в которых эти прямые лежат.

Читайте также: Как поменять блок цилиндр в двигателе

Отсюда следует, что длина перпендикуляра ОЕ и будет расстояние от отрезка DC’ до оси цилиндра OO’.

Найдем хорду DC из прямоугольного треугольника DC’C:

DC 2 = 10 2 — 6 2 = 64, DC = 8 м.

Теперь из прямоугольного треугольника OED найдем ОЕ:

ОЕ 2 = OD 2 — DE 2 = 5 2 — 4 2 = 9

Рис.8 Задача. Высота цилиндра 6 м.

Пример 3

Высота конуса 20 м, радиус основания 25 м. Найдите площадь сечения, проведенного через вершину, если расстояние от него до центра основания конуса равно 12 м.

Пусть дан конус высотой 20 м с радиусом основания 25 м. OF = 12 м (Рис. 9). Найдем синус угла OSF из прямоугольного треугольника OSF.

sin OSF = OF / SO = 12 / 20 = 3/5, следовательно, cos OSF = 4/5

Из прямоугольного треугольника OSC найдем SC:

cos OSC = SO / SC, SC = SO / cos OSC = 20/4/5 = 25 м

По теореме Пифагора найдем ОС:

ОC 2 = SC 2 — SO 2 = 25 2 — 20 2 = 225, OC = 15 м.

Из прямоугольного треугольника АОС найдем АC:

АC 2 = АО 2 — ОС 2 = 25 2 — 15 2 = 400, АC = 20 м.

Таким образм, площадь сечения равна:

S_ASB = AC * SC = 20 * 25 = 500 м 2 .

Рис.9 Задача. Высота конуса 20 м.

Пример 4

Высота конуса 10 м. Радиус основания 6 м. На каком расстоянии от вершины необходимо провести плоскость, параллельную основанию, чтобы площадь сечения была равна половине площади основания.

Пусть дан конус высотой 10 м и радиусом основания 6 м (Рис. 10). Обозначим площадь основания как S_б, а площадь сечения как S_м. Найдем площадь большего основания S_б:

S_б = π R 2 = π 6 2 = 36π м 2

Соответственно площадь малого основания S_м будет равна:

S_м = S_б / 2 = 36π / 2 = 18π м 2

Отсюда, радиус сечения СА равен

Рассмотрим треугольники BOS и CAS. Они подобны. Коэффициент подобия составляет k = CA / BO = / 6

Отсюда следует, что SA = k SO = 10 / 6 = 5 м

Таким образом, для того чтобы площадь сечения составляла половину площади основания, расстояние от вершины конуса до плоскости сечения должно составлять 5 м.

Рис.10 Задача. Высота конуса 10 м.

Пример 5

Радиусы оснований усеченного конуса 4 м и 12 м, образующая 10 м. Найдите площадь осевого сечения.

Пусть дан усеченный конус. Образующая АС = 10 м и радиусы оснований СЕ = 4 м, АО = 12 м (Рис. 11). Осевое сечение усеченного конуса представляет собой равнобокую трапецию. Отсюда следует, что площадь сечения можно найти как сумму площадей прямоугольника CFTP и двух равных треугольников АСР и TFB.

Найдем площадь двух треугольников АСР и TFB:

По теореме Пифагора найдем СР:

СР 2 = AC 2 — AР 2 = 10 2 — 8 2 = 36, CP = 6 м

S_ACP + S_TFP = 2 S_ACP = 2 * АР * СР / 2 = 2 * 8 * 6 / 2 = 48 м 2

Теперь найдем площадь прямоугольника S_CFTP:

S_CFTP = CF * CP = 2 CE * CP = 2 * 4 * 6 = 48 м 2

Таким образом, площадь сечения усеченного конуса составляет:

S_АCFВ = S_CFTP + 2 S_ACP = 48 + 48 = 96 м 2 .