Как объем цилиндра при известном объеме конуса

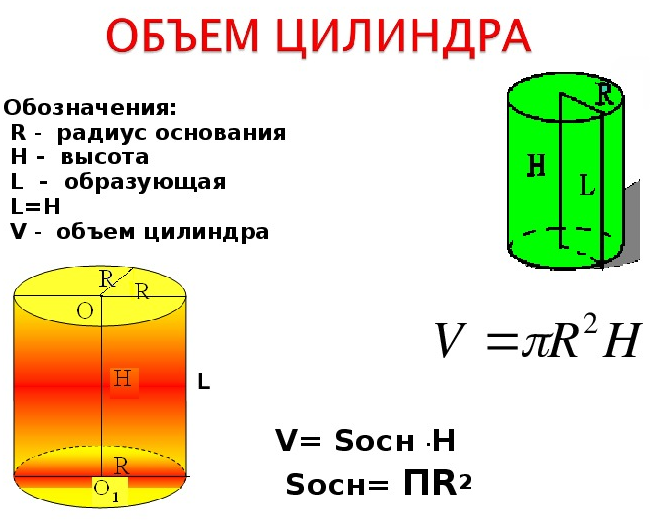
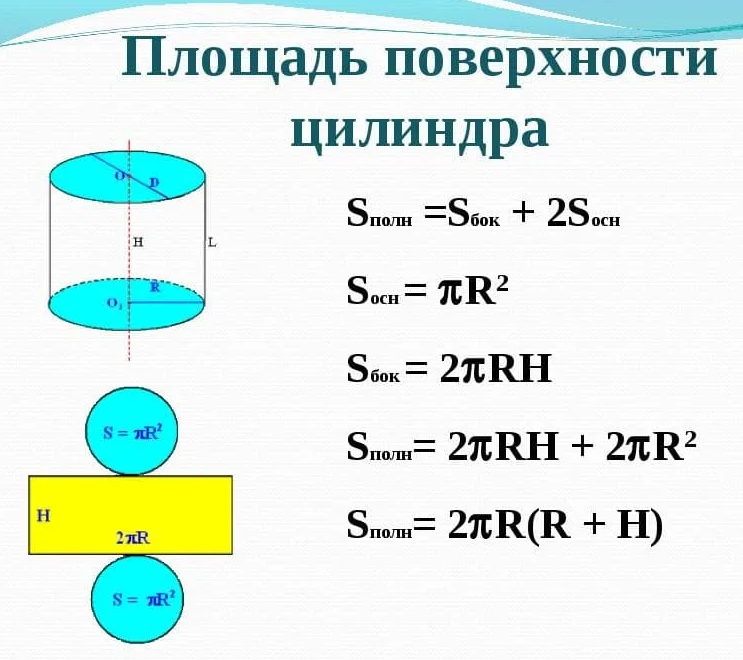
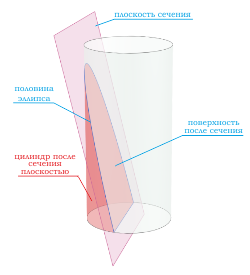
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Видео:11 класс. Геометрия. Объем конуса. 21.04.2020Скачать

Объем правильного цилиндра через радиус и высоту цилиндра

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

Видео:Объём цилиндраСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

Видео:Объем цилиндраСкачать

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Видео:Цилиндр, конус, шар, 6 классСкачать

Поверхности цилиндра

Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.

Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.

Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Читайте также: Порядок работы цилиндров бмв м20

Видео:11 класс, 32 урок, Объем цилиндраСкачать

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях:

Видео:Усеченный конус. 11 класс.Скачать

Урок 6 Объем цилиндра Объем конуса Объем усеченного конуса Объем шара Задачи. — презентация

Презентация была опубликована 6 лет назад пользователемВероника Ледицкая

Похожие презентации

Видео:Конус. 11 класс.Скачать

Презентация на тему: » Урок 6 Объем цилиндра Объем конуса Объем усеченного конуса Объем шара Задачи.» — Транскрипт:

2 Объем цилиндра Объем конуса Объем усеченного конуса Объем шара Задачи

7 1 Найдите объем цилиндра, если радиус основания равен 2 см, а высота 5 см. V= r 2 h 20 см 3

8 2 Найдите объем конуса, если его высота 3 см, а радиус основания 4 см. 16 см 3

9 3 Найти объем усеченного конуса, если его высота 5 см,а радиусы оснований 4 см и 2 см.

10 4 Найти объем шара, если его радиус 10 см.

11 Найдите объем кошки Мурки, если после окунания ее в ведро с водой в ведре осталось 6 л воды, а до окунания было 8,5 л. 5 2,5 л

12 Найдите объем бункера с зерном, если его высота 7 м, высота конической части 2 м, а диаметр 4 м. 4 м 2 м 6 7 м

13 h=7-2=5(м) V ц = 20 (м 3 ) 4 м 2 м 6. Решение. V ц = r 2 h Ответ: V=V ц +V к 7 м r=2 м

14 Объем конуса равен одной трети произведения площади основания на высоту. Иначе говоря, объем конуса выражается следующей формулой: Существует много доказательств этой формулы, рассмотрим некоторые из них.

15 Первое доказательство. За величину объёма конуса принимается предел, к которому стремится объем правильной пирамиды, вписанной в конус, при неограниченном удвоении числа сторон её основания.

16 Второе доказательство: Сечение конуса плоскостью, параллельной основанию, подобно основанию. Если плоскость проходит на расстоянии х от вершины, то коэффициент подобия равен Поэтому площадь сечения S(x) такой плоскостью равна: где S — площадь основания. Значит, объем конуса К будет: H S осн S сеч x

17 Третье доказательство: 0 x y H α R У=kx Задание. Исходя из своих возможностей, выберите хотя бы одно доказательство и уметь отвечать.

18 «Знаете ли, Вы…» «Конусами» называется род брюхоногих моллюсков отряда переднежаберных, группы стрелоязычных, семейства конусовых. Раковина коническая (2-16 см), ярко окрашенная. Конусов свыше 520 видов. Живут в теплых морях, особенно в Вест–Индии и около Америки. Некоторые съедобны, другие ценятся благодаря красоте раковины. В геологии существует понятие «конус выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину. В биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.

Читайте также: Длинный цилиндр радиусом равномерно заряжен по поверхности с плотностью

19 По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на жителей (чаще в южных странах). Чтобы этого не случалось, устанавливают молниеотводы, которые образуют конус безопасности. Чем выше молниеотвод, тем больше объем такого конуса. Некоторые люди пытаются спрятаться от разрядов под деревом, но дерево не проводник, на нем разряды накапливаются, и дерево может быть источником напряжения. В физике встречается понятие «телесный угол». Это конусообразный угол, вырезанный в шаре. Единица измерения телесного угла – 1 стерадиан. 1 стерадиан – это телесный угол, квадрат радиуса которого равен площади части сферы, которую он вырезает. Если в этот угол поместить источник света в 1 канделу (91 свечу), то получим световой поток в 1 люмен. Свет от киноаппарата или прожектора распространяется в виде конуса. «Знаете ли, Вы…» «Знаете ли, Вы…»

20 Задача *. Докажите геометрически, что если бы какой-нибудь древний деспот вздумал осуществить такую затею, он был бы обескуражен мизерностью результата. Перед ним высилась бы настолько жалкая кучка земли, что никакая фантазия не смогла бы раздуть ее в легендарный «гордый холм». 1 горсть 0,2 дм 3 Войско в воинов считалось очень внушительным. Угол откоса 45 0, иначе земля начнет осыпаться. В своем драматическом произведении «Скупой рыцарь» Александр Сергеевич Пушкин рассказывает одну старинную легенду восточных народов: «… Читал я где-то, Что царь однажды воинам своим Велел снести земли по горсти в кучу. И гордый холм возвысился, И царь мог с высоты с весельем озирать И дол, покрытый белыми шатрами, И море, где бежали корабли.» Это одна из немногих легенд, в которой, при кажущемся правдоподобии, нет и зерна правды.

21 Решение к задаче *. V=0, =20 000(дм 3 )=20(м 3 ). Так как H=R, то V=1/3πH 3. Ответ: 2,7 метров.

22 Надо обладать очень богатым воображением, чтобы земляную кучу в 2,7 м (1,5 человеческого роста) назвать «гордым холмом». Сделав расчет для меньшего угла, мы получили бы еще более скромный результат. У Аттилы было самое многочисленное войско, которое знал древний мир. Историки оценивают его в человек. Если бы даже все воины Аттилы участвовали в насыпании холма, образовалась бы куча повыше вычисленной нами, но не очень. Домашнее задание. п. 66, 67, , 705, 713 Попробуйте сами дома вычислить высоту такого кургана и подумать, удовлетворила ли бы такая высота честолюбие Аттилы или нет?

23 «Наука изощряет ум; ученье вострит память.» Козьма Прутков Козьма Прутков

Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Как объем цилиндра при известном объеме конуса

119. Определения. 1) За величину объёма цилиндра принимается предел, к которому стремится объём правильной призмы, вписанной в цилиндр, когда число боковых граней этой призмы неограниченно удваивается.

Читайте также: Как восстановить сорванную резьбу в блоке цилиндров

2) За величину объёма конуса (полного или усечённого) принимается предел, к которому стремится объём правильной пирамиды (полной или усечённой), когда число боковых граней пирамиды неограниченно удваивается.

120. Теоремы. 1) Объём цилиндра равен произведению площади основания на высоту.

2) Объём конуса равен произведению площади основания на треть высоты.

Впишем в цилиндр какую-нибудь правильную призму, а в конус— какую-нибудь правильную пирамиду; тогда, обозначив площадь основания призмы или пирамиды буквой В₁, высоту их буквой Н и объём — V₁ получим:

Вообразим теперь, что число боковых граней призмы и пирамиды неограниченно удваивается. Тогда В₁ будет иметь пределом площадь В основания цилиндра или конуса, а высота Н остаётся без изменения; значит, произведения В₁Н и 1 /₃ В₁Н будут стремиться к пределам ВН и 1 /₃ВН, и потому объём V цилиндра или конуса будет:

для цилиндра V = ВН;
для конуса V = 1 /₃ ВН.

121. Следствие. Если радиус основания цилиндра или конуса обозначим через R, то В = πR 2 , поэтому

объём цилиндра V = πR 2 Н;
объём конуса V = 1 /₃ πR 2 Н.

122. Теорема. Объём усечённого конуса равен сумме объёмов трёх конусов, имеющих одинаковую высоту с усечённым конусом, а основаниями: один — нижнее основание этого конуса, другой — верхнее, третий— круг, площадь которого есть среднее геометрическое между площадями верхнего и нижнего оснований.

Теорему эту докажем совершенно так же, как раньше мы доказали теорему для объёма усечённой пирамиды (§ 92).

На верхнем основании усечённого конуса (черт. 134) поместим такой малый конус (с высотой h), который дополняет данный усечённый конус до полного.

Тогда объём V усечённого конуса можно рассматривать как разность объёмов полного конуса и дополнительного. Поэтому

Из подобия треугольников находим: .

Так как πR 2 выражает площадь нижнего основания, πr 2 —площадь верхнего основания и πRr = √ πR 2 • πr 2 есть среднее геометрическое между площадями верхнего и нижнего оснований, то полученная нами формула вполне подтверждает теорему.

Видео:Объем цилиндра.Скачать

Нахождение объема цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.

Видео:Видеоурок по математике "Цилиндр"Скачать

Формула вычисления объема цилиндра

Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R 2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

Видео:Объем цилиндра.Скачать

Примеры задач

Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см 2 , а также, высота – 10 см.

Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .

Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.

Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .

📹 Видео

Объем конуса. Объем усеченного конуса.Скачать

Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

11 класс, 17 урок, Площадь поверхности конусаСкачать

ЦИЛИНДР. КОНУС. ШАР. ЕГЭ. ЗАДАНИЕ 5.СТЕРЕОМЕТРИЯСкачать

Объем конуса. Практическая часть. 11 класс.Скачать

ЦИЛИНДР. КОНУС. ШАР.Скачать

Вычисление объёма цилиндраСкачать