- Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
- Геометрическая фигура
- Прямой и наклонный цилиндры
- Осевое сечение прямого цилиндра
- Осевое сечение наклонного цилиндра
- Задача с прямым цилиндром
- Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
- Геометрическая фигура
- Прямой и наклонный цилиндры
- Осевое сечение прямого цилиндра
- Осевое сечение наклонного цилиндра
- Задача с прямым цилиндром
- Что такое цилиндр: определение, элементы, виды, варианты сечения
- Определение цилиндра
- Основные элементы цилиндра
- Диаметр и диагональ цилиндра
- Свойства
- 🔥 Видео
Видео:№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
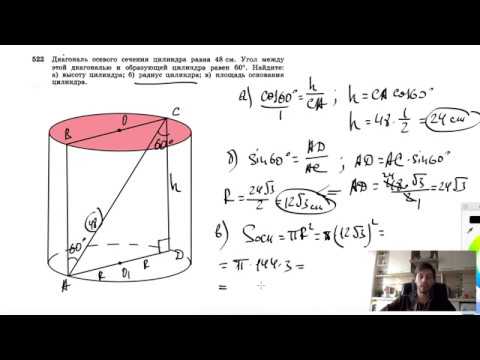
Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
Цилиндр — это симметричная пространственная фигура, свойства которой рассматривают в старших классах школы в курсе стереометрии. Для его описания используют такие линейные характеристики, как высота и радиус основания. В данной статье рассмотрим вопросы касательно того, что такое осевое сечение цилиндра, и как рассчитать его параметры через основные линейные характеристики фигуры.
Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Геометрическая фигура
Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.
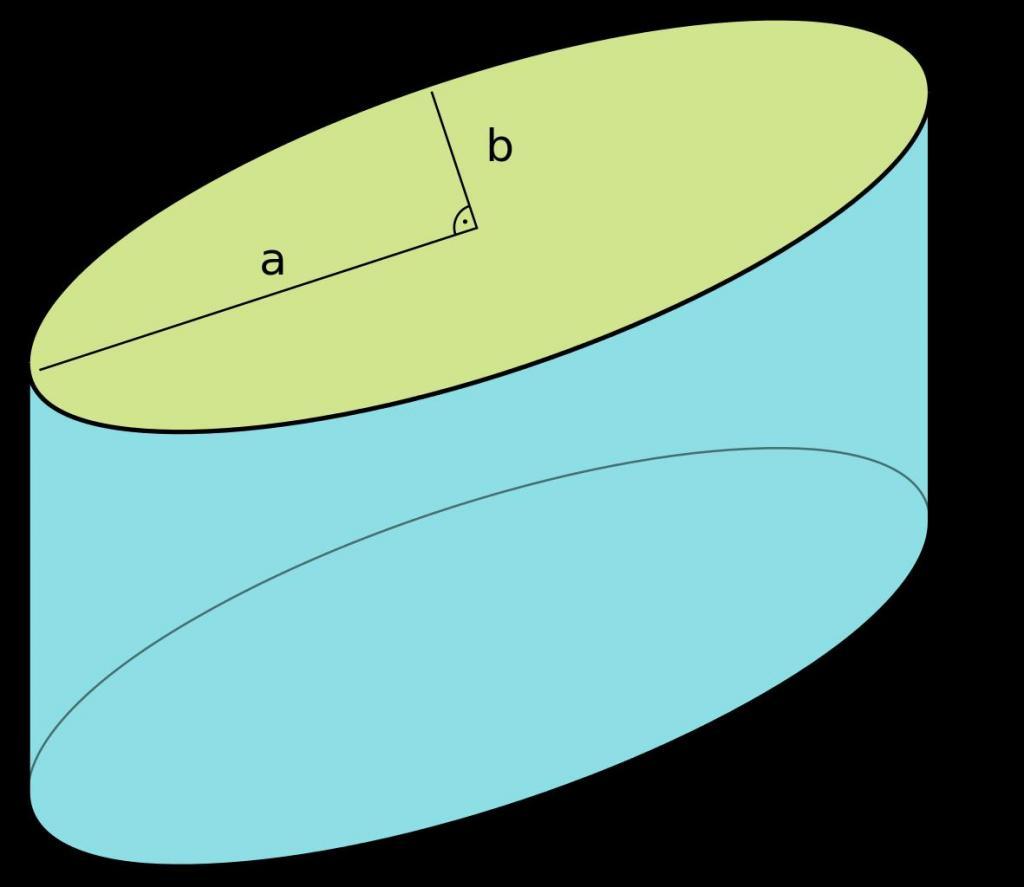
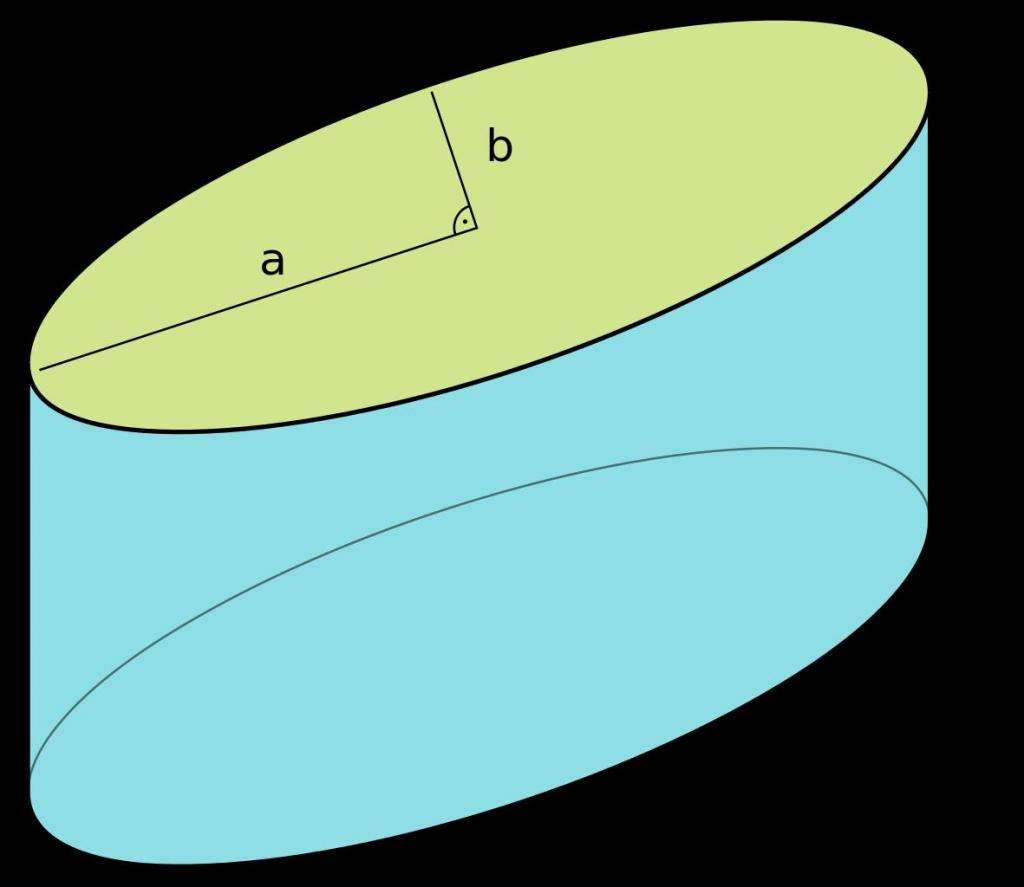
На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.
Здесь отрезок длиной h является его образующей и высотой.
Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.
Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Прямой и наклонный цилиндры
Перед тем как переходить к рассмотрению осевого сечения цилиндров, расскажем, какие типы этих фигур бывают.
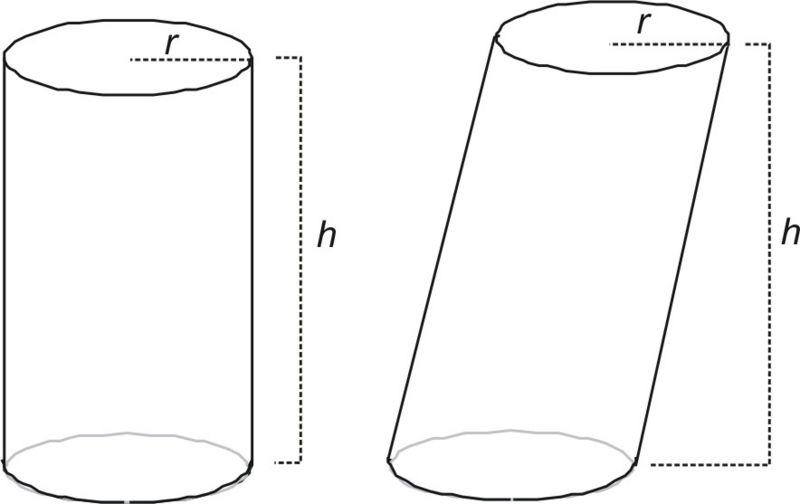
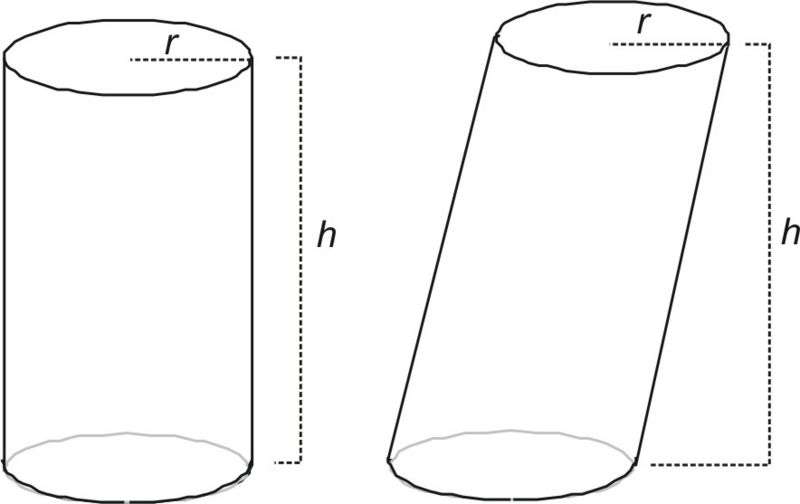
Если образующая линия перпендикулярна основаниям фигуры, тогда говорят о прямом цилиндре. В противном случае цилиндр будет наклонным. Если соединить центральные точки двух оснований, то полученная прямая называется осью фигуры. Приведенный рисунок демонстрирует разницу между прямым и наклонным цилиндрами.
Видно, что для прямой фигуры длина образующего отрезка совпадает со значением высоты h. Для наклонного цилиндра высота, то есть расстояние между основаниями, всегда меньше длины образующей линии.
Далее охарактеризуем осевые сечения обоих типов цилиндров. При этом будем рассматривать фигуры, основаниями которых является круг.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Осевое сечение прямого цилиндра
Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.
В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.
Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.
Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:
Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.
Видео:Тема 4. Цилиндр. Осевое сечение цилиндра. Развертка боковой поверхности цилиндра. Площадь боковойСкачать

Осевое сечение наклонного цилиндра
Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны — это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же — длина образующего отрезка. Обозначим ее b.
Читайте также: Дэу нексия замена задних тормозных цилиндров
Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:
Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:
Здесь l1 и l2 — длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.
Видео:Видеоурок по математике "Цилиндр"Скачать

Задача с прямым цилиндром
Покажем, как использовать полученные знания для решения следующей задачи. Пусть дан круглый прямой цилиндр. Известно, что осевое сечение цилиндра — квадрат. Чему равна площадь этого сечения, если площадь поверхности всей фигуры составляет 100 см2?
Для вычисления искомой площади необходимо найти либо радиус, либо диаметр основания цилиндра. Для этого воспользуемся формулой для общей площади Sf фигуры:
Поскольку сечение осевое представляет собой квадрат, то это означает, что радиус r основания в два раза меньше высоты h. Учитывая это, можно переписать равенство выше в виде:
Теперь можно выразить радиус r, имеем:
Поскольку сторона квадратного сечения равна диаметру основания фигуры, то для вычисления его площади S будет справедлива следующая формула:
Мы видим, что искомая площадь однозначно определяется площадью поверхности цилиндра. Подставляя данные в равенство, приходим к ответу: S = 21,23 см2.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
Цилиндр — это симметричная пространственная фигура, свойства которой рассматривают в старших классах школы в курсе стереометрии. Для его описания используют такие линейные характеристики, как высота и радиус основания. В данной статье рассмотрим вопросы касательно того, что такое осевое сечение цилиндра, и как рассчитать его параметры через основные линейные характеристики фигуры.
Видео:№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположныеСкачать

Геометрическая фигура
Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.
На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.
Здесь отрезок длиной h является его образующей и высотой.
Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.
Видео:№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Прямой и наклонный цилиндры
Перед тем как переходить к рассмотрению осевого сечения цилиндров, расскажем, какие типы этих фигур бывают.
Если образующая линия перпендикулярна основаниям фигуры, тогда говорят о прямом цилиндре. В противном случае цилиндр будет наклонным. Если соединить центральные точки двух оснований, то полученная прямая называется осью фигуры. Приведенный рисунок демонстрирует разницу между прямым и наклонным цилиндрами.
Читайте также: Замена заднего тормозного цилиндра портер 1
Видно, что для прямой фигуры длина образующего отрезка совпадает со значением высоты h. Для наклонного цилиндра высота, то есть расстояние между основаниями, всегда меньше длины образующей линии.
Далее охарактеризуем осевые сечения обоих типов цилиндров. При этом будем рассматривать фигуры, основаниями которых является круг.
Видео:Задание №757 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

Осевое сечение прямого цилиндра
Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.
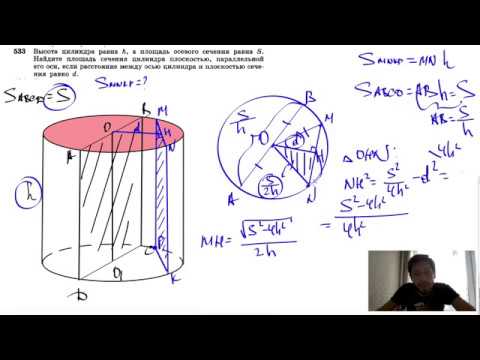
В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.
Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.
Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:
Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.
Видео:9 класс, 41 урок, ЦилиндрСкачать

Осевое сечение наклонного цилиндра
Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны — это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же — длина образующего отрезка. Обозначим ее b.
Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:
Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:
Здесь l1 и l2 — длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.
Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Задача с прямым цилиндром
Покажем, как использовать полученные знания для решения следующей задачи. Пусть дан круглый прямой цилиндр. Известно, что осевое сечение цилиндра — квадрат. Чему равна площадь этого сечения, если площадь поверхности всей фигуры составляет 100 см2?
Для вычисления искомой площади необходимо найти либо радиус, либо диаметр основания цилиндра. Для этого воспользуемся формулой для общей площади Sf фигуры:
Поскольку сечение осевое представляет собой квадрат, то это означает, что радиус r основания в два раза меньше высоты h. Учитывая это, можно переписать равенство выше в виде:
Теперь можно выразить радиус r, имеем:
Поскольку сторона квадратного сечения равна диаметру основания фигуры, то для вычисления его площади S будет справедлива следующая формула:
Мы видим, что искомая площадь однозначно определяется площадью поверхности цилиндра. Подставляя данные в равенство, приходим к ответу: S = 21,23 см2.
Читайте также: Замена сальника рабочего цилиндра сцепления
Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Что такое цилиндр: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Видео:11 класс, 32 урок, Объем цилиндраСкачать

Определение цилиндра
Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Видео:Объем цилиндра.Скачать

Основные элементы цилиндра
- Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O1 и O2.
- R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
- O1O2 – ось симметрии цилиндра, одновременно является его высотой (h).
- l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.
- длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
- ширина равна высоте/образующей цилиндра.
Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.
Видео:ЦИЛИНДР геометрия егэ по математике профильный уровень ЯщенкоСкачать

Диаметр и диагональ цилиндра
Видео:Цилиндр | МатематикаСкачать

Свойства
Зная диаметр цилиндра, можно вычислить радиус цилиндра и периметр окружности цилиндра, которая представляет собой его основание. Радиус будет равен одной второй диаметра, а периметр окружности – произведению диаметра на число π. r=D/2 P=πD
Первое, что можно вычислить через диаметр и диагональ цилиндра – это его высота. Так как высота непосредственно связана со всеми остальными параметрами цилиндра, такими как площадь, объем и прочие, то она является необходимым звеном для геометрического калькулятора цилиндра. (рис.25.1) h=√(d^2-D^2 )
Площадь боковой поверхности цилиндра равна произведению высоты на длину окружности в основании цилиндра, таким образом, раскрывая эту формулу, получаем, что площадь боковой поверхности равна произведению числа π и диаметра на квадратный корень из разности квадратов диагонали и диаметра. S_(б.п.)=hP=πD√(d^2-D^2 )
Площадь полной поверхности цилиндра представлена площадью боковой поверхности в сумме с площадью двух оснований в виде окружностей. S_(п.п.)=S_(б.п.)+2S_(осн.)=πD(√(d^2-D^2 )+D)
Чтобы найти объем цилиндра через диаметр и диагональ нужно представить высоту цилиндра в виде квадратного корня разности из квадратов диагонали и диаметра, а затем умножить это на площадь основания, состоящую из числа π и четверти квадрата диаметра. V=(πD^2 h)/4=(πD^2 √(d^2-D^2 ))/4
Чтобы в цилиндр можно было вписать сферу, нужно чтобы диаметр цилиндра был равен его высоте, тогда сфера будет соприкасаться со всеми гранями цилиндра и ее радиус будет равен радиусу цилиндра, то есть половине его диаметра. (рис. 25.2) r_1=r=D/2
Чтобы вокруг цилиндра можно было описать сферу, нужно точно так же чтобы диаметр цилиндра совпадал с высотой, и радиус описанной сферы будет равен половине диагонали цилиндра. R=d/2
🔥 Видео
Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

ЦилиндрСкачать

№533. Высота цилиндра равна h, а площадь осевого сечения равна 5. Найдите площадь сеченияСкачать