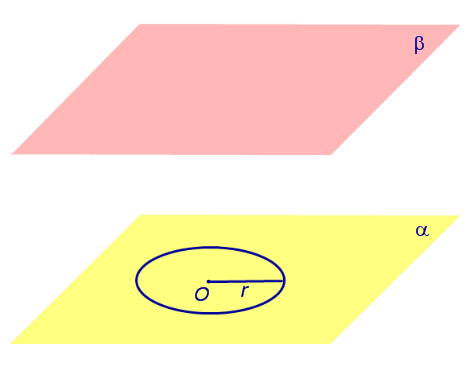
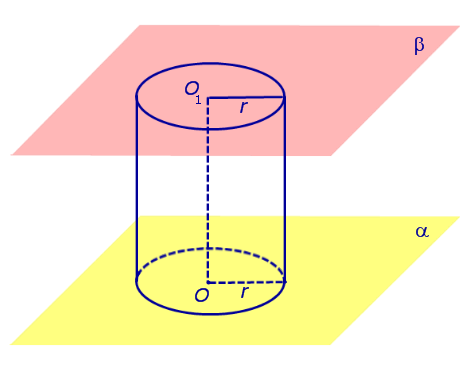
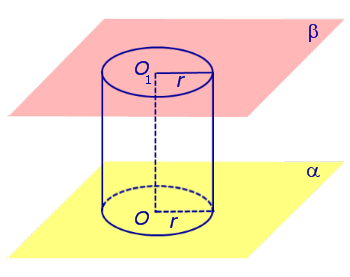
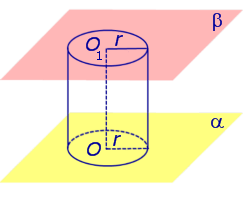
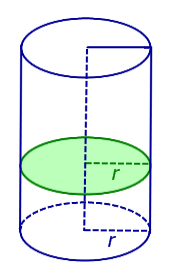
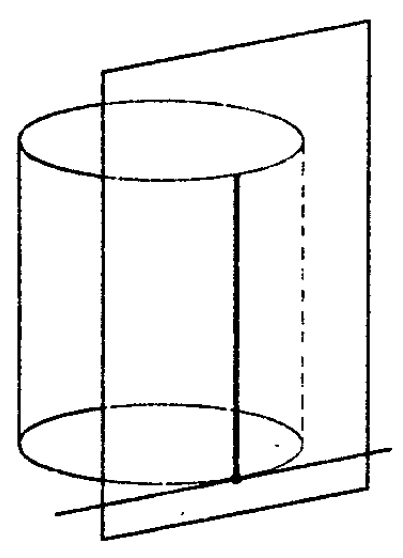
Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O1 которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).
Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .
Совокупность всех образующих цилиндра называют цилиндрической поверхностью .
Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .
Отрезок OO1 называют осью цилиндра .
Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .
Круги с центрами O и O1 на плоскостях α и β , называют основаниями цилиндра .
Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .
Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.
Замечание 3. Прямая OO1 является осью симметрии цилиндра, а середина отрезка OO1 является центром симметрии цилиндра.
- Сечения цилиндра
- Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра
- Что такое цилиндр: определение, элементы, виды, варианты сечения
- Определение цилиндра
- Основные элементы цилиндра
- wiki.eduVdom.com
- Инструменты пользователя
- Инструменты сайта
- Боковая панель
- Цилиндр
- Цилиндр
- Определение
- Объем цилиндра
- Доказательство:
- Площадь боковой поверхности цилиндра
- 📹 Видео
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Сечения цилиндра
Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
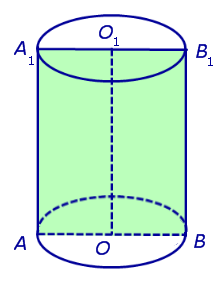
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).
На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA1B1B .
Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .
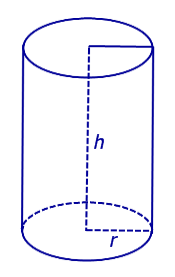
Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).
Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .
Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».
Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра
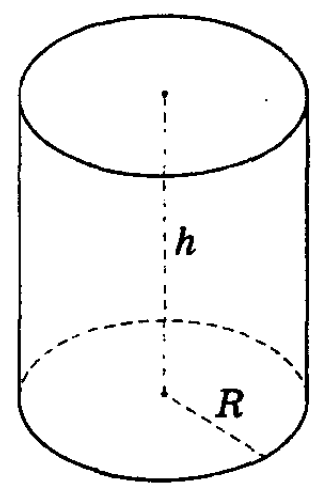
Для цилиндра с радиусом r и высотой h (рис. 5)
Читайте также: Как найти объем цилиндра если в него вписан правильный треугольник
введем следующие обозначения
| V | объем цилиндра |
| Sбок | площадь боковой поверхности цилиндра |
| Sполн | площадь полной поверхности цилиндра |
| Sосн | площадь основания цилиндра |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:
при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
Видео:Видеоурок по математике "Цилиндр"Скачать

Что такое цилиндр: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Видео:Геометрия 10 класс ЦилиндрСкачать

Определение цилиндра
Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.
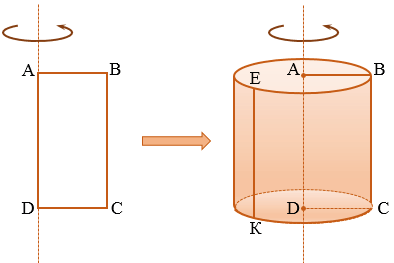
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Видео:9 класс, 41 урок, ЦилиндрСкачать

Основные элементы цилиндра
- Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O1 и O2.
- R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
- O1O2 – ось симметрии цилиндра, одновременно является его высотой (h).
- l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.
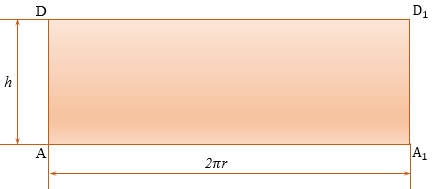
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.
- длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
- ширина равна высоте/образующей цилиндра.
Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.
Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

wiki.eduVdom.com
Инструменты пользователя
Инструменты сайта
Боковая панель
Стереометрия:
Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Цилиндр
Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.
Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.
Читайте также: Лабораторная работа по физике определить удельную теплоемкость металлического цилиндра
Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.
Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.
Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.
Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.
Круговой цилиндр — цилиндр, основания которого являются кругами.
Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.
Радиус цилиндра – радиус его основания.
Образующая цилиндра — образующая цилиндрической поверхности.
Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.
Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.
Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_ =2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.
Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_ =2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.
Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).
Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.
Видео:Объём цилиндраСкачать

Цилиндр
Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая ограничена кривой и крутится вокруг оси, лежащей в той же плоскости. К телам вращения относятся цилиндр, конус и шар.
Цилиндр — это объемное тело, которое получается при вращении прямоугольника вокруг одной из его сторон.
Читайте также: Снимаем главный тормозной цилиндр ваз 2114
Возьмем прямоугольник АВСD. Будем вращать этот прямоугольник против часовой стрелки вокруг стороны АD.
Прямая АD — ось цилиндра.
Отрезок АD — высота цилиндра.
Основания цилиндра — два равных круга образованных при вращении сторон АВ и DC (круги равные, т.к. стороны АВ и DC равны как противоположные стороны прямоугольника).
Радиус цилиндра — радиус оснований цилиндра.
Цилиндрическая поверхность (или боковая поверхность цилиндра) — поверхность, образованная при вращении стороны ВС и состоящая из отрезков, параллельных оси цилиндра (АD).
Образующие цилиндра — отрезки, из которых составлена боковая поверхность цилиндра (на рисунке выше указаны образующие ВС и ЕК).
Определение
Объем цилиндра
Доказательство:
Дано: цилиндр с площадью основания S, высотой h и объемом V.
Доказать: V = Sh.
Доказательство:
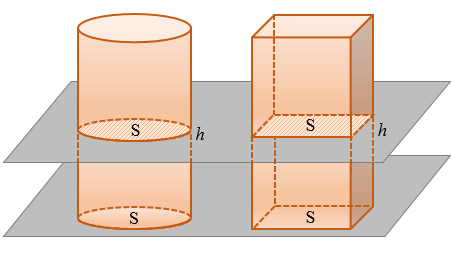
Воспользуемся принципом Кавальери. Рассмотрим цилиндр и призму с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости.
Любая секущая плоскость, параллельная плоскости, на которой стоят цилиндр и призма, дает в качестве сечения цилиндра круг площади S, а в качестве сечения призмы — многоугольник площади S. Значит, объем цилиндра равен объему призмы. Но объем призмы равен Sh. Поэтому и объем цилиндра равен Sh, т.е. V = Sh. Что и требовалось доказать.
Площадь боковой поверхности цилиндра
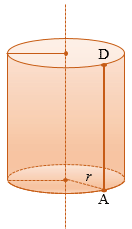
Рассмотрим цилиндр с радиусом r и высотой h.
Представим, что его боковую поверхность разрезали по одной из его образующих АD и развернули так, что получился прямоугольник АDА1D1, стороны АD и А1D1 которого являются двумя краями разреза боковой поверхности цилиндра. Этот прямоугольник называется разверткой боковой поверхности цилиндра.
Сторона АА1 прямоугольника АDА1D1 равна длине окружности основания, а сторона АD равна высоте цилиндра, т.е. АА1 = 2 r, АВ = h. Площадь прямоугольника равна произведению его смежных сторон, значит, площадь прямоугольника АDА1D1 равна 2 rh.
Площадь Sбок боковой поверхности цилиндра равна площади ее развертки, т.е. Sбок = 2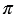 rh. rh. |
Поделись с друзьями в социальных сетях:
📹 Видео
ЦИЛИНДР КОНУС И ШАР 9 класс Атанасян геометрияСкачать

11 класс, 14 урок, Понятие цилиндраСкачать

59. Понятие цилиндраСкачать

Конус. 11 класс.Скачать

ЦИЛИНДР геометрия егэ по математике профильный уровень ЯщенкоСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

ЦИЛИНДР. КОНУС. ШАР.Скачать

ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

Геометрия 9 класс (Урок№34 - Тела и поверхности вращения.)Скачать

11 класс. Геометрия. Объем цилиндраСкачать

Объем цилиндра. Практическая часть. 11 класс.Скачать

ЦИЛИНДР | 9 класс геометрия Атанасян | задачи 1215 1217Скачать