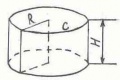
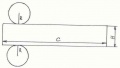
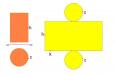
Поверхность цилиндра состоит из двух равных кругов радиуса R и прямоугольника, ширина которого равна высоте цилиндра, длина вычисляется по формуле С=2пR , где п=3,14. Изображение цилиндра и его развертка на рисунках:
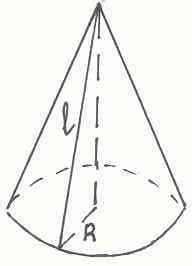
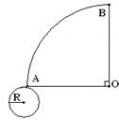
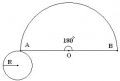
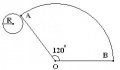
Поверхность конуса состоит круга радиуса R и сегмента круга радиуса OA. Дуга АВ=2пR. Изображение конуса и его разверток показаны на рисунках:
а) Когда угол прямой имеем четверть круга. Чтобы дуга АВ=2пR, надо чтобы АО=4R
б) Когда угол развернутый имеем половину круга. Чтобы дуга АВ=2пR, надо чтобы АО=2R
в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AB=2пR, надо чтобы АО=3R
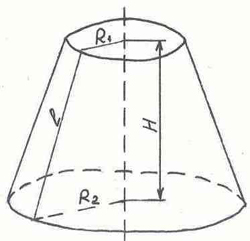
Развертка «Усеченный конус»
Поверхность усеченного конуса состоит двух кругов радиуса R1 , R2 и сегмента круга радиуса OA. Дуга AB=2пR. Изображение усеченного конуса и его разверток показаны на рисунках:
а) Когда угол прямой имеем четверть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=4R1, В1О=4R2
б) Когда угол развернутый имеем половину круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=2R1, В1О=2R2
в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=3R1, В1О=3R2
- Круглый прямой цилиндр, развертка и формула для ее площади
- Цилиндр как фигура геометрии
- Круглый прямой цилиндр
- Развертка круглого прямого цилиндра
- Площадь развертки цилиндра
- Задача на нахождение радиуса фигуры
- Калькулятор развертки усеченного плоскостью цилиндра онлайн
- Обозначения
- Введите радиус или диаметр *:
- Введите высоты * и (или) угол:
- Округление:
- Построение развёртки:
- Графики
- Формулы
- Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
- Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
- Развертка прямого кругового цилиндра.
- Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
- Развертка усеченного цилиндра.
- 🎥 Видео
Видео:Цилиндр - расчёт площади, объёма.Скачать

Круглый прямой цилиндр, развертка и формула для ее площади
Цилиндр — это одна из пространственных фигур, которая является объектом изучения стереометрии. Важная характеристика любой фигуры — это площадь ее поверхности. В данной статье рассмотрим, что собой представляет развертка цилиндра, а также покажем, как вычислить ее площадь.
Видео:Построение развертки цилиндра. Урок 37.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Цилиндр как фигура геометрии
Предположим, что у нас имеется некоторая плавная кривая. Это может быть круг, эллипс, парабола и так далее. Возьмем отрезок произвольной длины, который не лежит в плоскости кривой, и опишем с помощью него поверхность, следуя направлению кривой и транслируя отрезок параллельно самому себе. Полученная поверхность называется цилиндрической или просто цилиндром. Отмеченная кривая называется директрисой (направляющей), а отрезок — генератрисой (образующей).
Если к цилиндрической поверхности добавить еще две плоские одинаковые фигуры, ограничивающие эту поверхность с торцов, то полученное тело также называется цилиндром. Оно состоит из двух равных оснований и цилиндрической поверхности.
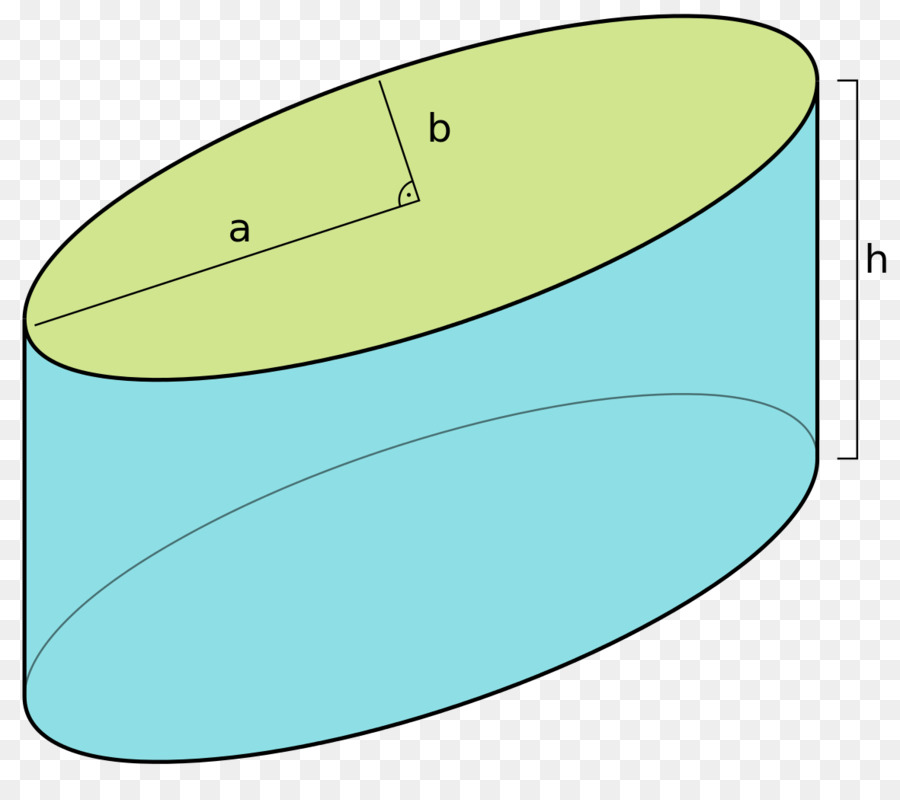
Для наглядного представления описанной фигуры ниже приведен рисунок. На нем изображен эллиптический цилиндр, имеющий полуоси a и b и высоту h (дистанция между основаниями).
Видео:Простой расчёт развёртки конусаСкачать

Круглый прямой цилиндр
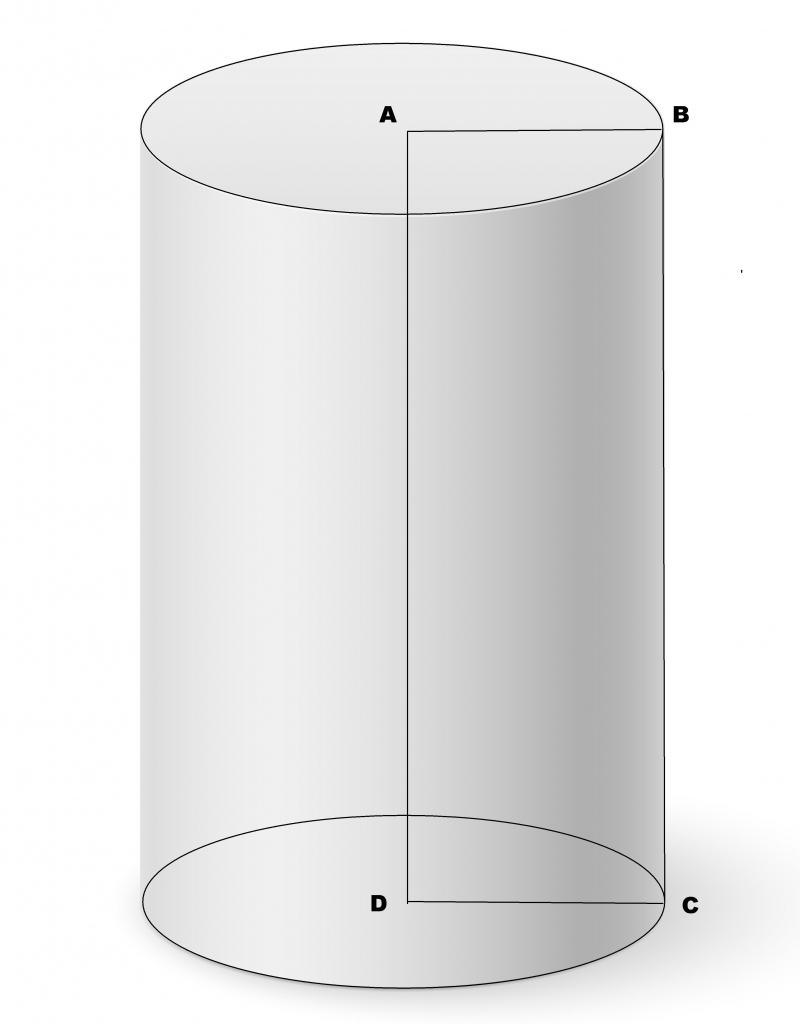
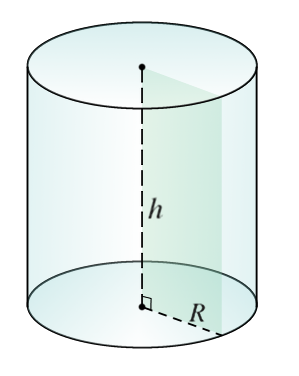
Пусть директрисой будет окружность некоторого радиуса. Тогда образованная генератрисой фигура будет называться круглым цилиндром. Тем не менее генератриса относительно плоскости, ограниченной директрисой, может быть направлена произвольным образом. Поэтому в общем случае говорят о наклонном круглом цилиндре. Если же генератриса будет перпендикулярна плоскостям основания, то цилиндр называется прямым. Он показан на рисунке ниже.
Читайте также: Мотоциклист едет по внутренней поверхности вертикального цилиндра радиусом
Здесь AB = DC — радиус цилиндра, AD = BC = h — высота фигуры. Для прямого цилиндра высота всегда равна длине образующей. Отрезок AD обозначает ось цилиндра — прямая, соединяющая две центральные точки оснований. От оси цилиндра все точки боковой поверхности лежат на одном расстоянии, равном радиусу фигуры.
Далее в статье будем рассматривать развертку поверхности цилиндра, круглого и прямого.
Видео:Компас-3D v16. Параметрическое определение длины развертки гнутой трубы.Скачать

Развертка круглого прямого цилиндра
Когда говорят о развертке цилиндра, то подразумевают общую площадь его поверхности, представленную плоскими фигурами. Круглый прямой цилиндр образован двумя кругами, имеющими одинаковые радиусы, и одной боковой поверхностью, которая эти круги соединяет друг с другом.
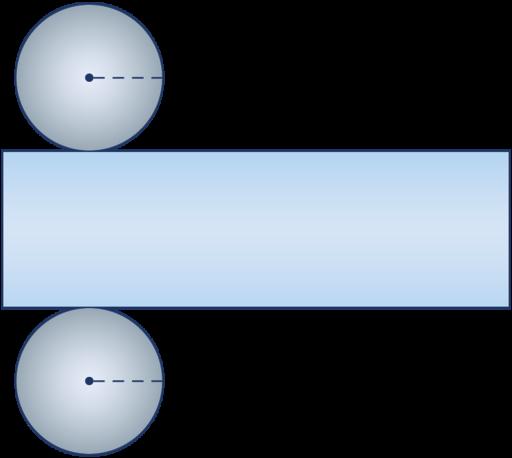
На рисунке показан бумажный цилиндр. Как осуществляется построение развертки цилиндра? Возьмем воображаемые ножницы и отрежем одно основание вдоль окружности. Затем проделаем аналогичные действия со вторым основанием. Боковую поверхность разрежем вдоль генератрисы, то есть параллельно оси фигуры, и развернем ее. Таким образом, мы получили развертку, которая показана на рисунке ниже.
Очевидно, что она состоит из двух одинаковых кругов. Что касается цилиндрической поверхности, то в разрезанном виде она представлена прямоугольником. Развертку удобно использовать при определении площади поверхности рассматриваемой фигуры.
Видео:Виды разверток по металлу. Цилиндрическая, коническая, разжимные и раздвижные разверткиСкачать

Площадь развертки цилиндра
Выше мы показали, как можно получить развертку фигуры. Чтобы рассчитать ее площадь, необходимо сложить площади для всех ее частей, то есть для двух круглых оснований и одного прямоугольника.
Обозначим радиус основания буквой r, а высоту фигуры — буквой h. Площадь одного основания равна площади круга, то есть:
Здесь pi — число Пи, приблизительно равное 3,14.
Чтобы вычислить площадь прямоугольника, представляющего боковую поверхность фигуры в развернутом виде, необходимо знать две его стороны. Одна из них равна высоте h. Вторая, как можно догадаться, соответствует длине директрисы, то есть длине окружности. Обозначим ее l. Тогда можно записать следующие равенства:
Здесь Sb — площадь прямоугольника, равная площади цилиндрической поверхности.
Учитывая, что фигура имеет два основания, складываем рассчитанные величины, получаем общую площадь развертки цилиндра:
Площадь S фигуры однозначно определяется через ее радиус и высоту.
Покажем, как использовать это равенство для решения геометрической задачи.
Видео:Построение развёртки усечённого цилиндра.Скачать

Задача на нахождение радиуса фигуры
Известно, что общая поверхность круглого прямого цилиндра составляет 60 см 2 . Чему равен радиус основания цилиндра, если его высота равна 7 см, а фигура имеет лишь одно основание.
Описанный в условии задачи цилиндр представляет собой бочку без крышки, поэтому площадь его поверхности образована не двумя, а одним основанием.
Если учесть названный факт, тогда формула для площади фигуры запишется в следующем виде:
Читайте также: Ремкомплект главного цилиндра сцепления уаз 3909
Подставим все известные из условия величины в это равенство, получим:
Мы получили классическое полное квадратное уравнение. Его решение даст искомое значение радиуса r. Решаем через дискриминант:
При решении уравнения отрицательный корень был отброшен, в виду его нефизического значения.
Таким образом, параметры открытого цилиндра из условия задачи составляют 7 см в высоту и 2,5 см в диаметре.
Видео:Развертка по металлу. Конструкция и назначение. Припуск под развертывание отверстийСкачать

Калькулятор развертки усеченного плоскостью цилиндра онлайн
Видео:Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать
Обозначения
- R — радиус основания цилиндра;
- D — диаметр основания цилиндра;
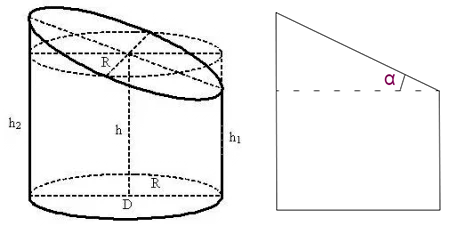
- h — средняя высота усечённого цилиндра;
- h1 — наименьшая высота усечённого цилиндра;
- h2 — наибольшая высота усечённого цилиндра;
- α — угол сечения, град.
- X1 .. n — координаты для построения развёртки по оси X;
- Y1 .. n — координаты для построения развёртки по оси Y;
Числовые значения в таблице заполняются числом (5; 5.16; -3.12), либо математическим выражением (5/7; (1-5)*2.13)
Введите радиус или диаметр *:
Введите высоты * и (или) угол:
Без макс. и мин. высоты можно посчитать только площади боковой поверхности и основания и объём
Или введите одну из высот и угол сечения (рис.)
Округление:
Построение развёртки:
Видео:Поиск нейтрального слоя в листовом металлеСкачать

Графики
Чертится развертка усеченного плоскостью цилиндра, как показано на рисунке:
Видео:Развертка цилиндраСкачать

Формулы
Формула для вычисления значений Y:
Yi = D * tg(α) * sin (i * (180 / n)) , здесь: i — номер точки, α — угол сечения, n — количество точек развертки, D — диаметр цилиндра;
Формула для вычисления значений X:
Xi = ((π * R 2 ) / n) * i , здесь: i — номер точки, α — угол сечения, n — количество точек развертки, R — радиус цилиндра, π — число Пи (прим. 3.14);
Видео:Видеоурок по математике "Цилиндр"Скачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Видео:Расчет развертки листовой детали под разными угламиСкачать
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Развертка прямого кругового цилиндра.
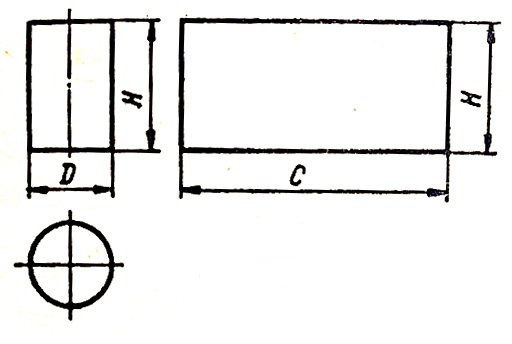
Цилиндр диаметром D и высотой H показан на рис. 1. Развертка представляет собой прямоугольник длиной с = πD и высотой Н.
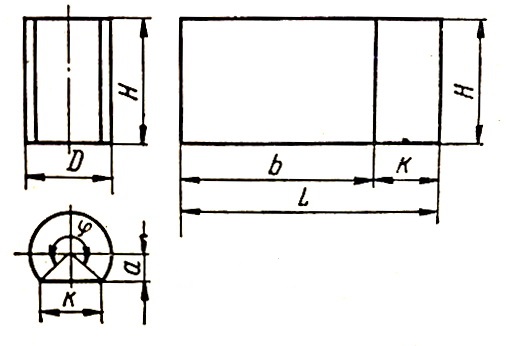
Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2) 2 – a 2 ) = 2a tg (ᵠ/2).
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
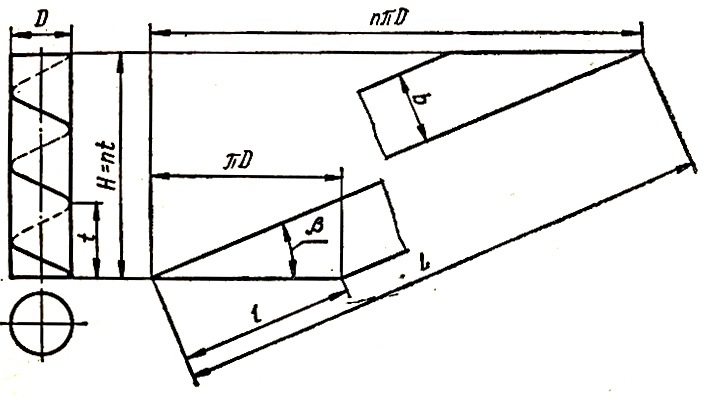
Цилиндр показан на рис. 3. При определении развертки можно использовать следующие зависимости:
n — число полных витков на общей длине цилиндра H, Н = nt;
Развертка усеченного цилиндра.
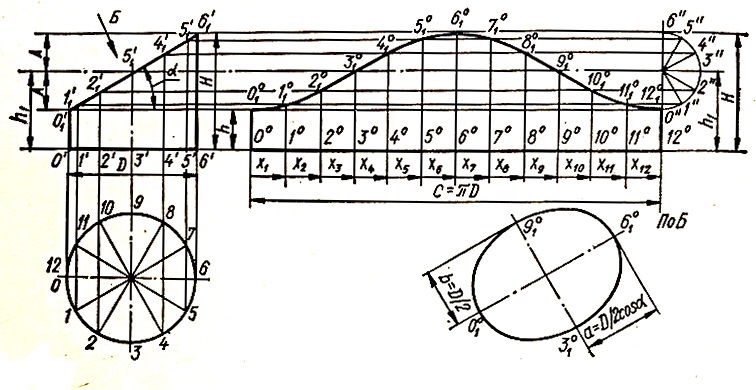
Для получения развертки горизонтальная проекция цилиндра делится на равные части и точки деления нумеруются (в данном случае от 0 до 12). Из точек деления проводятся вертикали до пересечения верхнего основания в точках 0′1, 1′1…, 6′1. На продолжении прямой 0’6′ откладывается отрезок длиной с = πD, который делится на принятое число равных частей. Из точек деления 00, 10, …, 60 строятся перпендикуляры до их пересечения с соответствующими горизонтальными линиями в точках 0 0 1, 1 0 1, …, 6 0 1. Полученные точки соединяются плавной кривой. Ввиду симметричности остальные точки кривой находит аналогичным путем.
Линию развертки можно определить и таким способом. На расстоянии h1 = (h + H)/2 от линии 0 0 12 0 проводится параллельная прямая. Из центра S, лежащего на прямой, описывается полуокружность радиусом А. Полуокружность делится на равные части, число которых равно половине точек деления развертки (в данном случае на шесть). Через точки деления 0ꞋꞋ, 1ꞋꞋ, …, 6ꞋꞋ проводятся горизонтальные прямые до пересечения вертикалей, проходящих через 0 0 , 1 0 , … , 12 0 . Полученные точки 0 0 1, 1 0 1, …, 12 0 1 соединяются плавной кривой.
Читайте также: Как измерить линейкой высоту цилиндра
Верхнее основание цилиндра представляет собой эллипс с полуосями a = D/2 cos α = 0′13′1 и b = D/2.
При аналитическом определении координат точек кривой развертки цилиндра, усеченного плоскостью под углом α (рис. 5), могут быть использованы следующие зависимости:
xk = kx1 = πD/2 kε/180°; yk = D/2 tg α sin kε = A sin kε = A sin ᵠi,
где х1 = πD/ (2n) = πD/2 ε/180° — длина дуги окружности основания цилиндра, разделенная на 2n равных частей; ε = 360°/2n — центральный угол, соответствующий одному делению; k — порядковый номер точки; A = (H — h)/2 = (D/2) tg α — амплитуда синусоиды; ᵠi= kε.
Значения sin kε для наиболее часто употребляемых значений 2n приведены в табл. 1.
Таблица 1. Значения sin kε и sin 2 kε
| 2n | sin kε | sin 2 kε | 2n | sin kε | sin 2 kε | ||||||
| 8 | 16 | 32 | 64 | 12 | 24 | 48 | 96 | ||||
| — | — | — | 1 | 0,09802 | 0,00961 | — | — | — | 1 | 0,06540 | 0,00428 |
| — | — | 1 | 2 | 0,19509 | 0,03806 | — | — | 1 | 2 | 0,13053 | 0,01704 |
| — | — | — | 3 | 0,29028 | 0,08426 | — | — | — | 3 | 0,19509 | 0,03806 |
| — | 1 | 2 | 4 | 0,38268 | 0,14645 | — | 1 | 2 | 4 | 0,25882 | 0,06699 |
| — | — | — | 5 | 0,47139 | 0,22221 | — | — | — | 5 | 0,32144 | 0,10332 |
| — | — | 3 | 6 | 0,55557 | 0,30866 | — | — | 3 | 6 | 0,38268 | 0,14645 |
| — | — | — | 7 | 0,63439 | 0,40245 | — | — | — | 7 | 0,44229 | 0,19562 |
| 1 | 2 | 4 | 8 | 0,70711 | 0,50000 | 1 | 2 | 4 | 8 | 0,50000 | 0,25000 |
| — | — | — | 9 | 0,77301 | 0,59754 | — | — | — | 9 | 0,55557 | 0,30866 |
| — | — | 5 | 10 | 0,83147 | 0,69134 | — | — | 5 | 10 | 0,60876 | 0,37059 |
| — | — | — | 11 | 0,88192 | 0,77778 | — | — | — | 11 | 0,65935 | 0,43474 |
| — | 3 | 6 | 12 | 0,92388 | 0,85355 | — | 3 | 6 | 12 | 0,70711 | 0,50000 |
| — | — | — | 13 | 0,95694 | 0,91573 | — | — | — | 13 | 0,75184 | 0,56526 |
| — | — | 7 | 14 | 0,98079 | 0,96194 | — | — | 7 | 14 | 0,79335 | 0,62941 |
| — | — | — | 15 | 0,99518 | 0,99039 | — | — | — | 15 | 0,83147 | 0,69134 |
| 2 | 4 | 8 | 16 | 1,00000 | 1,00000 | 2 | 4 | 8 | 16 | 0,86617 | 0,75000 |
| — | — | — | 17 | 0,89687 | 0,80438 | ||||||
| — | — | 9 | 18 | 0,92388 | 0,85355 | ||||||
| — | — | — | 19 | 0,94693 | 0,89668 | ||||||
| — | 5 | 10 | 20 | 0,96600 | 0,93301 | ||||||
| — | — | — | 21 | 0,98079 | 0,96194 | ||||||
| — | — | 11 | 22 | 0,99144 | 0,98296 | ||||||
| — | — | — | 23 | 0,99786 | 0,99572 | ||||||
| 3 | 6 | 12 | 24 | 1,00000 | 1,00000 | ||||||
Примечание: Значения sin kε и sin 2 kε даны для одной четверти окружности. В остальных четвертях они повторяются.
Ввиду симметричности синусоиды достаточно определить координаты точек одной четверти окружности, например от у0 до у3. Остальные координаты имеют соответственно равные значения. Например: у4 — у2, …, у11 = — у1 и т. д.
🎥 Видео
Расчет развертки усеченного цилиндра в Компас 3Д. Чертеж развертки усеченного цилиндра.Скачать

+Как найти длину окружностиСкачать

36. Построение развертки цилиндра с линией пересеченияСкачать

СТРОГО ПО ЦЕНТРУ !!! БЕЗ СТАНКА И ТОКАРЯ, как просверлить отверстие в болтеСкачать

Уроки Компас 3D.Развертка цилиндраСкачать

Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Длина развёрткиСкачать