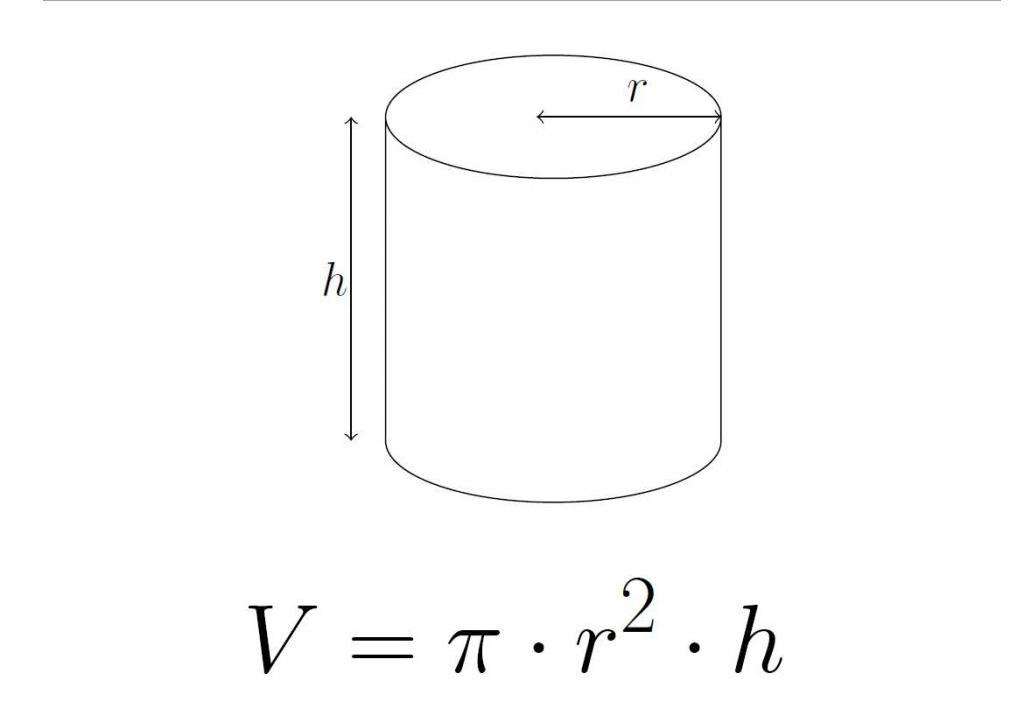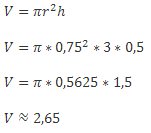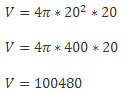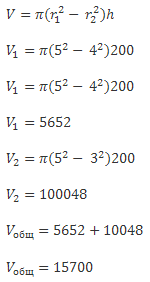Как определить объем цилиндра физика 7 класс

Объем является физической величиной, которая присуща телу с ненулевыми размерами вдоль каждого из трех направлений пространства (все реальные объекты). В статье в качестве примера формулы объема рассматривается соответствующее выражение для цилиндра.

Видео:Цена деления, погрешность и объем жидкости в мензуркеСкачать

Объем тел

Эта физическая величина показывает, какую часть пространства занимает то или иное тело. Например, объем Солнца намного больше этой величины для нашей планеты. Это означает, что принадлежащее Солнцу пространство, в котором находится вещество этой звезды (плазма), превышает земную пространственную область.

Объем изменяется в кубических единицах длины, в СИ это метры в кубе (м3). На практике объемы жидких тел измеряют в литрах. Маленькие объемы могут выражать в кубических сантиметрах, миллилитрах и других единицах.

Для вычисления объема формула будет зависеть от геометрических особенностей рассматриваемого объекта. Например, для куба это тройное произведение длины его ребер. Ниже рассмотрим фигуру цилиндр и ответим на вопрос о том, как найти объем его.

Видео:Урок 28 (осн). Вычисление массы и объема тела по плотностиСкачать

Понятие о цилиндре

Фигура, о которой пойдет речь, является достаточно непростой. Согласно геометрическому определению, она представляет собой поверхность, образованную путем параллельного перемещения прямой (генератрисы) вдоль некоторой кривой (директрисы). Генератриса также называется образующей, а директриса — направляющей.

Если директриса — это окружность, а генератриса перпендикулярна ей, тогда полученный цилиндр называют круглым и прямым. О нем и пойдет дальше речь.

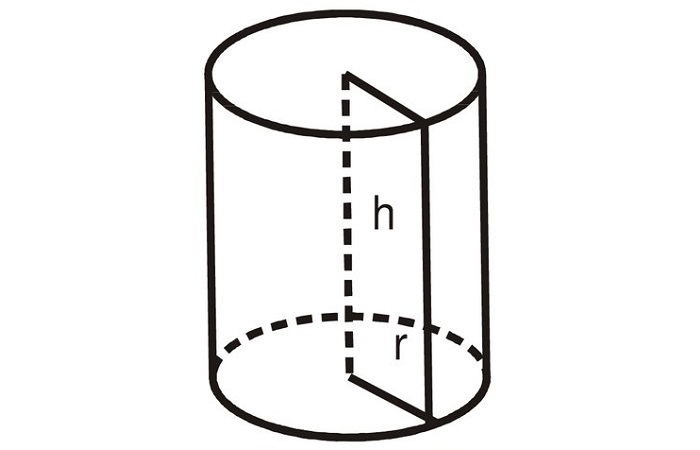
Цилиндр имеет два основания, которые параллельны друг другу и соединены цилиндрической поверхностью. Проходящая через центры двух оснований прямая называется осью круглого цилиндра. Все точки фигуры находятся на одинаковом расстоянии от этой прямой, которое равно радиусу основания.

Круглый прямой цилиндр однозначно определяется двумя параметрами: радиусом основания (R) и расстоянием между основаниями — высота H.

Видео:Определение объёма телаСкачать

Формула объема цилиндра

Для расчета области пространства, которую занимает цилиндр, достаточно знать его высоту H и радиус основания R. Искомое равенство в этом случае имеет вид:

Понять эту формулу объема просто: поскольку высота перпендикулярна основаниям, то если ее умножить на площадь одного из них, получается нужная величина V.

Видео:Определение показаний прибораСкачать

Вычисление объема бочки

Для примера решим такую задачу: определим, сколько воды поместится в бочку, имеющую диаметр дна 50 см и высоту 1 метр.

Радиус бочки равен R=D/2=50/2=25 см. Подставляем данные в формулу, получаем:

V = pi*R2*H = 3,1416*252*100 = 196350 см3

Поскольку 1 л = 1 дм3 = 1000 см3, то получаем:

V = 196350/1000 = 196,35 литра.

То есть в бочку можно налить почти 200 литров воды.

Видео:Объём цилиндраСкачать

Объем цилиндра — формулы и примеры расчетов

Как найти объем цилиндра? Любой грамотный человек обязан отличить радиус от диаметра, знать, что такое высота, помнить основные формулы геометрии и уметь рассчитать объем шара или куба.

Практическое использование геометрических формул в повседневной жизни очень высоко. Рассчитать объем в кубических метрах перевозимого груза транспортной компанией, пропускную способность трубы под домом и многое другое — во всех этих и подобных им случаях поможет геометрия.

Видео:Физика 7 класс (Урок№10 - Плотность и масса.)Скачать

Как найти объем цилиндра

При упоминании о цилиндре на ум приходит классический головной убор. Кроме него в окружении можно встретить много разновидностей этой фигуры.

Читайте также: Как выглядит передний тормозной цилиндр

В теории — это тело, которое ограничено цилиндрической поверхностью и пересекающими её параллельными плоскостями.

Рассчитать его объем возможно следующим образом:

Как видите, формула проста и прозрачна, и если обывателю нужно, как вариант, определить объем цистерны воды, можно смело ее использовать. Хотя, если возникают сомнения в правильности расчетов, для этой цели можно использовать калькулятор и определить объем онлайн.

Видео:Расчёт массы и объёма тела по его плотности. Физика 7 классСкачать

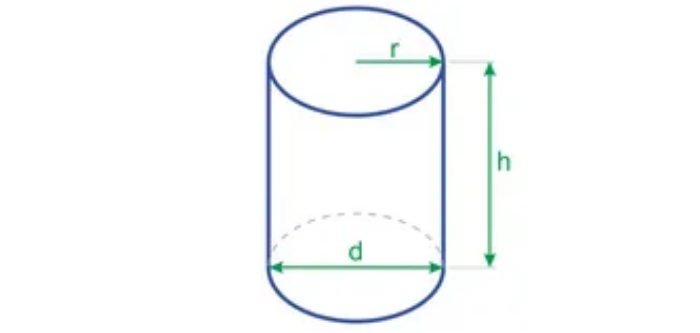
Формула объема цилиндра через диаметр

К сожалению, случается, что при расчете объема фигуры известны не все размеры. Так, например, может не быть данных о радиусе.

В данном случае, если знать диаметр или иметь возможность его измерить, можно воспользоваться следующей формулой:

Видео:Измерение объема с помощью мензуркиСкачать

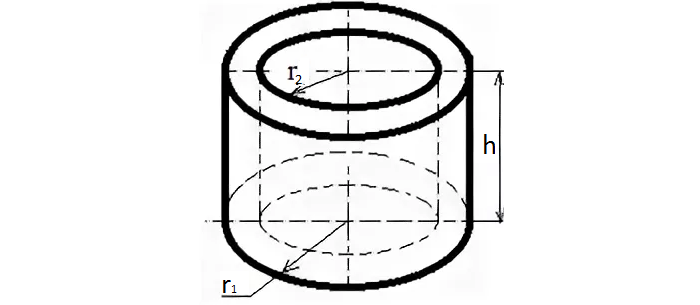
Объем полого цилиндра

Расчет полого цилиндра нужен, когда необходимо, например, рассчитать вес полой трубы. Ее масса равна произведению плотности материала и объема.

Видео:Объём телаСкачать

Примеры задач с решениями

Задача №1

Высота бочки с водой равна 3 метрам, радиус составляет 0,75 метра. Рассчитать в литрах, сколько нужно жидкости, чтобы заполнить емкость наполовину?

Задача №2

В цехе подготовили заготовку цилиндра. Диаметр основания равен высоте и составляет 20 см. Нужно найти объем заготовки.

Задача №3

На производстве нужно изготовить две трубы с двумя равными поверхностями. Внешний радиус первой трубы равен 5см, а внутренний 4 см, высота 200 см. Внутренний радиус второй равен 3 см.

Сколько понадобится материала для изготовления труб?

Видео:Как определить цену деления измерительного прибораСкачать

Как посчитать объем цилиндра

Видео:Физика 7 класс. 23 параграф. Расчёт массы и объёма тела по его плотностиСкачать

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ ( 1 /₂) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см 2 , то:

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см 2 , то:

V = 30 2 / _{4 ⋅ 3.14⋅ 5} = 900 /_62.8 = 14.33 см 3

Видео:Объем цилиндраСкачать

ГДЗ учебник по физике 7 класс Перышкин. №1 Определение цены деления измеррительного прибора. Номер №1

Цель работы:
Определить цену деления измерительного цилиндра (мензурки), научиться пользоваться им и определять с его помощью объём жидкости.
Приборы и материалы:
Измерительный цилиндр (мензурка), стакан с водой, небольшая колба и другие сосуды.
Указания к работе:
1 . Рассмотрите измерительный цилиндр (рис. 198 ), обратите внимание на его деления. Ответьте на следующие вопросы.
1 )Какой объём жидкости вмещает измерительный цилиндр, если жидкость налита:
а) до верхнего штриха;
б) до первого снизу штриха, обозначенного цифрой, отличной от нуля?
2 )Какой объём жидкости помещается:
а) между 2 −м и 3 −м штрихами, обозначенными цифрами;
б) между соседними (самыми близкими) штрихами мензурки?
2 . Как называется последняя вычисленная вами величина? Как определяют цену деления шкалы измерительного прибора?
Запомните: прежде чем проводить измерения физической величины с помощью измерительного прибора, определите цену деления его шкалы.
3 . Рассмотрите рисунок 7 учебника и определите цену деления изображённой на нём мензурки.
4 . Налейте в измерительный цилиндр воды, определите и запишите, чему равен объём налитой воды.
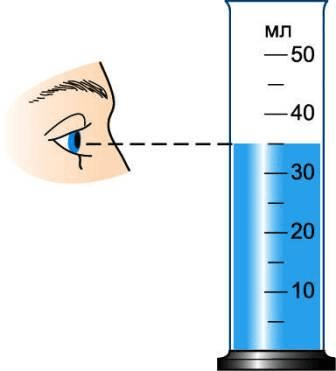
Примечание. Обратите внимание на правильное положение глаза при отсчёте объёма жидкости. Вода у стенок сосуда немного приподнимается, в средней же части сосуда поверхность жидкости почти плоская. Глаз следует направить на деление, совпадающее с плоской частью поверхности (рис. 198 ).
5 . Налейте полный стакан воды, потом осторожно перелейте воду в измерительный цилиндр. Определите и запишите с учётом погрешности, чему равен объём налитой воды. Вместимость стакана будет такой же.
6 . Таким же образом определите вместимость колбы, аптечных склянок и других сосудов, которые находятся на вашем столе.
7 . Результаты измерений запишите в таблицу 6 .

рис. 198 .

рис. 7 . Измерительный цилиндр.
Таблица 6 .

Решение

Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл.
1 .

Читайте также: Главный цилиндр сцепления газ 3110 сборка

1, а) Если жидкость налита до верхнего штриха, измерительный цилиндр вмещает 50 мл жидкости.
1, б) Если жидкость налита до первого снизу штриха, обозначенного цифрой, отличной от нуля, измерительный цилиндр вмещает 10 мл жидкости.
2, а) Между 2 − м и 3 −м штрихами, обозначенными цифрами, помещается 10 мл жидкости (например, возьмём штрихи 20 мл и 30 мл).
2, б) Между соседними (самыми близкими) штрихами мензурки (например, возьмём штрихи 30 и 35 ), помещается 5 мл жидкости.
2 . Последняя вычисленная нами величина является ценой деления измерительного цилиндра.
3 . На шкале цилиндра возьмём, к примеру, числа 50 и 60 . Количество маленьких штрихов между этими числами − 2 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл.
4 . Объём налитой воды равен 35 мл или 35 $см^ $ .
5 . Погрешность измерений равна половине цены деления шкалы измерительного прибора. Цена деления цилиндра − 5 мл, следовательно, погрешность измерения равна $\frac $ мл = 2,5 мл.
Объём налитой в полный стакан воды с учётом погрешности будет равен ( 200 ±∆ 2,5 ) мл ( $см^ $ ).
6 .
Таблица 6 .
| № опыта |Название сосуда| Объём жидкости $V_ , см^ $ |Вместимость сосуда, $V_ , см^ $ |
| −−− | −−− | −−− | −−− |
| 1 | стакан | 200 | 200 |
| 2 | колба | 50 | 50 |
| 3 | пузырёк | 30 | 30 |

Вывод. В ходе лабораторной работы мы определелили цену деления измерительного цилиндра, научились им пользоваться и научились с его помощью определять объём жидкости.

Видео:Измерение объема тел правильной и неправильной формы. Физика 7 классСкачать

Как определить объем цилиндра физика 7 класс

Формулы, используемые в задачах по физике на плотность, массу и объем.

🎬 Видео

Определение плотности твердого тела. 7 классСкачать

7 класс. Определение цены деления измерительного прибора и погрешности его измерения.Скачать

Плотность вещества | Физика 7 класс #15 | ИнфоурокСкачать

Определение цены деления измерительного цилиндра, определение с его помощью объема жидкости.Скачать

Видеоурок по математике "Цилиндр"Скачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Урок 6 (осн). Вычисление и измерение объемаСкачать