Как определить объем цилиндра погруженного в воду (5 видео)

Содержание

ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
Решение
Гидростатика. Сила Архимеда
🎥 Видео

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1

Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
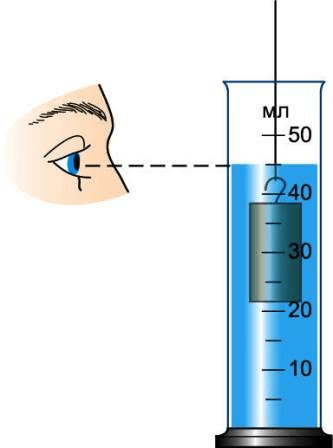
1 . Определите цену деления мензурки.
2 . Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
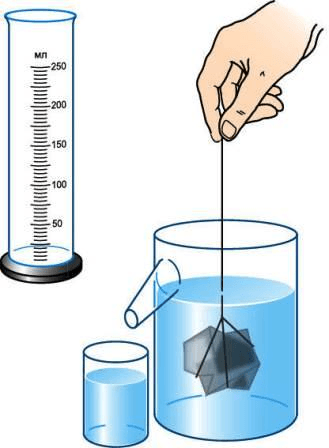
3 . Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201 ), и снова измерьте объём жидкости.
4 . Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5 . Результаты измерений запишите в таблицу 9 .
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202 ). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.

Таблица 9 .

рис. 201

рис. 202

Решение

Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
$V = V_ — V_ $ , где $V_ $ − объём воды и тела, $V_ $ − начальный объём воды в мензурке.

Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл.
В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70 $см^ $ .
Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
$V_ = 95 — 70 = 25 см^ $
$V_ = 85 — 65 = 20 см^ $
$V_ = 75 — 60 = 15 см^ $
Результаты измерений запишем в таблицу 9 .

Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.

Видео:Цилиндр - расчёт площади, объёма.Скачать

Гидростатика. Сила Архимеда

На погружённое в жидкость или газ тело действует выталкивающая сила, и равная весу среды, объём которой равен объёму тела.

Выталкивающая сила (сила Архимеда) равна

\[F_A=\rho_\text g V_\text \] где $\displaystyle V_\text $ — объём погружённой части тела, $\displaystyle \rho_\text $ — плотность жидкости.

Рассмотрим тело плотности $\rho$ и жидкость плотности $\rho_0$ . Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести $mg$ и архимедова сила $F_A$ . Если объём тела равен V, то

Имеются три возможности дальнейшего движения тела.

Сила тяжести больше архимедовой силы : $\displaystyle mg > F_A$ , или $\displaystyle \rho>\rho_0$ . В этом случае тело тонет.

Сила тяжести равна архимедовой силе : $\displaystyle mg = F_A$ , или $\displaystyle \rho=\rho_0$ . В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.

Сила тяжести меньше архимедовой силы : \(\displaystyle mg , или \(\displaystyle \rho . В этом случае тело всплывает, достигая поверхности жидкости.

Таким образом, условие плавания тела можно записать в виде неравенства $\displaystyle \rho\leq \rho_0$ .

Два жестко связанные друг с другом одинаковых бруска, имеющие толщину $h=5$ см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.)

Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
$\displaystyle\rho_1$ – плотность материала, из которого изготовлены бруски, а $\displaystyle V$ – объем двух брусков. Тогда масса этих брусков будет равна \[\displaystyle m=\rho_1V\] Сила, с которой льдинки действуют на воду, равна силе тяжести \[\displaystyle F=mg=\rho_1Vg\] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда \[F_\text =\rho g\frac 2,\] где $\displaystyle \rho$ – плотность воды, $\displaystyle \frac 2$ – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: \[\rho_1Vg=\rho g\frac 2,\] откуда $\displaystyle \rho_1=\dfrac 2,$ то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину \[\frac72h=3,5\cdot5\text =17,5 \text .\] Глубина увеличится на $\displaystyle 17,5 -5=12,5$ см.

Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна $\displaystyle \rho_\text =2700 \text /\text ^3. $ Какова длина ребра куба, если выталкивающая сила равна $\displaystyle F_\text =33,75\text ?$ (Ответ дайте в сантиметрах.)

Выталкивающая сила равна по определению \[F_\text =\rho_\text gV,\] где $\displaystyle \rho_\text $ – плотность жидкости, в которую погружен кубик, $\displaystyle V$ – объем погруженной части тела. Так как куб погружен целиком, то $\displaystyle V=a^3$ , получим: \[F_\text =\rho_\text ga^3\] Выразив из этой формулы сторону $\displaystyle a$ , получаем \[a=\sqrt[3] > g >>\] Подставив значения в формулу, получим: \[a=\sqrt[3] > / \cdot1000\text /\text ^3>>=0,15\text =15\text \]

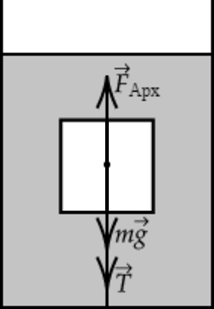
Однородный цилиндр, изготовленный из материала плотностью $\displaystyle \rho=600$ кг/м $^3$ , с радиусом основания $\displaystyle R=25$ см и высотой $\displaystyle H=20$ см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)

Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: \[\vec T+\vec F_\text +m\vec g=m\vec a,\] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: \[T- F_\text +mg=0, \quad(1)\] массу цилиндра можно рассчитать, исходя из формулы $\displaystyle \rho=\frac \Rightarrow m=\rho V,$ где V – объем цилиндра, который можно вычислить по формуле \[V=\pi R^2 H\] Из формулы (1) выразим силу натяжения нити T: \[T=F_\text -mg=\rho_\text gV-\rho gV=Vg(\rho_\text -\rho)=\pi R^2 Hg(\rho_\text -\rho),\] где $\displaystyle \rho_\text $ – плотность воды, подставим в получившееся выражение численные значения: \[T=3,14\cdot0,25^2\text \cdot0,2\text \cdot 10\text /\text ^2 \cdot (1000\text /\text ^3-600\text /\text ^3)=157\text \]

Однородный кубический предмет с ребром $\displaystyle a=18$ см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна $\displaystyle \rho_\text =340$ кг/м $^3$ , плотность эфира $\displaystyle \rho_\text =720$ кг/м $^3$ . (Ответ дайте в сантиметрах.)

Запишем условие равновесия кубика на поверхности эфира: \[F_\text =mg, \quad(1)\] где $F_\text $ – выталкивающая сила, действующая на брусок, $\displaystyle m$ – масса кубика, которую можно рассчитать, исходя из формулы $\displaystyle \rho_\text =\frac \Rightarrow m=\rho_\text V,$ где V – объем кубика, который можно вычислить по формуле \[V=a^3.\] Выталкивающая сила равна: \[F_\text =\rho_\text gV_\text ,\] где $\displaystyle V_\text $ – объем погруженной части кубика, \[V_\text =xa^2,\] где $\displaystyle x$ – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: \[\rho_\text gxa^2=\rho_\text a^3\] \[\rho_\text x=\rho_\text a, \text x=\frac a> >.\] Пусть $\displaystyle y$ – длина части стороны, находящейся над эфиром, можем записать: \[y=a-x,\] искомая разница длин $\displaystyle \delta=y-x=a-2x=a-2\cdot \dfrac a> >=a(1-2\cdot \dfrac > >)$ подставим в получившееся выражение численные значения: \[\displaystyle \delta=0,18\text (1-2\cdot \dfrac /\text ^3> /\text ^3>)=0,01\text =1\text \]

В некий резервуар было налито 1000 литров жидкости плотностью $\displaystyle \rho_1=1500$ кг/м $^3$ . В этой жидкости в равновесии плавает кубик, погруженный в воду на $\displaystyle x=130$ см. Длина стороны кубика равна $\displaystyle a=200$ см. В сосуд доливают ещё 1000 литров жидкости плотностью $\displaystyle \rho_2=1100$ кг/м $^3$ и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)

В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. \[\rho_\text =\dfrac \] Так как кубик плавает на поверхности, то можно записать: \[mg=F_\text ,\] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна: \[F_\text =\rho_1 g V_\text ,\] где $\displaystyle V_\text =a^2x$ – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: \[F_\text =\rho_\text g V_\text =\dfrac g V_\text ,\] где $\displaystyle V_\text =a^2y$ – объем погруженной части куба до смешивания, $\displaystyle y$ – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим \[\rho_1 g a^2x=\dfrac g a^2y\] \[\rho_1x=\dfrac y,\] выразим отсюда y: \[y=\frac ,\] подставим в получившееся выражение численные значения: \[y=\frac /\text ^3 \cdot1,3\text > /\text ^3+1100\text /\text ^3>=1,5\text \]

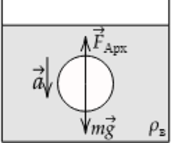
Стеклянный шарик опускается в воде с ускорением $\displaystyle a=6$ м/с $^2$ . Найти плотность стекла. Плотность воды $\displaystyle \rho_\text =1000$ кг/м $^3$ . Силами вязкого трения пренебречь. (Ответ дайте в кг/м $^3$ .)

При движении шарика в воде на него действует сила тяжести $\displaystyle m\vec g$ и сила Архимеда $\displaystyle F_\text $ . Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: \[\vec F_\text +m\vec g=m\vec a,\] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: \[mg- F_\text =ma,\] Отсюда с учетом выражения для силы Архимеда $\displaystyle F_\text =\rho_\text g V$ , где V – объем шарика, а
$\displaystyle \rho_\text $ – плотность воды, получим: \[mg- \rho_\text g V=ma,\] Выразим массу шарика: \[m=\frac g V> .\] Исходя из формулы, плотность стекла равна \[\displaystyle \rho_\text =\frac =\frac g V> =\frac g > ,\] подставим в получившееся выражение численные значения: \[\rho_\text =\frac /\text ^3\cdot 10\text /\text ^2 > /\text ^2-6\text /\text ^2>=2500\text /\text ^3\]

Однородный шарик, изготовленный из материала плотностью $\displaystyle \rho=2000$ кг/м $^3$ погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
$\displaystyle F_\text =100$ Н? (Ответ дайте в сантиметрах и округлите до целых.)

Выталкивающая сила равна по определению \[F_\text =\rho_\text gV_\text ,\] где $\displaystyle \rho_\text $ – плотность воды, $\displaystyle V_\text $ – объем погруженной части тела. Так как шар полностью опущен в воду, то \[V_\text =\frac43\pi R^3,\] где $\displaystyle R$ – радиус шара, получим: \[F_\text =\rho_\text g\frac43\pi R^3,\ (1)\] выразим из формулы R: \[R=\sqrt[3] > g\pi>>\] Подставив значения в формулу, получим: \[R=\sqrt[3] > /\text ^3\cdot10\text / \cdot3,14>> \approx0,13\text =13\text \]