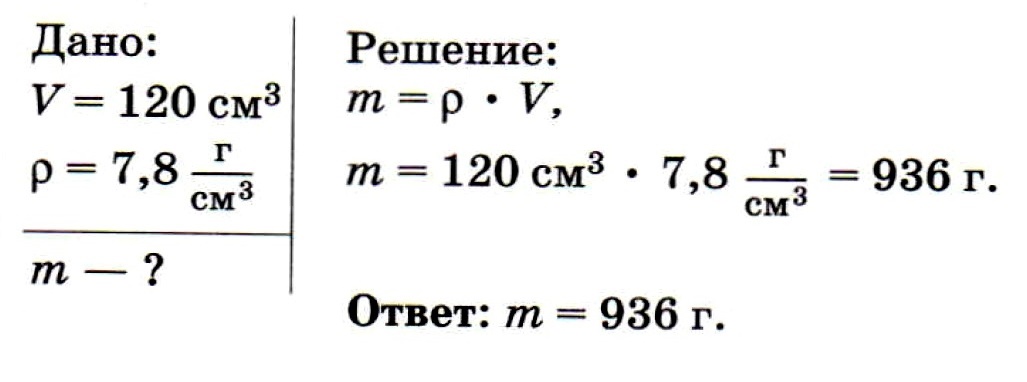Как определить плотность жидкости в которую погрузили цилиндр (6 видео)

Определение массы жидкостей, кроме непосредственного взвешивании. — с известной погрешностью можно производить объемным методом — с помощью пипеток, бюреток, мерных цилиндров, колб, мензурок и т. п. по формуле:

где m — масса жидкости, г; V — ее объем, см3; р—плотность жидкости, г/см3.

Плотность жидкостей и растворов находят по справочным таблицам или определяют самостоятельно. В лабораторной практике наибольшее распространение получили два метода определения плотности: 1) определение степени погружения денсиметра з жидкость; 2) взвешивание жидкости в сосуде известного объема.

При определении плотности с помощью денсиметр а последний погружают в цилиндр с жидкостью, термостатированной при определенной температуре, обычно при 20 или 15 °С. (рис. 25).

Для измерения температуры жидкости используют термометр с ценой деления не менее 0,5°С: неточность в измерении температуры в 1°С дает ошибку в значении плотности до 0,1%. Шкала денсиметров проградупрозана непосредственно в единицах плотности. Значение плотности жидкости считывают по делению шкалы, находящемуся на одном уровне с мениском жидкости.

Рис. 21. Определение плотности жидкости с помощью денсиметра.

Цена деления таких денсиметров 0,001 г/см3, а весь набор охватывает интервал плотностей от 0,700 до 1,840 г/см3. Иногда удобнее пользоваться приборами, шкала которых проградуирована в единицах концентрации для растворов определенных веществ. Такие приборы принято называть ареометрами.

В тех случаях, когда количество жидкости, находящейся в распоряжении экспериментатора, слишком мало, ее плотность определяют посредством пикнометров— небольших (от 1 до 100 мл) мерных колб.

На каждый находящийся в работе пикнометр должен быть нанесен номер титановым карандашом и заведена индивидуальная карточка, в которую закосят его точную массу (взвешивают чистый сухой пикнометр вместе с пробкой на аналитических весах) и значение «водной константы». Водная константа — эта масса воды в объеме пикнометра, приведенная к массе воды при 4 °С (температура, при которой плотность воды равна 1 г/см3).

С целью определения водной константы нового пикнометра его тщательно моют и заполняют предварительно прокипяченной (для удаления растворенного воздуха) дистиллированной водой немного выше метки.

Наполненный пикнометр выдерживают в течение 20 мин в водяном термостате при 20°С, после чего с помощью капилляра или тонких полосок фильтровальной бумаги отбирают лишнюю воду, доводя ее уровень в шейке пикнометра до метки по нижнему краю мениска. Верхнюю часть шейки пикнометра и шлиф протирают досуха кусочком фильтровальной бумаги, закрывают пикнометр пробкой, тщательно вытирают его снаружи, обсушивают 20—25 мин, после чего взвешивают на аналитических весах. Вычитая из массы пикнометра с водой массу сухого пикнометра получают массу воды в объеме пикнометра при 20 °С. Частное от деления полученного значения на 0,99823 г (масса 1 мл воды при 20 °С) и есть водная константа пикнометра.

При определении плотности какой-либо жидкости проделывают тс же операции, что и при определении водной константы. Для вычисления относительной плотности вещества d массу жидкости в объеме данного пикнометра делят на величину его водной константы

Содержание

Как определить плотность жидкости в которую погрузили цилиндр
Название величины
Обозначение
Единицы измерения
Формула
Масса
m = p * V
Объем
V = m / p
Плотность
кг/м 3
p = m / V
Физика 7 класс: все формулы и определения КРУПНО на трех страницах
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Справочный материал для «Задачи на плотность, массу и объем«
Гидростатика
🎬 Видео

Видео:Как измерить плотность металла (и любого твердого вещества)Скачать

Как определить плотность жидкости в которую погрузили цилиндр

Формулы, используемые в задачах по физике на плотность, массу и объем.

Название величины

Обозначение

Единицы измерения

Формула

Масса

m = p * V

Объем

V = m / p

Плотность

кг/м 3

p = m / V

Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

Физика 7 класс: все формулы и определения КРУПНО на трех страницах

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см 3 ?

Задача № 2. Определите объем кирпича, если его масса 5 кг?

Задача № 3. Определите массу стальной детали объёмом 120 см 3

Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м 3 ) меньше плотности стали (ρ₁ = 7800 кг/м 3 ). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

Задача № 5. Определите плотность мела, если масса его куска объемом 20 см 3 равна 48 г. Выразите эту плотность в кг/м 3 и в г/см 3 .

Читайте также: Топливная аппаратура маз 6 цилиндров

Ответ: Плотность мела 2,4 г/см 3 , или 2400 кг/м 3 .

Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м 2 ?

ОТВЕТ: 160 кг.

РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.

Вычисляем: m = 800 кг/м 3 • 0,04 м 2 • 5 м = 160 кг.

Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

РЕШЕНИЕ: Объем кубика V_K = а 3 = 216 см 3 . Объем стенок V_С можно вычислить, зная массу кубика m_К и плотность меди р: V_С = m_К / р = 91 см 3 . Следовательно, объем полости V_П = V_K — V_C = 125 см 3 . Поскольку 125 см 3 = (5 см) 3 , полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.

Задача № 9 (олимпиадный уровень). Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м 3

РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.

Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

Справочный материал для «Задачи на плотность, массу и объем«

Как, зная только массу, рассчитать плотность?

Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

Конспект урока «Задачи на плотность, массу и объем с решением».

Видео:Физика 7 класс (Урок№10 - Плотность и масса.)Скачать

Гидростатика

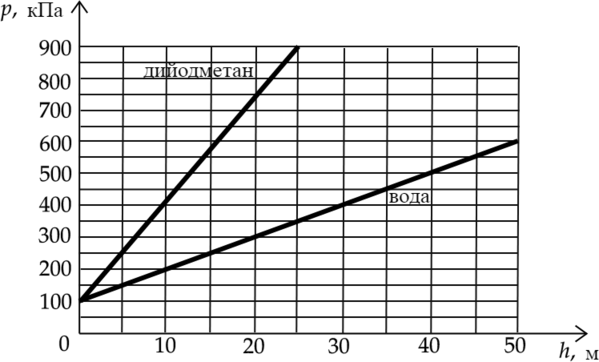
На рисунке представлены графики зависимости давления \(p\) от глубины погружения \(h\) для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
1) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
2) Плотность керосина 0,82 г/см \(^3\) , аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
3) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
4) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
5) Плотность оливкового масла 0,92 г/см \(^3\) , аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).

Читайте также: Опрос по теме цилиндр 11 класс

Полное давление \(p\) складывается из атмосферного давления \(p_a\) и гидростатического давления столба жидкости: \[p=\rho gh+p_a\] 1) Как видно из графика, давление воды на глубине 10 м принимает значение 200 кПа, что в два раза больше атмосферного давления (Атмосферное давление 100 кПа).
Утверждение 1 – \(\color >\)
2) Так как плотность керосина меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 2 – \(\color >\)
3) Давление в воде на глубине 25 м равно 350 кПа, что в 3,5 раза больше атмосферного.
Утверждение 3 – \(\color >\)
4) Так как прямая давления в дийодметане лежит выше прямой давления в воде, то это означает, что давление в дийодметане возрастает быстрее, чем в воде.
Утверждение 4 – \(\color >\)
5) Так как плотность оливкого масла меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 5 – \(\color >\)

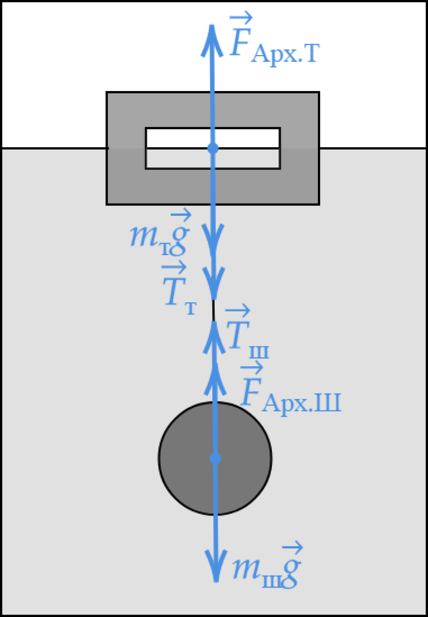
К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см \(^3\) , плотность жидкости 800 кг/м \(^3\) , объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите два верных утверждения.
1) Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.
2) Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.
3) Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.
4) Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.
5) Объём погружённой части тела равен четверти объёма этого тела.

Запишем первый закон Ньютона для тела и шарика: \[F_ >-m_ >g-T=0\] \[F_ >-m_ >g+T=0\]
Сложим два уравнения: \[F_ >-m_ >g+F_ >-m_ >g=0\]
Обозначим плотность жидкости \(\rho_1\) , плотность материала \(\rho_2=2\rho_1\) \[\rho_1gV_1-\rho_2\cdot \frac V_ g+\rho_1 g \cdot \frac V_ -\rho_2\cdot \frac V_ g=0\] \[\rho_1V_1-2\rho_1\cdot \frac V_ +\rho_1 \cdot \frac V_ -2\rho_1\cdot \frac V_ =0\] \[V_1-2\cdot \frac V_ + \frac V_ -2\cdot \frac V_ =0\] \[V_1=\frac V_T\]
Тело плавает, погруженное на 3/4 своего объёма.
1) Сила Архимеда, действующая на тело, равна \(\displaystyle F_ >=\rho_1g\frac V_T\) , а сила Архимеда, действующая на шар \(\displaystyle F_ >=\rho_1g\frac V_T\) .
Утверждение 1 – \(\color >\)
2) \[T=m_ >g-F_ >\]
Утверждение 2 – \(\color >\)
3) \[T=F_ >-m_ >g\]
Утверждение 3 – \(\color >\)
4) Модуль силы тяжести тела: \[m_ >g=\rho_2\cdot \frac V_ g\] Модуль силы тяжести шарика: \[m_ >g=\rho_2\cdot \frac V_ g\]
Утверждение 4 – \(\color >\)
5) Объём погружённой части тела равен \(\dfrac \) объёма этого тела.
Утверждение 5 – \(\color >\)

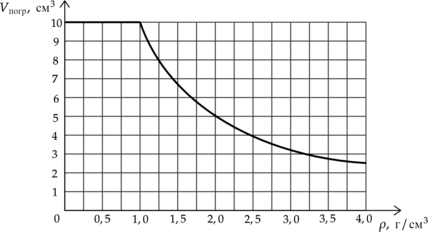
Ученик помещал цилиндр, не удерживая его, в различные жидкости, плотности которых представлены в таблице, и измерял объем погруженной в жидкость части цилиндра \(V_\text \) . По результатам измерений он получил зависимость, представленную на графике объема погруженной части цилиндра \(V_\text \) от плотности жидкости \(\rho\) . Объем цилиндра постоянен и равен \(V=10\) см \(^3\)

\[\begin \hline \text &\text &\text &\text &\text &\text &\text &\text \\ \hline \text &0,71&0,79&1,0&1,26&1,49&2,89&3,25\\ \hline \end \]
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) В бензине и воде сила Архимеда, действующая на цилиндр, одинакова.
2) Цилиндр не тонет в глицерине.
3) На цилиндр, погруженный в бромоформ, действует сила Архимеда 200мН.
4) Цилиндр плавает во всех жидкостях, указанных в таблице.
5) При плавании цилиндра в глицирине и бромоформе сила Архимеда, действующая на него, одинакова.

Читайте также: Цилиндр поворотный камаз 65201

1) В бензине и в спирте цилиндр погружен на одинаковый объем. В таком случае сила Архимеда равна \[F_A=\rho gV_\text ,\] где \(\rho\) – плотность жидкости, в которую погружено тело.
Но плотность спирта больше плотности бензина, а значит и сила Архимеда, действущая на цилиндр в спирте, больше силы Архимеда, действующей на цилиндр в бензине.
Утверждение 1 – \(\color >\)
2) Цилиндр тонет при плотности меньше, чем 1 г/см \(^3\) , у глицирина плотность 1,26 г/см \(^3\) , значит, цилиндр плавает.
Утверждение 2 – \(\color >\)
3) У бромоформа плотность больше 1 г/см \(^3\) , а значит сила Архимеда уравновешивает силу тяжести.
По графику видим, что цилиндр начинает плавать при плотности жидкости 1г/см \(^3\) , а значит именно такова плотность материала, из которого он сделан. Откуда сила Архимеда, действующая на цилиндр \[F_A=mg=1\text \cdot 10\text \cdot 10\text =100\text \] Утверждение 3 – \(\color >\)
4) Нет, при плотности меньше 1 г/см3 цилиндр не плавает.
Утверждение 4 – \(\color >\)
5) У глицирина и бромоформа плотность больше 1 г/см \(^3\) , а значит сила Архимеда уравновешивает силу тяжести и силы Архимеда одинаковы.

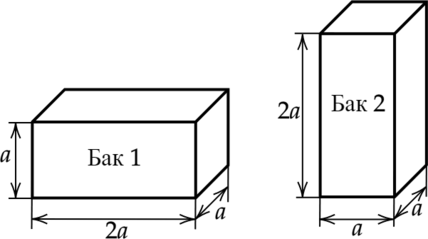
На полу лифта расположены два одинаковых металлических бака, в которых доверху налита вода (см. рисунок).

Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Давление воды на дно первого бака в 4 раза меньше, чем на дно второго.
2) Первый бак давит на пол лифта с силой, в 2 раза меньшей, чем второй.
3) Сила давления воды на дно первого бака в 2 раза меньше, чем на дно второго.
4) Первый бак оказывает на пол лифта в 2 раза меньшее давление, чем второй.
5) Если лифт начнёт движение вниз с ускорением 2 м/с \(^2\) , давление воды на дно баков уменьшится на 20 %.

1) Давление воды на дно первого бака равно \[\displaystyle p_1=\frac \] где \(m\) — масса воды. Давление на дно второго бака \[\displaystyle p_2=\frac \] Видно, что давление \(p_2=2p_1\) , следовательно, давление воды на дно первого бака в 2 раза меньше, чем на дно второго бака.
Утверждение 1 – \(\color >\)
2) Сила давления равна силе тяжести воды. Так как объем одинаковый, значит масса воды в сосудах одинаковая.
Утверждение 2 – \(\color >\)
3) Утверждение 3 – \(\color >\)
4) Утверждение 4 – \(\color >\)
5) При движении лифта вниз с ускорением 2 м/с \(^2\) , оно будет компенсировать ускорение свободного падения \(g\) , то есть вода будет иметь ускорение свободного падения 10-2=8 м/с \(^2\) . В результате сила давления на дно баков будет равна \(F=8m\) .
Утверждение 5 – \(\color >\)

В сосуд с жидкостью погружают маленький датчик манометра, который регистрирует давление, создаваемое только столбом жидкости (без учёта атмосферного давления). На рисунке представлен график зависимости показаний \(p\) этого датчика давления от времени \(t\) . Известно, что датчик может либо двигаться строго по вертикали вниз со скоростью 1 мм/с, либо покоиться.
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) Максимальная глубина погружения датчика давления равна 20 см.
2) В промежутке времени от 50 с до 150 с датчик давления находился на одной и той же глубине.
3) Плотность жидкости, в которую опустили датчик давления, равна 650 кг/м \(^3\) .
4) Максимальная глубина погружения датчика давления равна 15 см.
5) Плотность жидкости, в которую опустили датчик давления, равна 1300 кг/м \(^3\) .

1) Датчик двигался на промежутках от 0 с до 50 с и от 150 с до 200 с, т. е. глубина погружения \(h=1 \cdot (50 + 50 ) = 100\) мм \(= 10\) см.
Утверждение 1 – \(\color >\)
2) Из графика видно, что давление не изменяется в промежутке времени от 50 с до 150 с, это означает что датчик находился на одной и той же глубине, т. е. покоился.
Утверждение 2 – \(\color >\)
3) Давление столба жидкости: \[p=\rho gh\] Плотность жидкости: \[\rho=\frac

=\frac =1300 \text \]
Утверждение 3 – \(\color >\)
4) Глубина погружения 10 см
Утверждение 4 – \(\color >\)
5) Плотность жидкости \(\rho=1300\) кг/м \(^3\)
Утверждение 5 – \(\color >\)