Как определить радиус инерции однородного цилиндра

Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Момент инерции для чайников: определение, формулы, примеры решения задач

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Видео:Урок 94. Вычисление моментов инерции телСкачать

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Видео:Расчет момента инерции цилиндраСкачать

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Видео:Момент инерции абсолютно твердого тела. 10 класс.Скачать

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

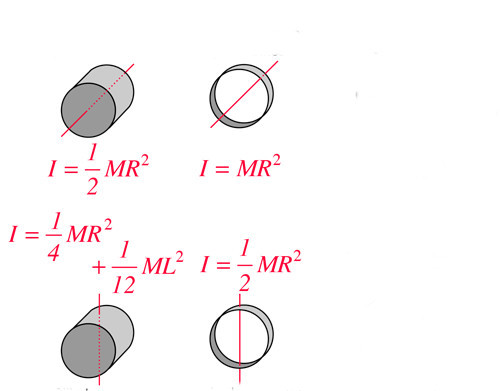
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Видео:момент инерции цилиндраСкачать

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Читайте также: Как загнуть фанеру в цилиндр

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Видео:13. Вычисление момента инерцииСкачать

Момент инерции цилиндра сплошного и полого относительно разных осей. Пример задачи

Как известно, масса в динамике поступательного движения играет важную роль, определяя инерционные свойства движущихся тел. В динамике вращения вместо массы пользуются моментом инерции. Рассмотрим в статье, что это за величина и как определяется момент инерции цилиндра относительно оси.

Видео:5. Момент инерции простейших телСкачать

Что такое момент инерции?

Эту величину обычно обозначают буквой I. Для материальной точки математическая формула момента инерции записывается так:

Где r — расстояние до оси вращения от точки массой m. Из формулы понятно, что единицей измерения величины являются килограммы на квадратный метр (кг*м 2 ).

Если тело имеет сложную форму и его объемная плотность является переменной, тогда для определения I следует использовать такое интегральное выражение:

Где dm — это элементарная масса, находящаяся от оси вращения на расстоянии r.

Таким образом, момент инерции определяет распределение материи в теле сложной формы относительно конкретной оси вращения системы.

Видео:Момент инерцииСкачать

Сплошной цилиндр и главная ось

Момент инерции сплошного цилиндра может быть вычислен вокруг абсолютно любой оси с использованием интегрального выражения, записанного в предыдущем пункте. Здесь рассмотрим ситуацию, когда цилиндр массой M, радиусом R и высотой L вращается вокруг главной оси. Последняя представляет собой прямую, параллельную генератрисе фигуры и проходящую через центры ее круглых оснований.

Не будем вдаваться в подробности математических вычислений по интегральной формуле, а приведем сразу конечное выражение:

Мы видим, что чем больше масса цилиндра и его радиус, тем больше момент инерции I₁. В то же время эта величина никак не зависит от высоты фигуры L, то есть момент инерции тонкого диска можно вычислить также по этой формуле.

Отметим, что если всю массу цилиндра собрать в одну материальную точку, находящуюся от оси вращения на расстоянии радиуса R, то для нее момент инерции окажется в два раза больше, чем для сплошного цилиндра.

Видео:Найти момент инерции тонкого однородного стержня: Волькенштейн 3.5Скачать

Однородный цилиндр и перпендикулярная генератрисе ось

Теперь возьмем однородный цилиндр из примера выше и перевернем его на бок. Начнем вращать объект вокруг оси, которая проходит также через центр его масс, но уже перпендикулярна генератрисе (главной оси). Чему будет равен момент инерции цилиндра однородного в данном случае?

Как и в примере выше, здесь также ограничимся приведением соответствующего выражения. Оно будет иметь следующий вид:

Момент инерции I₂ имеет более сложную зависимость от параметров цилиндра, чем I₁, поскольку он определяется не только массой и радиусом, но и высотой фигуры. Заметим, что два слагаемых этой формулы представляют собой два крайних случая:

• Если цилиндр слишком маленькую высоту имеет, то мы получаем диск, который, вращаясь вокруг оси, проходящей через его диаметр, будет иметь момент 1/4*M*R 2 .
• Если радиус цилиндра стремится к нулю, то рассматриваемый объект превратится в стержень, и его момент инерции станет равным 1/12*M*L 2 .

Читайте также: В чем различия главных тормозных цилиндров

Видео:Радиус инерции. Момент сопротивленияСкачать

Полый цилиндр

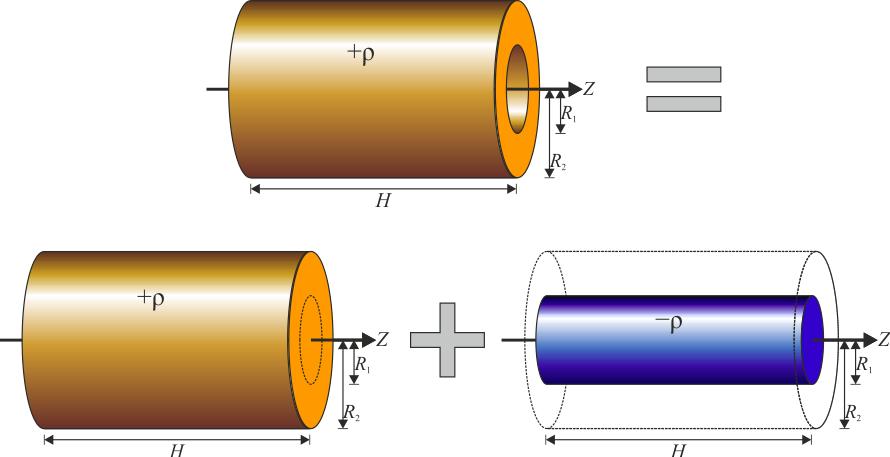
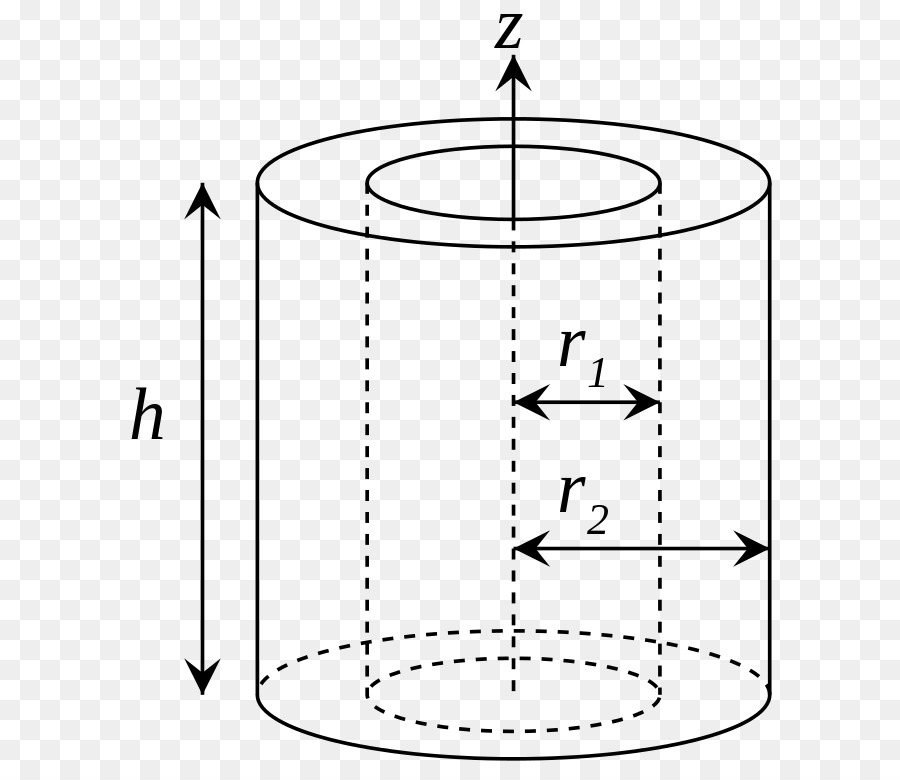
Выше мы рассмотрели, как рассчитывать момент инерции цилиндра вращающегося и однородного. Теперь предположим, что высота цилиндра и его масса остались теми же самыми, однако он стал полым, то есть, имеет два радиуса: внешний R₁ и внутренний R₂.

Применение все той же интегральной формулы позволяет получить выражение для момента инерции цилиндра полого, который вращается вокруг своей главной оси. Соответствующая формула выглядит так:

Это выражение позволяет сделать важный вывод: при одинаковых массах полого и сплошного цилиндров первый обладает большим моментом инерции. Связан этот факт с тем, что большая часть массы полого цилиндра находится дальше от оси вращения, а как видно из формул, от радиуса изучаемая величина растет квадратично.

Видео:2 а Моменты инерции сферы и шараСкачать

Где используются знания величин I для цилиндров?

Пожалуй, основной областью применения изложенной выше теории является автомобильная промышленность. В частности, коленчатый вал автомобиля снабжен тяжелым сплошным маховиком, имеющим цилиндрическую форму. Необходим маховик для того, чтобы обеспечить максимальную плавность вращения коленчатого вала, что отражается на плавности автомобильного хода. Маховик гасит любые большие угловые ускорения как во время разгона транспортного средства, так при его торможении.

Из формулы выше для момента инерции I₁ понятно, что для увеличения этой величины выгоднее увеличить радиус, чем массу цилиндра (маховика). Так, удвоение массы приведет лишь к удвоению момента инерции. Однако если увеличить в два раза радиус, то I₁ возрастет аж в 4 раза, что обеспечит более эффективное использование маховика.

Видео:Нахождение момента инерции стержня путем интегрированияСкачать

Пример решения задачи

Прежде чем решать задачу, скажем несколько слов о динамике вращения. Как и в динамике поступательного движения, в ней существует формула, подобная второму закону Ньютона. Эта формула называется уравнением моментов. Записывается она так:

Где L — момент импульса, M — момент внешних сил. Чаще всего это уравнение записывают в следующем виде:

Здесь α — ускорение угловое. Из этого выражения видна аналогия со вторым ньютоновским законом.

Теперь перейдем к решению задачи. Известно, что сила в 100 Н действует по касательной к цилиндрической поверхности перпендикулярно главной оси вращения сплошного цилиндра на расстоянии 20 см. Масса цилиндра равна 10 кг, а его радиус составляет 20 см. Необходимо определить угловую скорость ω цилиндра через 5 секунд после начала действия силы.

Угловая скорость рассчитывается по формуле для равноускоренного движения:

Выражая ускорение из уравнения моментов и подставляя его в выражение, получим:

Момент силы вычисляется так:

Где по условию задачи d = R. Подставляя это выражение и выражение для I сплошного цилиндра, получим конечную рабочую формулу:

Осталось сюда подставить все величины в единицах СИ и записать ответ: ω = 500 рад/с, что равно приблизительно 80 оборотам в секунду.

Видео:Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Общие теоремы динамики

В разделе «Общие теоремы динамики» изучают четыре основных теоремы:

Сначала рассмотрим случаи применения каждой из них:
1. В задаче отсутствует вращение тела вокруг неподвижной оси. Первым делом в таких задачах необходимо посмотреть, можно ли приравнять
проекцию суммы внешних сил на какую-либо ось к нулю. Если да, то применяем теорему об изменении количества движения.
2. Когда в задаче главным объектом является вращающееся вокруг неподвижной оси тело. Первым делом в таких задачах необходимо посмотреть,
можно ли приравнять сумму моментов внешних сил относительно оси вращения к нулю. Если да, то применяем теорему об изменении кинетического
момента.

Читайте также: Как найти площадь боковой стороны цилиндра

Если к нулю ничего не приравнивается, то, как правило, и для 1 и для 2 типов задач решение проще получить с помощью теоремы об изменении
кинетической энергии, причем, если в задаче теребуется определить ω(x) или V(x), то применяем теорему об изменении кинетической энергии
в интегральной форме, а если нужно найти a(V) или ε(V), то применяем теорему об изменении кинетической энергии в дифференциальной
форме.

Эллиптический маятник состоит из тела А массы М, которое может перемещаться по гладкой горизонтальной плоскости и груза В массы m, связанного с телом А невесомым стержнем АВ длиной l. В начальный момент времени стержень был отклонен на угол φ₀ и отпущен без начальной скорости. Определить смещение тела А в зависимости от угла φ.

Шарик А массы m движется из вершины кругового конуса без начальной скорости по желобу, расположенному вдоль его образующей. В начальный момент времени угловая скорость конуса равна ω₀. Определить угловую скорость конуса в момент, когда шарик достигнет его основания. Конус вращается вокруг оси Z без трения. Момент инерции конуса относительно его оси вращения I_z = 3mr 2 .

По горизонтальной платформе 1 массой М, движущейся по инерции со скоростью v₁, перемещается тележка 2 массой m с постоянной относительной скоростью v₂. В некоторый момент времени тележка была заторможена. Определить общую скорость u платформы с тележкой после ее остановки.

Два человека равной массы m стоят на концах горизонтального стержня АВ с той же массой, вращающегося вокруг вертикальной оси Оz, проходящей через середину стержня, с угловой скоростью ω₀. Как изменится угловая скорость стержня, если оба человека займут положение на серединах отрезков ОА и ОВ?

Однородный стержень АВ вместе с грузом массы m, прикрепленным к стержню при помощи нити АА₁, вращается вокруг вертикальной оси Oz с угловой скоростью ω₀. В некоторый момент нить пережигается. Определить угловую скорость стержня как функцию расстояния х от оси вращения. Длина нити АА₁ равна l. Момент инерции стержня относительно оси Oz равен I. Груз считать материальной точкой.

На палубе авианосца массой М, движущегося с постоянной скоростью V, находится самолет массы m. Пренебрегая сопротивлением воды, определить как изменяется скорость авианосца при разгоне самолета по палубе. Скорость самолета относительно авианосца при разгоне u = kr 2 , где k = const.

Однородный диск радиуса r и массой m катится без скольжения по горизонтальной плоскости. Начальная скорость его центра равна V_O. Какое расстояние S пройдет центр катка до остановки, если коэффициент трения качения равен δ?

Вал ворота радиуса r приводится в движение постоянным вращающим моментом М, приложенным к рукоятки АВ. Определить ускорение груза С массой m₁, если коэффициент трения скольжения груза о горизонтальную плоскость равен f. Масса вала равна m₂. Массой рукоятки и трением в оси ворота пренебречь. Вал считать однородным цилиндром.

Пара сил с постоянным моментом М приводит в движение кривошип 1 кривошипно-ползунного механизма, расположенного в горизонтальной плоскости. В момент времени, когда ∠АОВ = 90 0 точка А имеет скорость u. Кривошип 1 и шатун 2 представляют собой однородные стержни массами m₁ = m и m₂ = 2m соответственно. Пренебрегая массой ползуна 3 и трением, найти скорость точки А в тот момент, когда ползун 3 займет крайнее правое положение.

🔍 Видео

Определение моментов инерции твёрдых тел методом крутильных колебаний (лабораторная работа М30)Скачать

1.257бСкачать

Объем и момент инерции однородного шараСкачать

Расчет момента инерции диска или цельного цилиндраСкачать

Расчет момента инерции тонкого стержняСкачать

Механика вращательного движения [Физзадачи #35]Скачать

Вычисление момента инерции тел с помощью интеграла (стержень, круг, цилиндр)Скачать