- ГДЗ учебник по физике 7 класс Перышкин. №1 Определение цены деления измеррительного прибора. Номер №1
- Решение
- ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
- Решение
- Погрешности измерений, представление результатов эксперимента
- п.1. Шкала измерительного прибора
- п.2. Цена деления
- п.3. Виды измерений
- п.4. Погрешность измерений, абсолютная и относительная погрешность
- п.5. Абсолютная погрешность серии измерений
- п.6. Представление результатов эксперимента
- п.7. Задачи
- 🎬 Видео
Видео:Определение цены деления измерительного цилиндра, определение с его помощью объема жидкости.Скачать

ГДЗ учебник по физике 7 класс Перышкин. №1 Определение цены деления измеррительного прибора. Номер №1
Цель работы:
Определить цену деления измерительного цилиндра (мензурки), научиться пользоваться им и определять с его помощью объём жидкости.
Приборы и материалы:
Измерительный цилиндр (мензурка), стакан с водой, небольшая колба и другие сосуды.
Указания к работе:
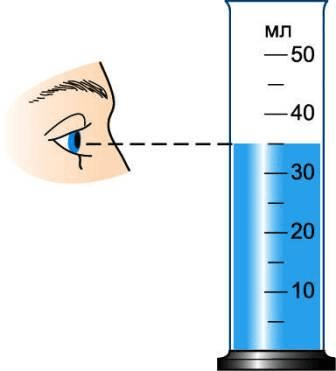
1 . Рассмотрите измерительный цилиндр (рис. 198 ), обратите внимание на его деления. Ответьте на следующие вопросы.
1 )Какой объём жидкости вмещает измерительный цилиндр, если жидкость налита:
а) до верхнего штриха;
б) до первого снизу штриха, обозначенного цифрой, отличной от нуля?
2 )Какой объём жидкости помещается:
а) между 2 −м и 3 −м штрихами, обозначенными цифрами;
б) между соседними (самыми близкими) штрихами мензурки?
2 . Как называется последняя вычисленная вами величина? Как определяют цену деления шкалы измерительного прибора?
Запомните: прежде чем проводить измерения физической величины с помощью измерительного прибора, определите цену деления его шкалы.
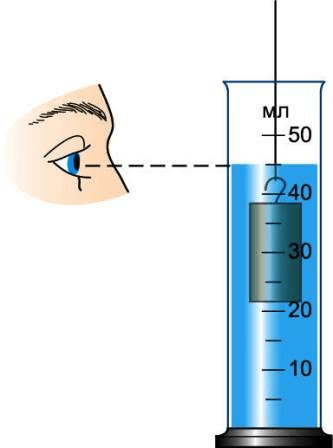
3 . Рассмотрите рисунок 7 учебника и определите цену деления изображённой на нём мензурки.
4 . Налейте в измерительный цилиндр воды, определите и запишите, чему равен объём налитой воды.
Примечание. Обратите внимание на правильное положение глаза при отсчёте объёма жидкости. Вода у стенок сосуда немного приподнимается, в средней же части сосуда поверхность жидкости почти плоская. Глаз следует направить на деление, совпадающее с плоской частью поверхности (рис. 198 ).
5 . Налейте полный стакан воды, потом осторожно перелейте воду в измерительный цилиндр. Определите и запишите с учётом погрешности, чему равен объём налитой воды. Вместимость стакана будет такой же.
6 . Таким же образом определите вместимость колбы, аптечных склянок и других сосудов, которые находятся на вашем столе.
7 . Результаты измерений запишите в таблицу 6 .
рис. 198 .
рис. 7 . Измерительный цилиндр.
Таблица 6 .
Решение
Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл.
1 .
1, а) Если жидкость налита до верхнего штриха, измерительный цилиндр вмещает 50 мл жидкости.
1, б) Если жидкость налита до первого снизу штриха, обозначенного цифрой, отличной от нуля, измерительный цилиндр вмещает 10 мл жидкости.
2, а) Между 2 − м и 3 −м штрихами, обозначенными цифрами, помещается 10 мл жидкости (например, возьмём штрихи 20 мл и 30 мл).
2, б) Между соседними (самыми близкими) штрихами мензурки (например, возьмём штрихи 30 и 35 ), помещается 5 мл жидкости.
2 . Последняя вычисленная нами величина является ценой деления измерительного цилиндра.
3 . На шкале цилиндра возьмём, к примеру, числа 50 и 60 . Количество маленьких штрихов между этими числами − 2 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл.
4 . Объём налитой воды равен 35 мл или 35 $см^ $ .
5 . Погрешность измерений равна половине цены деления шкалы измерительного прибора. Цена деления цилиндра − 5 мл, следовательно, погрешность измерения равна $\frac $ мл = 2,5 мл.
Объём налитой в полный стакан воды с учётом погрешности будет равен ( 200 ±∆ 2,5 ) мл ( $см^ $ ).
6 .
Таблица 6 .
| № опыта |Название сосуда| Объём жидкости $V_ , см^ $ |Вместимость сосуда, $V_ , см^ $ |
| −−− | −−− | −−− | −−− |
| 1 | стакан | 200 | 200 |
| 2 | колба | 50 | 50 |
| 3 | пузырёк | 30 | 30 |
Читайте также: Обнаружены пропуски воспламенения в 4 цилиндре что это
Вывод. В ходе лабораторной работы мы определелили цену деления измерительного цилиндра, научились им пользоваться и научились с его помощью определять объём жидкости.
Видео:Как определить цену деления измерительного прибораСкачать

ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1 . Определите цену деления мензурки.
2 . Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
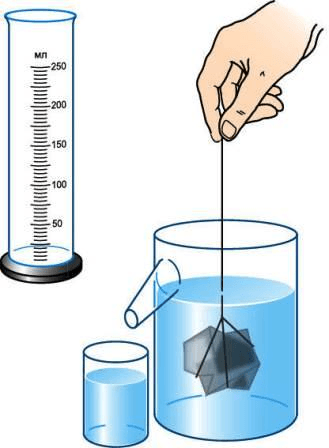
3 . Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201 ), и снова измерьте объём жидкости.
4 . Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5 . Результаты измерений запишите в таблицу 9 .
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202 ). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.
Таблица 9 .
рис. 201
рис. 202
Решение
Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
$V = V_ — V_ $ , где $V_ $ − объём воды и тела, $V_ $ − начальный объём воды в мензурке.
- Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл. - В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70 $см^ $ .
- Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
$V_ = 95 — 70 = 25 см^ $
$V_ = 85 — 65 = 20 см^ $
$V_ = 75 — 60 = 15 см^ $ - Результаты измерений запишем в таблицу 9 .
Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.
Видео:Определение показаний прибораСкачать

Погрешности измерений, представление результатов эксперимента
п.1. Шкала измерительного прибора
Примеры шкал различных приборов:
 Манометр – прибор для измерения давления, круговая шкала |  Вольтметр – прибор для измерения напряжения, дуговая шкала |  Индикатор громкости звука, линейная шкала |
п.2. Цена деления
Пример определения цены деления:
п.3. Виды измерений
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Определяется субъективным фактором, ошибками экспериментатора.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 | Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: \begin \triangle=\frac = \frac > =0,5\ \text \end Инструментальная погрешность: \begin d=\frac =\frac =0,25\ \text \end Истинное значение: \(L_0=4\ \text \) Результат измерений: $$ L=L_0\pm d=(4,00\pm 0,25)\ \text $$ Относительная погрешность: $$ \delta=\frac \cdot 100\text =6,25\text \approx 6,3\text $$ |
 | Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: \begin \triangle=\frac = \frac > =0,1\ \text \end Инструментальная погрешность: \begin d=\frac =\frac =0,05\ \text \end Истинное значение: \(L_0=4,15\ \text \) Результат измерений: $$ L=L_0\pm d=(4,15\pm 0,05)\ \text $$ Относительная погрешность: $$ \delta=\frac \cdot 100\text \approx 1,2\text $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
Сначала находим среднее значение всех измерений: \begin m_0=\frac =\frac \approx 100,4\ \text \end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin \triangle_1=|100,4-99,8|=0,6\\ \triangle_2=|100,4-101,2|=0,8\\ \triangle_3=|100,4-100,3|=0,1 \end Находим среднее абсолютное отклонение: \begin \triangle_ =\frac =\frac =0,5\ \text \end Мы видим, что полученное значение \(\triangle_ \) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: \begin \triangle m=max\left\ ; d\right\>=max\left\ \ \text \end Записываем результат: \begin m=m_0\pm\triangle m\\ m=(100,4\pm 0,5)\ \text \end Относительная погрешность (с двумя значащими цифрами): \begin \delta_m=\frac \cdot 100\text \approx 0,050\text \end
п.6. Представление результатов эксперимента
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | \(\triangle=\frac \), мл |
| 1 | 20 | 40 | 4 | \(\frac =4\) |
| 2 | 100 | 200 | 4 | \(\frac =20\) |
| 3 | 15 | 30 | 4 | \(\frac =3\) |
| 4 | 200 | 400 | 4 | \(\frac =40\) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем \(V_0\), мл | Абсолютная погрешность \(\triangle V=\frac \), мл | Относительная погрешность \(\delta_V=\frac \cdot 100\text \) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0\pm 0,1)\ \text ,\ \ x_2=(4,0\pm 0,03)\ \text $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: \begin \delta_1=\frac \cdot 100\text =2,5\text \\ \delta_2=\frac \cdot 100\text =0,75\text \end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ \triangle v_1=\frac =5\ (\text ),\ \ \triangle v_2=\frac =0,5\ (\text ) $$ Показания каждого из спидометров: $$ v_1=(54\pm 5)\ \text ,\ \ v_2=(72\pm 0,5)\ \text $$ Скорость сближения равна сумме скоростей: $$ v_0=v_ +v_ ,\ \ v_0=54+72=125\ \text $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ \triangle v=\triangle v_1+\triangle v_2,\ \ \triangle v=5+0,5=5,5\ \text $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0\pm 5,5)\ \text $$ Относительная погрешность: $$ \delta_v=\frac \cdot 100\text \approx 4,4\text $$ Ответ: \(v=(126,0\pm 5,5)\ \text ,\ \ \delta_v\approx 4,4\text \)
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки \(d=\frac =0,05\ \text \)
Результаты прямых измерений длины и ширины: $$ a=(90,20\pm 0,05)\ \text ,\ \ b=(60,10\pm 0,05)\ \text $$ Относительные погрешности (не забываем про правила округления): \begin \delta_1=\frac \cdot 100\text \approx 0,0554\text \approx \uparrow 0,056\text \\ \delta_2=\frac \cdot 100\text \approx 0,0832\text \approx \uparrow 0,084\text \end Площадь столешницы: $$ S=ab,\ \ S=90,2\cdot 60,1 = 5421,01\ \text ^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ \delta_S=\delta_a+\delta_b=0,056\text +0,084\text =0,140\text =0,14\text $$ Абсолютная погрешность: \begin \triangle S=S\cdot \delta_S=5421,01\cdot 0,0014=7,59\approx 7,6\ \text ^2\\ S=(5421,0\pm 7,6)\ \text ^2 \end Ответ: \(S=(5421,0\pm 7,6)\ \text ^2,\ \ \delta_S\approx 0,14\text \)
🎬 Видео
Упр 1.2 - Физика 7 класс ПёрышкинСкачать

Цена деления, погрешность и объем жидкости в мензуркеСкачать

7 класс. Определение цены деления измерительного прибора и погрешности его измерения.Скачать

"Определение цены деления измерительного прибора" - Л/б, 7 класс А.В. ПерышкинСкачать

КАК ИЗМЕРИТЬ ЦИЛИНДРЫ? Учимся пользоваться нутромером и микрометромСкачать

Лабораторная работа № 1 Определение цены деления шкалы измерительного прибораСкачать

Урок 4 (осн). Измерение физических величин. Цена деления шкалы измерительного прибораСкачать

Лабораторная работа №1 Определение цены деления измерительного прибораСкачать

определение цены деления прибораСкачать

Определение цены деления измерительного прибораСкачать

Микрометр и нутромер. Как измерить цилиндры?Скачать

цена деленияСкачать

Укажите предел измерения и цену деления измерительного цилиндра, представленного на рисунке - №28803Скачать
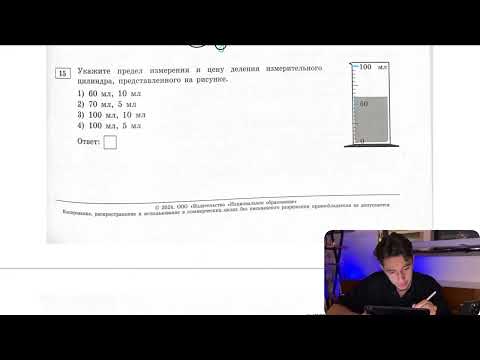
Укажите предел измерения и цену деления измерительного цилиндра, представленного на рисунке - №28803Скачать

Определение цены деления и погрешности. Физика 7 класс.Скачать

Примеры задач (Предел измерений и цена деления #2)| ФизикаСкачать

Предел измерений и цена деления #1| ФизикаСкачать