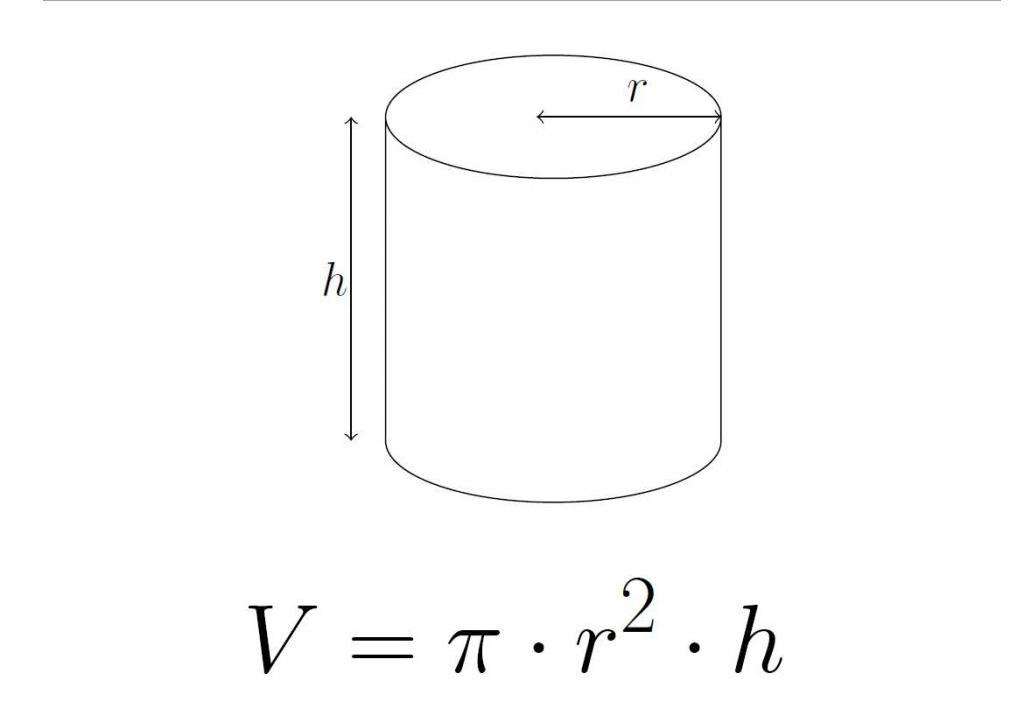Как посчитать объем цилиндра в миллилитрах

Калькулятор объема минераловатных цилиндров позволяет перевести м.п в м 3 , что легко позволит подобрать требуемый тип автомобиля для транспортной доставки.

Видео:Цилиндр - расчёт площади, объёма.Скачать

Онлайн-калькулятор для расчёта объёма цилиндра

Особый тип теплоизоляционного оборудования — минераловатные цилиндры. Чаще всего они применяются для тепловой, звуковой и вибрационной изоляции газоходов, трубопроводов и дымовых труб. Такие цилиндры производят из минеральной ваты, которая уже продемонстрировала свои высокие эксплуатационные характеристики. Сама минеральная вата, в свою очередь, состоит из синтетических элементов и волокон горных пород. Для того чтобы улучшить теплоизоляционные качества минеральной ваты, материал нередко покрывают специальной алюминиевой фольгой.

Преимущества минераловатных цилиндров

Минераловатные цилиндры отличаются практически уникальными техническими параметрами, к которым относятся:

• невозможность возгорания;
• стойкость к механическим нагрузкам;
• отсутствие токсичности;
• водонепроницаемость;
• стойкость по отношению к химическим веществам;
• экологичность;
• долговечность.

Минераловатные цилиндры просты в монтаже и обслуживании, однако, разумеется, такие материалы требуют транспортировки. Несмотря на то, что сама по себе минеральная вата не такая уж и тяжёлая, необходимо правильно выбрать способ её перемещения и доставки. Лучшим решением будет онлайн калькулятор для расчёта объёма цилиндра.

Как использовать онлайн калькулятор объёма цилиндра?

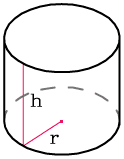
Компания «Верное решение» не только поможет вам выбрать подходящие теплоизоляционные материалы, но и предоставит бесплатный онлайн калькулятор объёма цилиндра по формуле. Согласно математическим законам, объём любого цилиндра можно вычислить, зная либо площадь основания, либо его радиус. Формула, которой руководствуется калькулятор объёма цилиндра, выглядит следующим образом:

V = πr²h, где r — радиус и h — длина трубы.

Наша компания предлагает использовать онлайн калькулятор объёма цилиндра через диаметр, который, как известно, в два раза больше радиуса.

Особое удобство, которым может похвастаться онлайн калькулятор объёма цилиндра в м3, заключается в том, что система расчёта, которую разработала компания «Верное решение», способна превратить онлайн калькулятор объёма цилиндра в литрах в калькулятор объёма цилиндра в м3. Такое измерение является более подходящим при выборе правильного транспортного средства для доставки материала на место.

Видео:Объём цилиндраСкачать

Как посчитать объем цилиндра

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ ( 1 /₂) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см 2 , то:

Читайте также: Как найти площадь основания цилиндра если известна площадь боковой поверхности

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см 2 , то:

V = 30 2 / _{4 ⋅ 3.14⋅ 5} = 900 /_62.8 = 14.33 см 3

Видео:Объем цилиндра.Скачать

Формула объема цилиндра: пример решения задачи

Объем является физической величиной, которая присуща телу с ненулевыми размерами вдоль каждого из трех направлений пространства (все реальные объекты). В статье в качестве примера формулы объема рассматривается соответствующее выражение для цилиндра.

Видео:11 класс, 32 урок, Объем цилиндраСкачать

Объем тел

Эта физическая величина показывает, какую часть пространства занимает то или иное тело. Например, объем Солнца намного больше этой величины для нашей планеты. Это означает, что принадлежащее Солнцу пространство, в котором находится вещество этой звезды (плазма), превышает земную пространственную область.

Объем изменяется в кубических единицах длины, в СИ это метры в кубе (м3). На практике объемы жидких тел измеряют в литрах. Маленькие объемы могут выражать в кубических сантиметрах, миллилитрах и других единицах.

Для вычисления объема формула будет зависеть от геометрических особенностей рассматриваемого объекта. Например, для куба это тройное произведение длины его ребер. Ниже рассмотрим фигуру цилиндр и ответим на вопрос о том, как найти объем его.

Видео:Сколько в бочке литров? Посчитаем.Скачать

Понятие о цилиндре

Фигура, о которой пойдет речь, является достаточно непростой. Согласно геометрическому определению, она представляет собой поверхность, образованную путем параллельного перемещения прямой (генератрисы) вдоль некоторой кривой (директрисы). Генератриса также называется образующей, а директриса — направляющей.

Если директриса — это окружность, а генератриса перпендикулярна ей, тогда полученный цилиндр называют круглым и прямым. О нем и пойдет дальше речь.

Цилиндр имеет два основания, которые параллельны друг другу и соединены цилиндрической поверхностью. Проходящая через центры двух оснований прямая называется осью круглого цилиндра. Все точки фигуры находятся на одинаковом расстоянии от этой прямой, которое равно радиусу основания.

Круглый прямой цилиндр однозначно определяется двумя параметрами: радиусом основания (R) и расстоянием между основаниями — высота H.

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Формула объема цилиндра

Для расчета области пространства, которую занимает цилиндр, достаточно знать его высоту H и радиус основания R. Искомое равенство в этом случае имеет вид:

Понять эту формулу объема просто: поскольку высота перпендикулярна основаниям, то если ее умножить на площадь одного из них, получается нужная величина V.

Видео:Объем цилиндра.Скачать

Вычисление объема бочки

Для примера решим такую задачу: определим, сколько воды поместится в бочку, имеющую диаметр дна 50 см и высоту 1 метр.

Радиус бочки равен R=D/2=50/2=25 см. Подставляем данные в формулу, получаем:

V = pi*R2*H = 3,1416*252*100 = 196350 см3

Поскольку 1 л = 1 дм3 = 1000 см3, то получаем:

V = 196350/1000 = 196,35 литра.

То есть в бочку можно налить почти 200 литров воды.

Видео:Объём цилиндраСкачать

Формулы, позволяющие находить объём цилиндра в метрах и литрах

Среди множества геометрических фигур часто встречается и цилиндр. Это геометрическое тело применяется в многочисленных расчётах. Согласно принятой терминологии под таким понятием принято иметь ввиду тело геометрического типа, которое в своей основе имеет поверхность. Данная поверхность представляет также цилиндрическую форму.

В литературе данная поверхность часто именуется, как поверхность бокового вида. Кроме этого, в такой фигуре есть пара поверхностей, носящих наименование оснований. Эти основания цилиндра представляют собой окружности равного диаметра. Цилиндр, в основании которого находится круг принято считать круговым.

Ещё со школьных времён знакома всем фигура цилиндра классического типа. Это и есть круговой цилиндр.

Видео:Объем цилиндраСкачать

Типы цилиндров

В математике существует несколько типов цилиндров, которые постоянно используются в геометрии.

1. Цилиндр прямого типа. Это геометрическая фигура, которая имеет прямой угол между боковой поверхностью и основаниями. Такой тип самый распространённый и часто применяется в решении большого количества задач.
2. Наклонный цилиндр. Исходя из основания фигуры, можно сделать вывод, что угол между боковой поверхностью и основаниями фигуры будет отличным от прямого. При этом он может колебаться в своём значении, как в большую, так и в меньшую сторону от прямого угла.

Читайте также: Ремкомплект главного цилиндра сцепления краз 6510

Видео:Объём цилиндра измерили с помощью мензурки (см. рисунок). Масса цилиндра равна 320 г. - №27231Скачать

Вычисление объёма

Довольно часто для работы с цилиндрами требуется вычислить его объём. Это процедура в последнее время производится с применением вычислительной техники. Однако, чтобы провести такую процедуру необязательно использовать калькулятор и другие дополнительные методы решения поставленной задачи.

Сейчас существует несколько основных методов, которые позволяют произвести вычисление данного параметра. Это, по сути, универсальные формулы. Каждая из таких формул имеет свои входные параметры, отталкиваясь от которых и можно найти требуемое значение объёма. Это позволяет достигнуть ряда положительных моментов в расчётах.

1. Значительно сокращается время для осуществления операций подсчёта объёма.
2. Уменьшается вероятность того что может быть совершена ошибка в расчётах
3. Требуется для вычисления ограниченное число параметров, знание которых и даёт возможность достигать результата.

Видео:Видеоурок по математике "Цилиндр"Скачать

Исходные данные

Производя вычисление такого параметра, как объём, необходимо помнить, что требуется первоначальное знание параметра, который и будет исходным данным для такой процедуры.

Необходимо иметь значение высоты. Это расстояние от нижнего и верхнего основания фигуры. При этом в зависимости от типа она может определяться по-разному. В ситуации прямоугольного цилиндра высота соответствует расстоянию между основаниями фигуры. Если же он относится к наклонному типу, то расстояние будет вычисляться иным путём. Это параметр, который соответствует длине прямой проведённой под прямым углом от одного основания до плоскости, на которой лежит второе основание.

После определения такого значения можно приступать к вычислению объёма.

Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Методы расчёта

Существует два основных метода, которые позволяют производить вычисление такого параметра.

1. Метод вычисления объёма цилиндра на основе высоты геометрической фигуры. Этот метод является универсальным средством и может быть использован для фигур любого типа как прямоугольных, так и наклонных цилиндров. Дополнительно к значению высоты в данном способе следует знать и площадь основания. Если остановиться подробнее на данном параметре, то надо отметить что основанием является круг. Поэтому вычисление площади круга происходит на основе радиуса. Таким образом, вторым параметром в данном методе должен выступать радиус основания цилиндра. Тогда площадь определяется согласно стандартной формуле.

В данной формуле принято следующее обозначение при помощи переменных:

• П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
• R – Радиус окружности, лежащий в основании цилиндра.
• S — Площадь основания фигуры.

Вычисление непосредственно объёма цилиндра производится на основе стандартной формулы.

В данной формуле принято следующее обозначение при помощи переменных:

• S – Площадь основания цилиндра, имеющего форму круга.
• h – Высота геометрической фигуры.
• V – объём цилиндра.

1. Вторым методом, позволяющим произвести вычисление объёма данной фигуры, является соотношение таких параметров, как высота цилиндра и радиуса его основания. По сути, данная формула является преобразованной формулой первого метода. В ней нет разделения на промежуточные этапы подсчёта параметров. Сразу же включены все математические операции.

Таким образом, в ней одновременно производится подсчёт площади круга и объёма цилиндра.

Приведём формулу расчёта объёма цилиндра для данного метода.

В данной формуле принято следующее обозначение при помощи переменных:

• П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
• R – Радиус окружности, лежащий в основании цилиндра.
• h – Высота геометрической фигуры.
• V – Объём цилиндра.

Читайте также: Цилиндр катится по цилиндрической поверхности

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Объём в литрах

Если говорить о нахождении объёма такой геометрической фигуры, то надо отметить что это задача не только для школьной программы. Используя приведенные ранее методы, есть возможность производить расчёты объёма ёмкости неизвестного типа.

К примеру, есть возможность вычислить объём ёмкости для полива на садовом участке. Однако есть и особенность при проведении подсчёта. Надо все значения подставлять в формулы в метрах. В результате проведения расчётом получается значение, которое будет измеряться в кубических метрах.

Однако, принято при расчётах поливных ёмкостей пользоваться измерениями в литрах. Для этого необходимо произвести пересчёт полученного значения объёма в литры. Это происходит на основе простого соотношения, где один кубический метр равняется 1000 литрам жидкости.

Если вычисления происходят в сантиметрах, то и результат будет в кубических сантиметрах. Тогда надо понимать, что между кубическими сантиметрами и литрами существует чёткое соотношение. Перевод происходит путём деления полученного значения объёма на 1000. После этого данные будут представлены в литрах.

Если необходимо первоначально перевести полученный в результате вычислений параметр из кубических сантиметров в кубические метры, то достаточно произвести операцию деления. Объём делится на 1000000. Это связано с тем, что кубический метр — это куб, у которого сторона равняется 100 сантиметрам. Поэтому объём в сантиметрах будет равен произведению 100*1000*100. Соответственно это будет 1000000 сантиметров кубических.

Видео:Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать

Видео

Посмотрите, как высчитать объем цилиндра и площадь его поверхности.

Видео:Объем цилиндра. Урок 13. Геометрия 11 классСкачать

Объем цилиндра

Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.
Если вам необходимо вычислить объем цилиндра, то прежде, чем начать его вычисление отставьте прочь калькуляторы и свои методы решения. Ведь теперь у вас есть более легкий способ решить такую задачу, а именно наш онлайн калькулятор, который сэкономит ваше время и лишит возможности ошибиться. Все что от вас требуется это ввести несколько значений. Причем мы предлагаем два способа решения с любым из неизвестных.
Первый способ наш онлайн калькулятор вычисляет по формуле: , а второй по формуле
Где S – это площадь основания, h – это высота цилиндра, число пи равное 3.14159, а r— это радиус цилиндра.

Смотрите также

Спасибо, очень полезным оказался

Спасибо, очень удобный калькулятор. Вспомнила формулу вычисления объёма. Невозможно держать в голове всю школьную программу. Пользуешься только необходимыми вычислениями, которые нужны для моей профессии.

А в каких единицах измерения, в бананах или коровах? Услугами данного калькулятора пользуются не профессора! Бесполезно потраченное время!

Оксана, результат у тебя, и таких как ты, получится в кубических курах. Потому, что у вас мозги куриные!

В школу ходить надо было.
Если измерение проводится в см, то и получаете см возведённые в куб.

Учитель не до конца вам объяснил или вы не усвоили, что в геометрии как правило объем измеряется в кубах, соответственно:

— Если вводите в бананах, то результат будет в бананах кубических,
— Если в сантиметрах, то результат будет в сантиметрах кубических (см³).
и т.д.

Слушайте учителей, образовывайтесь, заставляйте свой мозг работать.

Не нужно быть профессором чтобы воспользоваться этим калькулятором
Разницы нету метры, сантимеры, миллиметры он вам выдаёт куб того что вы ввели.

📽️ Видео

Объём цилиндра измерили с помощью мензурки (см. рисунок). Масса цилиндра равна 320 г. Чему равна - №Скачать

Вычисление объёма цилиндраСкачать

Задачи на цилиндр. Объем цилиндра - bezbotvyСкачать

Как посчитать объем в м3 | Калькулятор для расчета объёма куба, параллелепипеда, шара, цилиндра.....Скачать