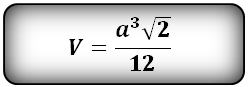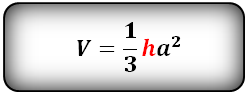- Как рассчитать, вычислить объём цилиндра? Что нужно для этого?
- Объем цилиндра
- Формула для вычисления объема усеченного цилиндра
- Объем цилиндра
- Объем правильного цилиндра через радиус и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
- Объем цилиндрической полости
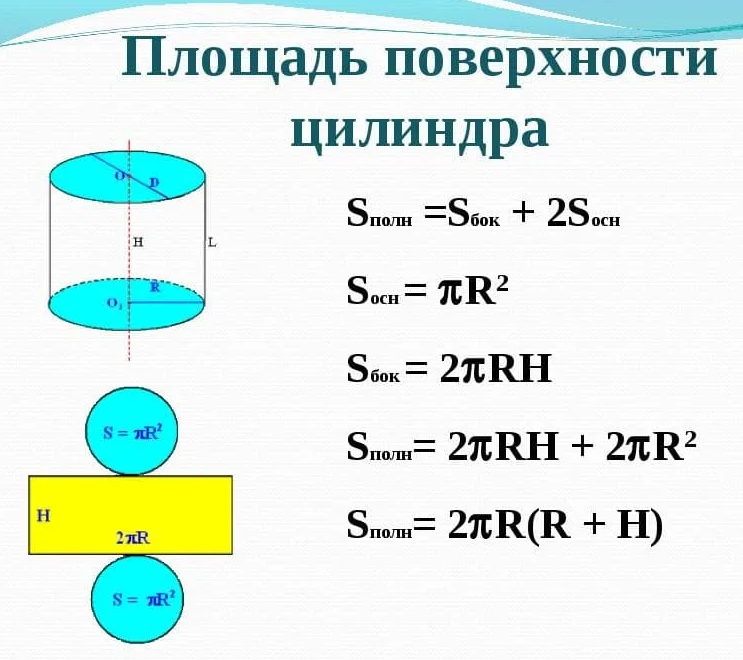
- Поверхности цилиндра
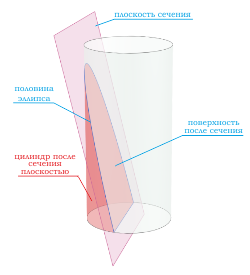
- Сечения цилиндра
- Что такое объем
- Калькулятор развертки усеченного плоскостью цилиндра онлайн
- Обозначения
- Введите радиус или диаметр *:
- Введите высоты * и (или) угол:
- Округление:
- Построение развёртки:
- Графики
- Формулы
- Калькулятор объема цилиндра в м3
- Объем цилиндра по высоте и радиусу
- Объём цилиндра через площадь основания и высоту
- Где применяется программа
- Все формулы объемов геометрических тел
- 1. Расчет объема куба
- 2. Найти по формуле, объем прямоугольного параллелепипеда
- 3. Формула для вычисления объема шара, сферы
- 4. Как вычислить объем цилиндра ?
- 5. Как найти объем конуса ?
- 7. Формула объема усеченного конуса
- 8. Объем правильного тетраэдра
- 9. Объем правильной четырехугольной пирамиды
- 10. Объем правильной треугольной пирамиды
- 11. Найти объем правильной пирамиды
Видео:Цилиндр - расчёт площади, объёма.Скачать

Как рассчитать, вычислить объём цилиндра? Что нужно для этого?
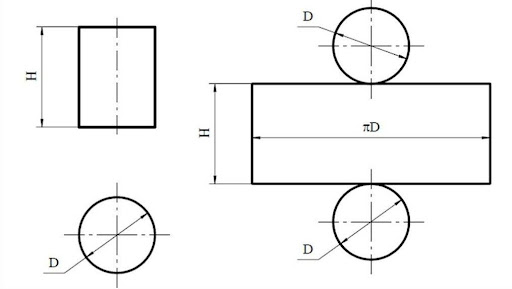
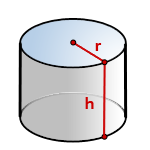
Цилиндром называется геометрическое тело, образованное путем вращения прямоугольника вокруг его стороны (преимущественно большей). Круги, лежащие в основании, конгруэнтные – соразмерные, равные.
Поверхность тела имеет криволинейную форму – цилиндрическую. Рассмотрим, как рассчитать объем цилиндра: полного и усеченного при наличии разных исходных данных. Развертка геометрического тела представлена:
- прямоугольником с шириной, равной высоте геометрического тела (H);
- длиной, равной образующей или радиусу нижней поверхности: c = πD = 2πr.
Видео:Объём цилиндраСкачать

Объем цилиндра
Объемом называется характеристика ограниченного геометрическим телом пространства. Показывает, сколько места занимает тело или сколько жидкости внутрь него можно залить. Близкие по значению слова – емкость, вместимость.
Существует несколько формул, позволяющих найти объем цилиндра; какая подойдет, зависит от исходной информации.
- π – число «Пи», равное приблизительно 3,1415;
- r – радиус круга;
- h – высота призмы или длина стороны прямоугольника, вокруг которой он вращался для образования цилиндра.
V=\pi \frac или \frac \pi d^2h, где:
- d – диаметр геометрического тела.
Рассмотрим, как вычислить объем цилиндра на практике, если известны его:
- радиус: r = 5 см;
- высота: h = 13 см.
Подставляем значения в формулу:
V = π * 5 2 * 13 = π * 25 * 13 = 325 π.
Если нужно реальное число, вместо π в формулу подставим его округленное значение 3,1415.
V = 325 * 3,1415 ≈ 1020,98 ≈ 1021 см 3 .
В случае, когда дан диаметр круга, его придется разделить на два для получения радиуса: r= \frac d или разделить на четыре после поднесения к квадрату; r= (\frac d) =\frac d^2.
Видео:Объем цилиндра.Скачать

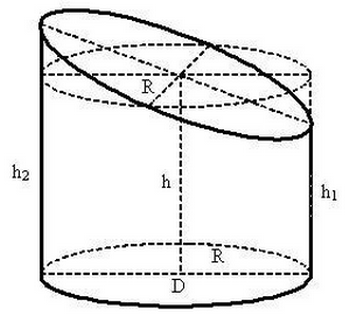
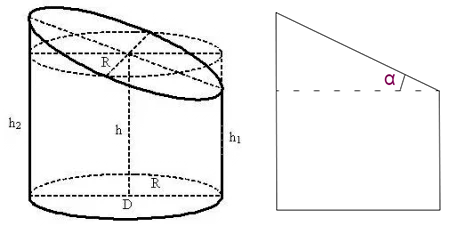
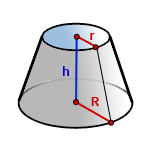
Формула для вычисления объема усеченного цилиндра
Усеченным называется цилиндр, часть которого отрезана плоскостью, пролегающей не параллельно нижней плоскости.
Формула объема усеченного цилиндра следующая:
здесь h1 b h2 – наименьшая и наибольшая высоты геометрического тела.
После подстановки значений получится выражение:
Первый: воспользуемся формулой V= \pi r^2 *\frac . Для этого определим радиус нижней плоскости.
r = \frac d= \frac 10=5 см.
V=\pi r^2 *\frac = \pi *5^2* \frac = 25 \pi * 20 = 500 \pi \approx 1570,75 см 3 .
Второе решение – подставим диаметр в формулу:
V = \pi \frac * \frac = \pi *\frac * \frac = \pi * \frac * \frac = 500 \pi \approx 1570,75 см 3 .
Зная высоту и радиус или диаметр основания тела, его вместительность высчитывается в несколько действий.
Читайте также: Объем жидкости в цилиндре правильный ответ
Видео:11 класс. Геометрия. Объем цилиндраСкачать

Объем цилиндра
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
Видео:Объем конуса. Объем усеченного конуса.Скачать

Объем правильного цилиндра через радиус и высоту цилиндра
Видео:Усеченный конус. 11 класс.Скачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
Видео:Объем цилиндраСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
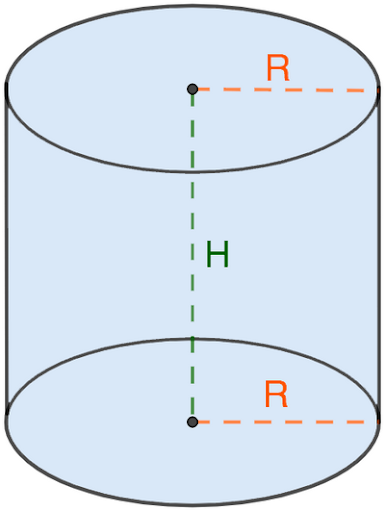
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Видео:Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать

Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Видео:Объем усеченного конуса. Практическая часть. 11 класс.Скачать

Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .
Видео:Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .
Читайте также: Цилиндры конусы призмы пирамиды
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Видео:Объем усеченного конуса. Практическая часть. 11 класс.Скачать

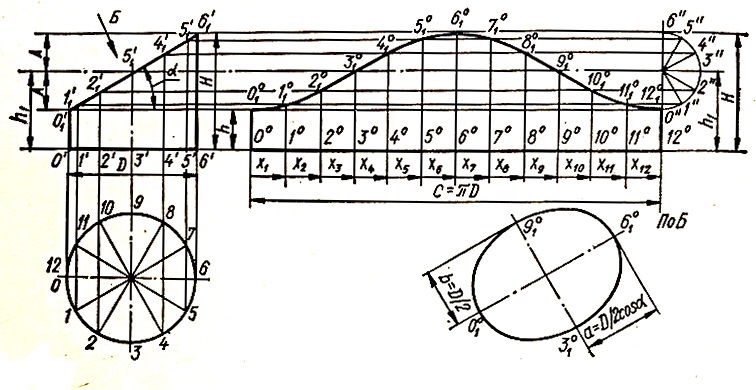
Калькулятор развертки усеченного плоскостью цилиндра онлайн
Видео:11 класс, 32 урок, Объем цилиндраСкачать

Обозначения
- R — радиус основания цилиндра;
- D — диаметр основания цилиндра;
- h — средняя высота усечённого цилиндра;
- h1 — наименьшая высота усечённого цилиндра;
- h2 — наибольшая высота усечённого цилиндра;
- α — угол сечения, град.
- X1 .. n — координаты для построения развёртки по оси X;
- Y1 .. n — координаты для построения развёртки по оси Y;
Числовые значения в таблице заполняются числом (5; 5.16; -3.12), либо математическим выражением (5/7; (1-5)*2.13)
Введите радиус или диаметр *:
Введите высоты * и (или) угол:
Без макс. и мин. высоты можно посчитать только площади боковой поверхности и основания и объём
Или введите одну из высот и угол сечения (рис.)
Округление:
Построение развёртки:
Видео:Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать
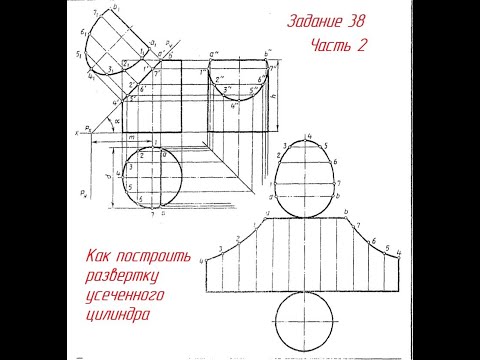
Графики
Чертится развертка усеченного плоскостью цилиндра, как показано на рисунке:
Видео:Как найти объем вписанного конуса? 🔍 #умскул_профильнаяматематика #умскул #никитасалливанСкачать

Формулы
Формула для вычисления значений Y:
Yi = D * tg(α) * sin (i * (180 / n)) , здесь: i — номер точки, α — угол сечения, n — количество точек развертки, D — диаметр цилиндра;
Формула для вычисления значений X:
Xi = ((π * R 2 ) / n) * i , здесь: i — номер точки, α — угол сечения, n — количество точек развертки, R — радиус цилиндра, π — число Пи (прим. 3.14);
Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Калькулятор объема цилиндра в м3
Цилиндр – это объемное тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают. Цилиндр (от греческого «kulindros» — ролик, каток) относится к основным геометрическим фигурам. В элементарных математических трактовках, он определяется как трехмерное тело. Объем цилиндра – один из базовых параметров, который необходимо уметь вычислять каждому человеку. Формула применяется во многих сферах промышленности, а также в строительстве, архитектуре, механике, программировании.
Видео:Объем цилиндра.Скачать

Объем цилиндра по высоте и радиусу
Узнать объем полой фигуры можно моментально, воспользовавшись удобной онлайн-программой. Сервис позволяет за секунды вычислить параметры тела и получить результаты в кубических сантиметрах, метрах, литрах. Расчет производится по двум математическим формулам:
- По высоте и радиусу: V = S х h.
Где V — объем, S — площадь, h — высота. Чтобы рассчитать объем необходимо площадь основания тела умножить на h. Следовательно, для этого необходимо знать две переменные.
Объём по площади основания и высоте: V = ∏ х R 2 х h
R – радиус, возведенный в квадрат. От первой формулы, расчет отличается тем, что сначала необходимо найти значение радиуса. Для этого диаметр делится на 2 или применяется формула S/2 х ∏ х H. ∏ — константа 3,14 (отношение длины окружности к диаметру).
Видео:Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать

Объём цилиндра через площадь основания и высоту
Программа позволяет определить объем тела по обеим формулам. Для этого необходимо только подставить цифры в соответствующие строки и нажать кнопку рассчитать. Пошаговая инструкция вычисления базовых показателей фигуры на калькуляторе по высоте и радиусу:
- в графе «h» ввести длину заданной фигуры, рядом выбрать метрику – в миллиметрах, сантиметрах, метрах;
- в строке «r» ввести радиус тела и выбрать меру длины (мм, см, м);
- в графе «Результат» определить, в чем будет выведен V – кубах, литрах.
Читайте также: Пропуски воспламенения в 4 цилиндре ваз 2115 причины
Например, длина фигуры составляет 1,6 метра, радиус 25 сантиметров. Объем равен 314.2 литров, 314200 куб. см или 0.314 куб. м. Результат выводится моментально, с точностью до тысячной. Правильность вычисления зависит только от достоверности исходных данных.
Где применяется программа
Сервис разработана для всех пользователей, чья профессиональная деятельность предполагает решение математических задач. Калькулятор будет полезен школьникам 5-9 классов, учащимся 11 классов в подготовительном процессе к ЕГЭ и контрольным срезам, а также родителям для проверки правильности решения задач.
С помощью сервиса можно решить типичные тестовые задания школьной программы, подставляя известные значения и не забывая выставлять метрические параметры (в кубических сантиметрах, кубометрах, миллиметрах, литрах). Например:
- Дан цилиндр, с площадью основания 58,3 см 2 и высотой 7 см. Чтобы посчитать V следует воспользоваться расчетом через площадь и высоту.
Решение: V = 58,3 см 2 х 7 см = 408.1 см³ или 0.408 л.
Вычисление: перед использованием программы следует определить радиус основания – 16см/2 = 8 см. Затем значения подставить в нужные поля. Расчет производится на основании формулы V = 3,14 х 8 2 х 11 см = 2211.968 см³.
Следует учитывать, что параметры полого горизонтального, наклонного, косого, кругового, равностороннего цилиндров вычисляются с использованием дополнительных формул.
Видео:Видеоурок по математике "Цилиндр"Скачать

Все формулы объемов геометрических тел
Видео:Объём цилиндраСкачать

1. Расчет объема куба
a — сторона куба
Формула объема куба, (V):
2. Найти по формуле, объем прямоугольного параллелепипеда
a , b , c — стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
3. Формула для вычисления объема шара, сферы
R — радиус шара
По формуле, если дан радиус, можно найти объема шара, (V):
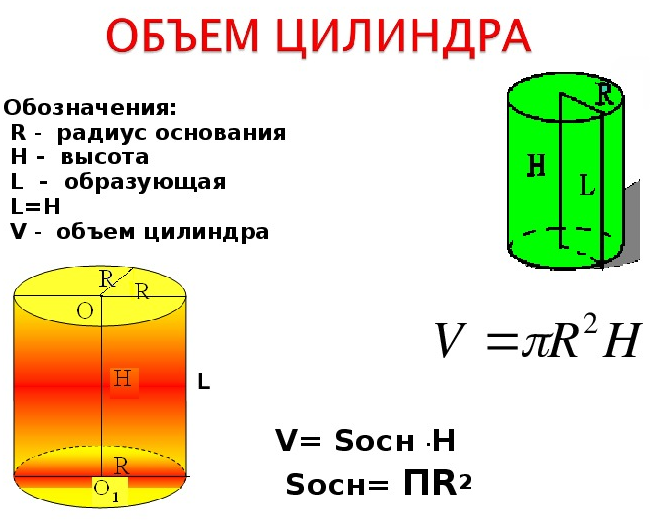
4. Как вычислить объем цилиндра ?
h — высота цилиндра
r — радиус основания
По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):
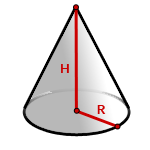
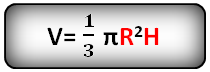
5. Как найти объем конуса ?
R — радиус основания
H — высота конуса
Формула объема конуса, если известны радиус и высота (V):
7. Формула объема усеченного конуса
r — радиус верхнего основания
R — радиус нижнего основания
h — высота конуса
Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
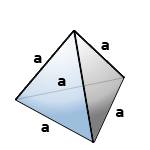
8. Объем правильного тетраэдра
Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.
а — ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
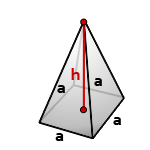
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
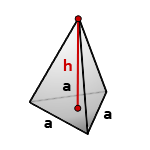
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):
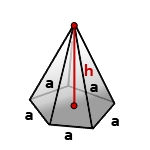
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h — высота пирамиды
a — сторона основания пирамиды
n — количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):