Как построить проекцию точек в цилиндре

Видео:ЦИЛИНДР. Проекции точек на его поверхности. Достроить недостающие проекции точек на трех плоскостяхСкачать

Построение проекций точек, принадлежащих цилиндру и конусу

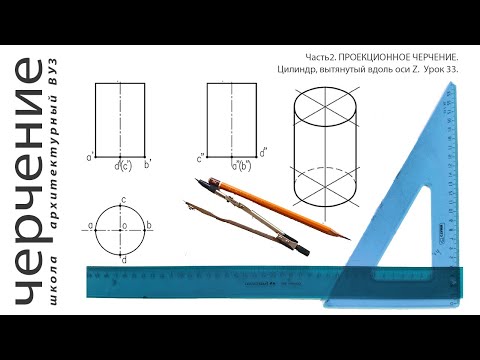
Пусть задана фронтальная проекция F₂ точки F, принадлежащей боковой поверхности цилиндра вращения (рис. 164, а). Требуется построить три проекции точки F. Как известно, цилиндр вращения образуется путем вращения прямоугольника вокруг одной из его сторон, принимаемой за ось вращения. Противоположная сторона прямоугольника (образующая или производящая) образует при вращении боковую поверхность цилиндра; две другие стороны прямоугольника образуют верхнее и нижнее основания цилиндра, являющиеся кругами одного и того же диаметра.

Поверхность цилиндра является в данном случае горизонтально-проецирующей поверхностью; следовательно, горизонтальная проекция F₁ точки Р должна совпадать с горизонтальной проекцией боковой поверхности цилиндра (с окружностью).

Проекция F₂ изображена светлым кружком; значит, точка F принадлежит передней поверхности цилиндра и спроецируется на нижнюю половину окружности в точку F₁. Третью проекцию F₃ строим с помощью ординаты у, откладывая ее размер вправо от оси z₃.

При построении изометрического изображения удобно пользоваться видимым для нас верхним основанием цилиндра (рис. 164, б). Строим эллипс в плоскости х’О’у’, проводим касательные-к нему прямые— видимые образующие цилиндра — и нижний полуэллипс. Точку F’ находим с помощью координатной ломаной, что ясно из сравнения чертежей.

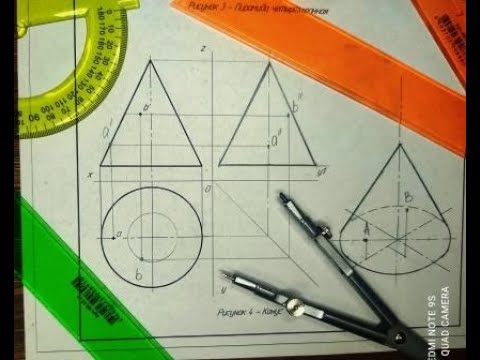
Пусть требуется построить три проекции точки G, принадлежащей поверхности конуса вращения (рис. 165, а).

Конус вращения образуется при вращении прямоугольного треугольника вокруг одного из его катетов. Гипотенуза прямоугольного треугольника является при этом образующей конуса. Верхняя точка образующей является вершиной конуса. Второй катет треугольника образует при вращении основание конуса. Судя по чертежу, вершина конуса расположена выше основания, поэтому вся боковая поверхность конуса будет видимой при проецировании на горизонтальную плоскость проекций П₁; при проецировании на фронтальную плоскость проекций П₂ видимой будет передняя половина боковой поверхности.

Фронтальная проекция G₂ задана светлым кружком, т. е. точка G принадлежит передней поверхности конуса. Для построения горизонтальной проекции G₁ существуют два способа: способ образующей и способ параллели. Рассмотрим способ образующей. Соединяем фронтальные проекции S₂ и G₂ прямой линией S₂H₂. Это будет фронтальная проекция образующей SH. Находим ее горизонтальную проекцию S₁H₁. Горизонтальную проекцию G_1. искомой точки G находим, проведя вертикальную линию связи G₂G₁. Этот способ не дает точного результата в тех случаях, когда точка лежит вблизи передней образующей конуса. Более универсальным является второй способ — способ параллели. Он заключается в проведении через точку G окружности или параллели а. Ее фронтальная проекция а₂ пересекает фронтальную проекцию левой образующей в точке А₂. Находим точку А₁ и радиусом А₁S₁ из центра S₁ проводим окружность а₁ — горизонтальную проекцию параллели а. Пересечение окружности с вертикальной линией связи определяет точку G₁. Третью проекцию G₃ находим с помощью ординаты у так же, как в предыдущей задаче; изображаем ее зачерненным кружком, поскольку точка G при проецировании на плоскость П₃ невидимая.

Видео:Построение проекций точек пересечения наклонного цилиндра прямой линиейСкачать

Черчение. 10 класс

Видео:Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

§ 16. Проекции точек на поверхностях геометрических тел

Проекции точек на поверхностях геометрических тел

Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.

Укажите количество вершин, ребер и граней изображенного предмета.

Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки.

Рассмотрим проекции точки на геометрических телах.

Проецирование точек на поверхности цилиндра

Последовательность проецирования точек
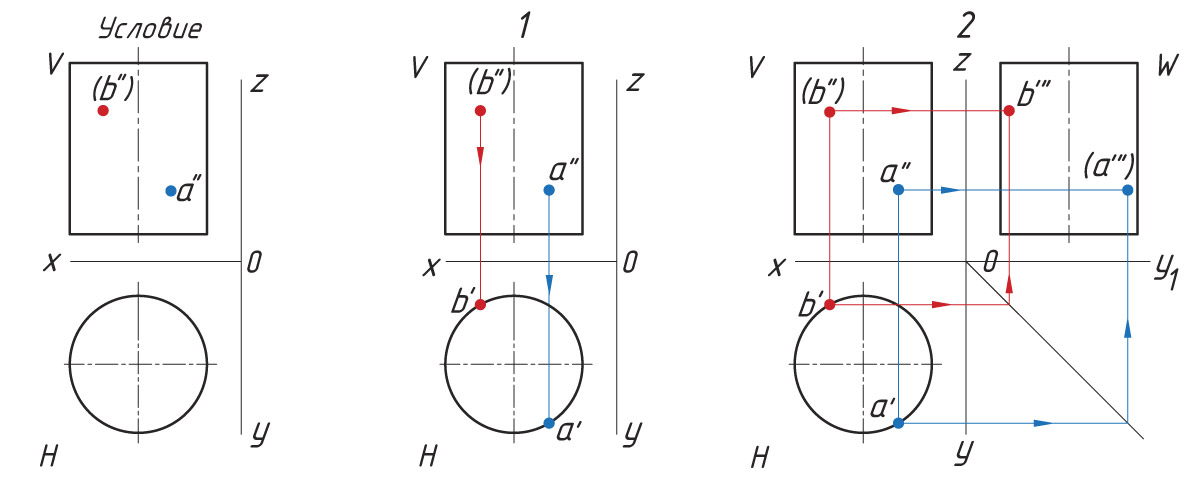
Заданы фронтальные проекции а″ и b″ точек А и В, лежащие на боковой поверхности цилиндра. Проекция а″ находится на видимой части поверхности цилиндра (на плоскости V показана без скобок), b″ находится на невидимой части поверхности цилиндра (на плоскости V показана в скобках).

1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью.

Читайте также: Как найти диагональ осевого сечения цилиндра формула

2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи.

Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).

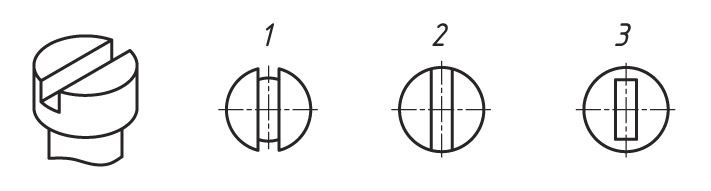
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.

Проецирование точек на поверхности призмы

Последовательность проецирования точек
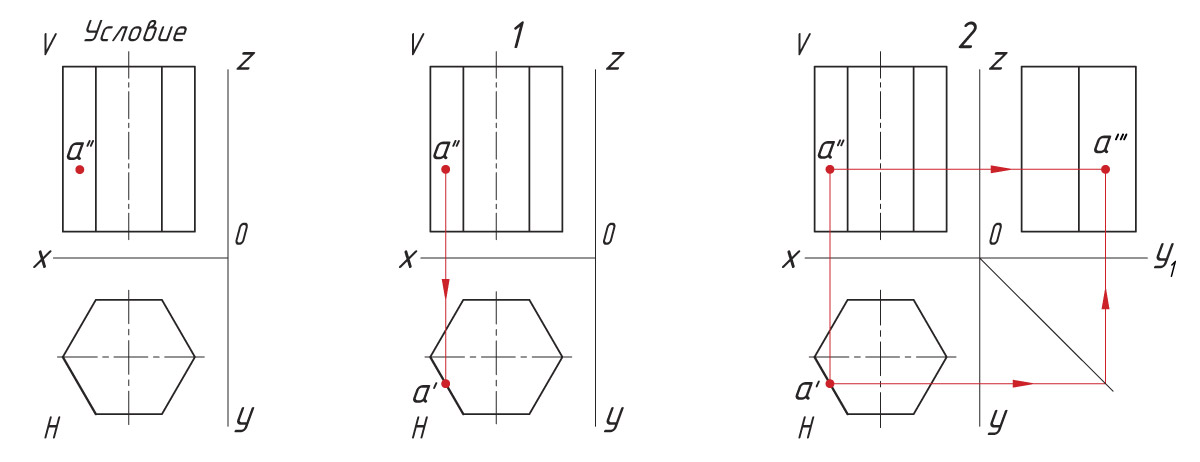
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности шестигранной призмы.

1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы).

2. Проекцию точки а′″ находят на пересечении линий проекционной связи.

Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.

Проецирование точек на поверхности пирамиды

Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.

Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.

Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.

Построение проекции точки, лежащей на грани
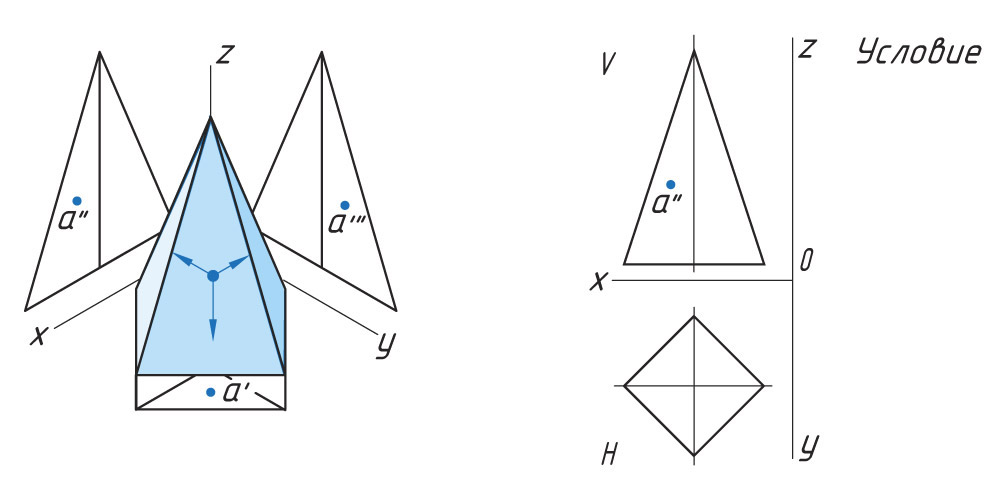
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.

Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.

1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″.
2. Проводят вертикальную линию связи из проекции f″ до пересечения с основанием на плоскости H в точке f′.
3. Точку f′ соединяют с вершиной пирамиды s′. На нее проводят вертикальную линию связи из проекции а″ до пересечения в точке а′.
4. Проекции точки а′″ находят на пересечении линий проекционной связи.

1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″.
2. Опустив из точки 1″ вертикальную линию связи до пересечения с соответствующим ребром на плоскости H, получают горизонтальную проекцию точки 1′.
3. Для нахождения проекции 2′ проводят из точки 1′ вспомогательную прямую, параллельную основанию до пересечения с ребром.
4. Горизонтальную проекцию а′ определяют, опустив вертикальную линию связи из точки а″ до пересечения со вспомогательной прямой 1′2′.
5. Проекцию точки а′″ находят на пересечении линий проекционной связи.

На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?

Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами.

Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А.
В способе II через точку А проводят вспомогательную плоскость, которая пересечет конус по окружности, расположенной в плоскости, параллельной основанию конуса.

Видео:Как начертить цилиндр в объемеСкачать

Как построить проекцию точек в цилиндре

Сечение цилиндра наклонной плоскостью

Этим уроком я открываю серию статей, посвященных построению линий пересечения простых тел вращения с наклонной плоскостью. Умение выполнять эти действия вам поможет не только решить одноименные задачи, но и будет серьезным подспорьем при нахождении натурального вида фигуры сечения сложных деталей. Ведь детали состоят из кусочков простых тел: конусов, цилиндров, параллелепипедов, сфер. Сегодня я научу вас строить линию пересечения плоскости с цилиндром. Исходное задание как правило имеет вид как на картинке слева от этого абзаца. Изображены два вида, дающие нам представление о том, что фигура является цилиндром вращения, а так же задается секущая плоскость, в моем случае это плоскость Pv.
Давайте попробуем предположить, что мы получим на каждом из трех видов? Определенно можно сказать, что вся линия пересечения на фронтальном виде сольется с прямой обозначающей секущую плоскость, а на горизонтальном виде, все точки пересечения будут лежать на окружности, которой задан цилиндр. Главный интерес данной задачи заключается в нахождении линии пересечения на третьем виде(на профильной проекции цилиндра). Вероятнее всего вы уже догадываетесь, что на третьем виде линия пересечения будет представлять собой эллипс. В частном случае, если секущая плоскость наклонена к цилиндру вращения под углом ровно 45 градусов, то в проекция сечения на третьем виде будет являться эллипсом с равными осями, т.е. эллипс выродится в окружность. Это был маленький кусочек теории, сейчас же предлагаю перейти к практическим построениям. Итак, перед нами цилиндр с заданной фронтально-проецирующей секущей плоскостью. Начнем с подготовки третьего вида. Он будет точно такой же как и главный вид:

Читайте также: Рулевые цилиндры газ 66

Первым делом давайте обозначим определяющие точки, которые можно найти сразу, без дополнительных построений. Определим точки 1′ и 2′. Горизонтальные проекции 1 и 2 лежат на пересечении образующей окружности с осью, а проекции 1» и 2» лежат на оси цилиндра. Это нужно либо понимать, либо поверить мне ?

Еще одна пара определяющих точек — точки 3 и 4. Определим их фронтальную проекцию, а потом найдем горизонтальную и профильную. Это не сложно:

Если бы наша задача была построить сечение в AutoCad, то на этом можно было бы остановиться, поскольку мы уже имеем 4 точки, определяющие оси эллипса. Но так как мы учимся чертить руками, то мы должны построить дополнительные точки, которые бы позволили нам с вами, не обладая точностью компьютера, максимально точно начертить линию пересечения.
Проведем вспомогательную секущую плоскость Q1. На фронтальной проекции в точке пересечения Q1 и Pv отметим точки 5′ и 6′. Снесем их по линии связи на горизонтальную проекцию, отметим там точки 5 и 6:

Теперь нужно построить профильные проекции 5» и 6». Отложим на фронтальной проекции влево от оси точку 6» на расстоянии равном удалению точки 6 от оси окружности на горизонтальной проекции. Эти соответствующие расстояния на рисунке ниже отмечены зелеными отрезками:

Чтобы построить точку 5» нужно выполнить ровно такие же действия. Нужно отложить аналогичное расстояние вправо от оси цилиндра. Соответствие размеров на профильной и горизонтальной проекции на рисунке ниже обозначено синими отрезками:

Проведем еще одну вспомогательную секущую плоскость — Q2. Мне нравится проводить вспомогательные плоскости симметрично относительно середины сечения — так во многих случаях удается сделать менее загруженный линиями чертеж. Т.е. я провел Q2 симметрично Q1 относительно точек 3′,4′. Полученные с ее помощью проекции точек 7 и 8 строим по аналогии с построениями проекций точек 5 и 6:

Мы ограничимся построением двух вспомогательных плоскостей и проведем эллипс по имеющимся точкам. Но на практике имеет смысл провести еще хотя бы по одной вспомогательной плоскости выше и ниже точки пересечения Pv с осью цилиндра. Особенно если вы не считаете себя мастером построения эллипса «от руки». Итак, завершающий этап: построение линии пересечения плоскости с цилиндром. Она имеет форму эллипса, строим его аккуратно соединяя точки. И последний штрих — на профильной проекции верхняя половина линии пересечения будет проходить за цилиндром, соответственно будет невидима. Что мы и обозначим штриховой линией.

В следующем уроке мы рассмотрим один из случаев построения линии пересечения конуса с плоскостью.

Вы можете сказать «спасибо!» автору статьи:

пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»

или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи

или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.

А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны:

Автор комментария: ирина
Дата: 2012-05-29

Автор комментария: Михаил
Дата: 2012-05-30

Мне нужно вырезать эллипс в крыше для вывода металлической трубы, поэтому мне важнее начертить проекцию цилиндра на самой крыше. Спасибо.

Читайте также: Площадь боковой поверхности цилиндра нельзя вычислить по формуле выберите

Михаил! Ваша задача сводится к продолжению задачи о сечении цилиндра плоскостью. Необходимо найти натуральную величину получившегося сечения. Имея его на руках — распечатываем на формате соответствующего размера, вырезаем трафарет и накладываем в нужном месте на крышу. Останется обвести и произвести вырезание по полученной линии. На сайте есть урок, связанный с нахождением натуральной величины сечений, но там не разобрано построение сечений циллиндрических поверхностей. Ну а в целом — спасибо за доброе слово!

Автор комментария: sakha
Дата: 2012-08-01

Вопрос к практическому применению, понятно как изготовить шаблон верхней проекции сечения, но мне, как сварщику, непонятно как изготовить шаблон для торцовки труб. Объясните, пожалуйста. Спасибо.
Сергей, попробую предложить вам способ. Сразу оговорюсь, что вряд ли он наиболее удобный, но зато качество разметки должно получиться хорошим. Метод потребует выполнить построение развертки цилиндра с нанесением на него линии пересечения с плоскостью. Т.е. я предлагаю вам на чем либо (рубероид, упаковочная бумага, лист обоев и т.д.) построить развертку цилиндра, нанести на нее линию пересечения цилиндра с наклонной плоскостью, отрезать лишнюю часть и, приложив ее к трубе, обвести по краю. Получиться должно просто замечательно.
Думаю, идею вы поняли. Ну а реализация построения линии пересечения на развертке цилиндра — либо найдете, либо дождетесь — планирую написать соответствующую статью.
Всего наилучшего!

Автор комментария: Игорь
Дата: 2012-10-09

Автор комментария:
Дата: 2013-12-17

Автор комментария: препод по ИГ
Дата: 2014-12-14

линия пунктир(пункт по немецки точка)не показывает невидимую линию. Линия невидимого контура называется штриховая. ГОСТ 2.303

Вот! Всегда есть шанс, что кто-то не поленится найти неточность и поправит! Спасибо за замечание, исправляю!

Автор комментария: Надежда
Дата: 2016-01-09

Автор комментария: дмитрий
Дата: 2016-04-18

Спасибо, это понятно по начерт.геометрии, но хотелось бы сделать построение математическим путём, т.к. шаблон, плаз, очень большой. Если дадите буду благодарен.

Автор комментария: vlad
Дата: 2016-04-25

спасибо огромноое очень помогло вспомнил

Автор комментария: Злой Енот
Дата: 2016-09-29

Извиняюсь, Вы нарисовали бред, попробуйте построить по Вашему методу сечение цилиндра плоскостью с наклоном 45 и получите круг, а не эллипс ))))

Приветствую Злого Енота! ? Зачем строить? Это и так известно, будет круг. У меня написано: эллипс с равными осями. Частный случай. Эллипс выродится в круг. Возможно, нужно было прочитать еще пару строк? Или попробовать построить эллипс с равными осями?

Автор комментария: Борис
Дата: 2017-09-17

спасибо очень пригодилось!

Автор комментария: Никита
Дата: 2017-10-29

Здравствуйте! Подскажите как выполните такое же задание при условии что цилиндр проецируется в виде круга на профильную плоскость? Зарание спасибо.

Автор комментария: Михаил
Дата: 2020-09-02

Благлдарю!Много перелопатил информации,и в основном построенной на рекламе,а толком ничего путного,все вокруг да около,а вот зашел на Ваш сайт,сразу все стало на свои места.Ведь я где-то далеко помню,это было еще в школьные годы,и кого не спрашивал,никто дать толковую информацию так и не смог.С помощью Ваших уроков я вышел из положения,и теперь рекомендую Ваш сайт своим друзьям,знакомым.Ведь много людей занимаются строительством,и часто и густо выходят из того или иного положения методом втыка.Благодарю еще раз.

Добавьте свой комментарий:

Не являюсь Вашим заказчиком, поскольку сам неплохо разбираюсь в предмете, да и принцип у меня есть — за весь период учебы не купил ни одной работы, всё делал сам. Кроме того, пока учился почти каждую ночь выполнял работы по НГ и ИГ. Я отошел от дел, так что рекламой этот пост не является ? Видимо я сильно продешевил в свое время, раз уж Ваши работы покупают за столь серьёзные по моим тогдашним меркам суммы. Залез к Вам на страницу, и кусаю локти теперь ? С уважением к Вам, коллеги Николай, ПГУПС

Николай, спасибо за ваше мнение! И я рад, что в результате нашей с вами переписки я получил эти строки: «Спасибо за реакцию, — признаться, приятно иметь дело с адекватным человеком. Надеюсь, не подпортил Вам репутации.»

💥 Видео

КОНУС. Проекции точек на его поверхности. Достроить недостающие проекции точек на трех плоскостях.Скачать

2 3 проекция точки на конусеСкачать

НАКЛОННЫЙ ЦИЛИНДР и недостающие проекции точек на его поверхности. Построить три проекции точек.Скачать

ПРОЕКЦИИ ТОЧЕК на поверхности шара (сферы). Построение трех проекций точек на заданной сфереСкачать

РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Построить проекции линии и точек на ней по заданным координатам. Начертательная геометрияСкачать

Проецирование точки на 3 плоскости проекцийСкачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Как начертить конус в объемеСкачать

Точка встречи прямой с поверхностью конусаСкачать

Построение проекций точек на поверхности конуса #черчение #проекции #конус #преподавательСкачать

Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Построение проекций точек на поверхности предметовСкачать