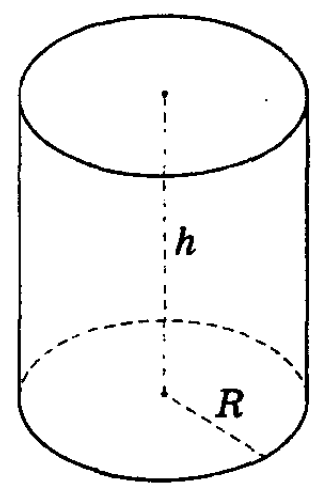
Как построить прямой круговой цилиндр (7 видео)

Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.

Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.

Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.

Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.

Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.

Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.

Круговой цилиндр — цилиндр, основания которого являются кругами.

Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.

Радиус цилиндра – радиус его основания.

Образующая цилиндра — образующая цилиндрической поверхности.

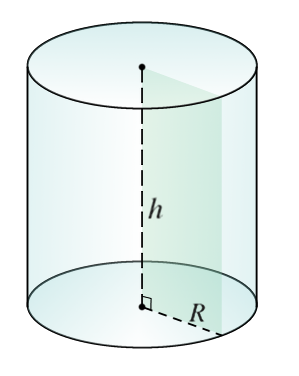
Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.

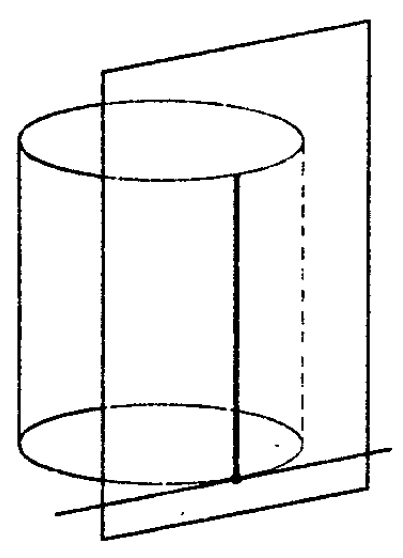
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.

Читайте также: Герметик для цилиндра бензопилы

Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.

Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_ =2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.

Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_ =2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.

Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).

Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.

Содержание

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Развертка прямого кругового цилиндра.
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
Развертка усеченного цилиндра.
🎬 Видео

Видео:Как начертить цилиндр в объемеСкачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.

Видео:Видеоурок по математике "Цилиндр"Скачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.

Развертка прямого кругового цилиндра.

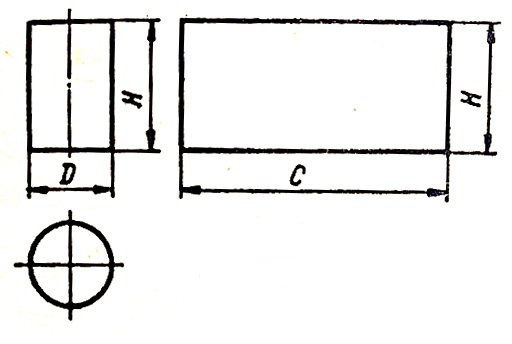
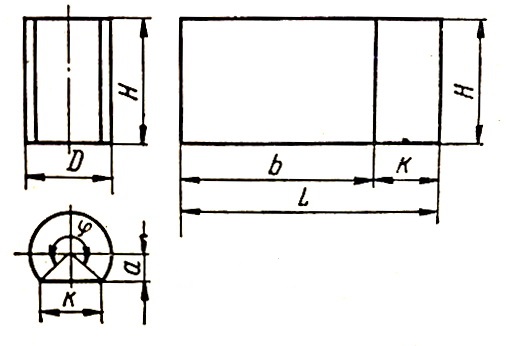
Цилиндр диаметром D и высотой H показан на рис. 1. Развертка представляет собой прямоугольник длиной с = πD и высотой Н.

Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2) 2 – a 2 ) = 2a tg (ᵠ/2).

Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.

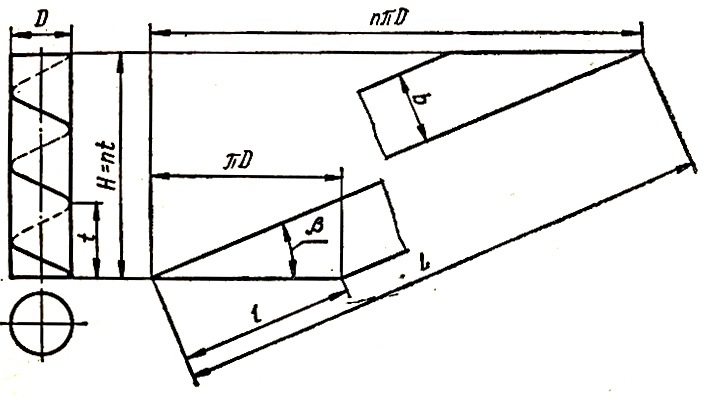
Цилиндр показан на рис. 3. При определении развертки можно использовать следующие зависимости:

n — число полных витков на общей длине цилиндра H, Н = nt;

Развертка усеченного цилиндра.

Для получения развертки горизонтальная проекция цилиндра делится на равные части и точки деления нумеруются (в данном случае от 0 до 12). Из точек деления проводятся вертикали до пересечения верхнего основания в точках 0′₁, 1′₁…, 6′₁. На продолжении прямой 0’6′ откладывается отрезок длиной с = πD, который делится на принятое число равных частей. Из точек деления 0₀, 1₀, …, 6₀ строятся перпендикуляры до их пересечения с соответствующими горизонтальными линиями в точках 0 0 ₁, 1 0 ₁, …, 6 0 ₁. Полученные точки соединяются плавной кривой. Ввиду симметричности остальные точки кривой находит аналогичным путем.

Читайте также: Что делать если маленькая компрессия во всех цилиндрах

Линию развертки можно определить и таким способом. На расстоянии h1 = (h + H)/2 от линии 0 0 12 0 проводится параллельная прямая. Из центра S, лежащего на прямой, описывается полуокружность радиусом А. Полуокружность делится на равные части, число которых равно половине точек деления развертки (в данном случае на шесть). Через точки деления 0ꞋꞋ, 1ꞋꞋ, …, 6ꞋꞋ проводятся горизонтальные прямые до пересечения вертикалей, проходящих через 0 0 , 1 0 , … , 12 0 . Полученные точки 0 0 ₁, 1 0 ₁, …, 12 0 ₁ соединяются плавной кривой.

Верхнее основание цилиндра представляет собой эллипс с полуосями a = D/2 cos α = 0′₁3′₁ и b = D/2.

При аналитическом определении координат точек кривой развертки цилиндра, усеченного плоскостью под углом α (рис. 5), могут быть использованы следующие зависимости:

x_k = kx₁ = πD/2 kε/180°; y_k = D/2 tg α sin kε = A sin kε = A sin ᵠ_i,

где х₁ = πD/ (2n) = πD/2 ε/180° — длина дуги окружности основания цилиндра, разделенная на 2n равных частей; ε = 360°/2n — центральный угол, соответствующий одному делению; k — порядковый номер точки; A = (H — h)/2 = (D/2) tg α — амплитуда синусоиды; ᵠ_i= kε.

Значения sin kε для наиболее часто употребляемых значений 2n приведены в табл. 1.

Таблица 1. Значения sin kε и sin 2 kε

2n				sin kε	sin 2 kε	2n				sin kε	sin 2 kε
8	16	32	64	sin kε	sin 2 kε	12	24	48	96	sin kε	sin 2 kε
—	—	—	1	0,09802	0,00961	—	—	—	1	0,06540	0,00428
—	—	1	2	0,19509	0,03806	—	—	1	2	0,13053	0,01704
—	—	—	3	0,29028	0,08426	—	—	—	3	0,19509	0,03806
—	1	2	4	0,38268	0,14645	—	1	2	4	0,25882	0,06699
—	—	—	5	0,47139	0,22221	—	—	—	5	0,32144	0,10332
—	—	3	6	0,55557	0,30866	—	—	3	6	0,38268	0,14645
—	—	—	7	0,63439	0,40245	—	—	—	7	0,44229	0,19562
1	2	4	8	0,70711	0,50000	1	2	4	8	0,50000	0,25000
—	—	—	9	0,77301	0,59754	—	—	—	9	0,55557	0,30866
—	—	5	10	0,83147	0,69134	—	—	5	10	0,60876	0,37059
—	—	—	11	0,88192	0,77778	—	—	—	11	0,65935	0,43474
—	3	6	12	0,92388	0,85355	—	3	6	12	0,70711	0,50000
—	—	—	13	0,95694	0,91573	—	—	—	13	0,75184	0,56526
—	—	7	14	0,98079	0,96194	—	—	7	14	0,79335	0,62941
—	—	—	15	0,99518	0,99039	—	—	—	15	0,83147	0,69134
2	4	8	16	1,00000	1,00000	2	4	8	16	0,86617	0,75000
—	—	—	17	0,89687	0,80438
—	—	9	18	0,92388	0,85355
—	—	—	19	0,94693	0,89668
—	5	10	20	0,96600	0,93301
—	—	—	21	0,98079	0,96194
—	—	11	22	0,99144	0,98296
—	—	—	23	0,99786	0,99572
3	6	12	24	1,00000	1,00000

Читайте также: Цилиндр 54 мм глухой 3012 54 dsa

Примечание: Значения sin kε и sin 2 kε даны для одной четверти окружности. В остальных четвертях они повторяются.

Ввиду симметричности синусоиды достаточно определить координаты точек одной четверти окружности, например от у₀ до у₃. Остальные координаты имеют соответственно равные значения. Например: у₄ — у₂, …, у₁₁ = — у₁ и т. д.