Как построить сечение цилиндра плоскостью параллельной его оси (8 видео)

Построение сечения прямого кругового цилиндра аналогично построению сечения призмы, так как прямой круговой нилиндр можно рассматривать как прямую призму с бесчисленным количеством ребер — образующих цилиндра. Выполнение чертежа начинают с построения трех проекций прямого кругового цилиндра. На поверхности цилиндра проводят несколько равномерно расположенных образующих, в данном примере двенадцать.

Для этого горизонтальную проекцию основания делят на 12 равных частей. С помощью линий связи проводят фронтальные проекции образующих цилиндра (рисунок 186). Из комплексного чертежа видно, что плоскость а» пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под углом к оси цилиндра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса (рисунок 186).

Фронтальная проекция фигуры сечения совпадает с фронтальным следом плоскости а». Горизонтальная проекция этой фигуры совпадает с горизонтальной проекцией основания цилиндра. Профильная проекция фигуры сечения представляет собой проекцию части эллипса и может быть построена но нескольким точкам, которые строятся с помощью линий связи по горизонтальной и фронтальной проекциям фигуры сечения. Полученные таким образом профильные проекции точек фигуры сечения соединяют кривой по лекалу.

Действительный вид фигуры сечения получен на рисунке 186 способом перемены плоскостей проекций.

Горизонтальная плоскость проекций заменена новой. Новая ось проекций гс2/л4 может быть проведена параллельно следу на произвольном расстоянии, но для упрощения построений она выполнена совпадающей с /о’а. От оси к2/п4 откладывают отрезки 5″5tv’-5’5x, 6″6’у-6’6Х, т. е. отрезки тип и т. д., так как расстояние от новой проекции этой точки до новой оси проекций равно расстоянию от прежней проекции этой точки до прежней оси проекций. Развертка боковой поверхности усеченного цилиндра с основанием и фигурой сечения показана на рисунке 187.

Возможно вам будут полезны данные страницы:

Для построения развертки на горизонтальной прямой откладывают длину окружности основания, равную тсс/, и делят се на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку nd, на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости а», которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки /0. 90, соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой /090 (сегмент), а фигуру нижнего основания цилиндра (окружность) соединяют с нижней частью развертки.

Читайте также: Порядок расположения цилиндров линкольн навигатор

Изометрическую проекцию усеченного

цилиндра строят следующим образом (рисунок 188). 7 Рисунок 188 в Сначала строят изометрию нижнею основания (эллипс) и части верхнею основания — сегмента (часть эллипса). На диаметре окружности нижнего основания от центра откладывают отрезки a, b и т. д., взятые с горизонтальной проекции основания (рисунок 186).

Затем из намеченных точек проводят прямые, параллельные оси цилиндра до пересечения с осью эллипса. Через полученные точки проводят прямые, параллельные оси у, и на них откладывают отрезки, взятые с действительного вида сечения. Полученные точки соединяют по лекалу. Заканчивают построение проведением очерковых образующих, касательных к основаниям эллипса.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Содержание

Как построить сечение цилиндра плоскостью параллельной его оси
Урок геометрии в 11-м классе на тему «Сечение цилиндра плоскостями»
Как построить сечение цилиндра плоскостью параллельной его оси
Как построить сечение цилиндра плоскостью параллельной его оси
📸 Видео

Видео:№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Как построить сечение цилиндра плоскостью параллельной его оси

Высота цилиндра равна 3, а радиус основания равен 13.

а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.

б) Найдите расстояние от плоскости сечения до центра основания цилиндра.

а) Пусть OO₁ — ось цилиндра. Проведем AB и CD параллельно оси цилиндра. Проведем BD и AC. Так как через две параллельные прямые проходит единственная плоскость, то прямоугольник BDCA — искомое сечение (см. рис.).

б) В этом прямоугольнике одна сторона будет равняться высоте цилиндра, а вторая — хорде окружности, лежащей в основании. Так как то где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора.

Таким образом, расстояние от центра окружности до сечения равно 5.

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Видео:Сечение цилиндра плоскостью, параллельной его осиСкачать

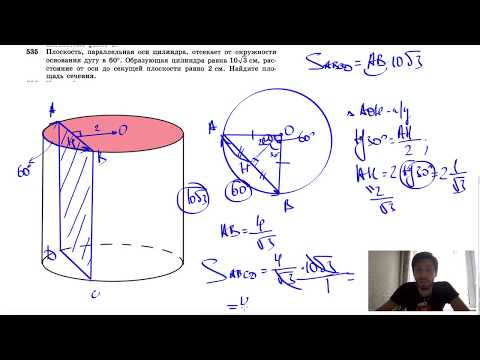
Урок геометрии в 11-м классе на тему «Сечение цилиндра плоскостями»

Цели и задачи урока:

Используя электронный учебник познакомить учащихся с сечением, рассмотреть виды сечений. Сформировать у учащихся умения и навыки построения сечения.
Развивать: образное мышление, память, речь.
Воспитывать: интерес к предмету, самостоятельность, аккуратность.

Оборудование: урок проходит в компьютерном классе, с использованием электронного учебника: Уроки геометрии Кирилла и Мефодия 2006г. 11 класс, карточки шаблоны (приложение4), карточки с задачами (приложение3)

Содержание урока:

Организационный момент (2-3 мин)
Повторение: (фронтальный опрос 5мин)
Объяснение нового материала: ввести понятие сечения, рассмотреть виды сечения (презентация в РР 10 мин) (приложение1)
С помощью электронного учебника сделать вывод (самостоятельная работа 10мин)
Работа с доской построение сечений: осевое, косое, параллельное его оси, перпендикулярное его оси и решение задач.(8мин)
Итог урока: тест (проверка знаний 5 мин) (приложение2)
Домашнее задание: п.53, з.3,4, Постройте сечение цилиндра имеющего форму квадрата. (2 мин)

1. Повторение: проверка усвоения материала

Вопросы:

Объясните что такое круговой цилиндр (образующая цилиндра, основания и боковая поверхность цилиндра)
Какой цилиндр называется прямым?
Что такое радиус цилиндра
Что такое высота цилиндра
Что такое ось цилиндра

2. Объяснение нового материала: ввести понятие сечения, рассмотреть виды сечения (презентация в РР 15 мин) (приложение1)
3. Электронный учебник: Уроки геометрии Кирилла и Мефодия 2006г

Расположение в электронном учебнике (адрес)

Выбор урока —> округлые тела —> цилиндр —> содержание урока —> 17,18,19,20.22,28,29,23,34,35.

4. С помощью электронного учебника сделать вывод (самостоятельная работа 10 мин)

Теорема: (о сечении цилиндра плоскостью, параллельной основаниям)

Сечение цилиндра плоскостью, параллельной основаниям, есть круг того же радиуса, что основания.

Теорема: (о сечении цилиндра плоскостью, перпендикулярной основаниям)

Сечение цилиндра плоскостью, проходящей через его ось или параллельной этой оси, есть прямоугольник.

Линия пересечения плоскости с цилиндрической поверхностью — это овал, полученный путем сжатия или растяжения окружности, в математике такая поверхность называется эллипсом. Эллипс имеет центр симметрии и две взаимно перпендикулярные оси симметрии. Отрезки этих осей симметрии, заключенные внутри эллипса, называются большой и малой осями эллипса.

5. Работа с доской построение сечений:

Осевое, косое, параллельное его оси, перпендикулярное его оси. (4 человека у доски строят сечения),
Остальные ребята строят на готовых шаблонах все четыре сечения. (приложение4)
Сильные ребята решают задачи (самостоятельно) на нахождения площади сечения (приложение3)

6. Итог урока: тест (проверка знаний 5 мин) (приложение2)

7. Домашнее задание: п.53, з.3,4, Творческое задание: постройте сечение цилиндра имеющего форму квадрата, как вы думаете, будет называться этот цилиндр?

Видео:№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать

Как построить сечение цилиндра плоскостью параллельной его оси

· рассмотреть основные виды сечений цилиндра

Время реализации занятия: 45 минут

II Проверка домашнего задания

III Изучение нового материала

Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 1, а). Две его стороны — образующие цилиндра, а две другие — параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это — сечение цилиндра плоскостью, проходящей через его ось (рис. 1, б).

Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

Пусть β — плоскость, параллельная плоскости основания цилиндра (рис. 2). Параллельный перенос в направлении оси цилиндра, совмещающий плоскость Р с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью Р с окружностью основания. Теорема доказана.

IV Закрепление изученного материала

Осевое сечение цилиндра — квадрат, площадь которого Q. Найдите площадь основания цилиндра.

Сторона квадрата равна IQ . Она равна диаметру основания. Поэтому площадь основания равна:

Видео:Построить сечение цилиндра с плоскостью общего положения.Скачать

Как построить сечение цилиндра плоскостью параллельной его оси

Диагональное сечение параллелепипеда – это сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Это сечение всегда представляет собой прямоугольник или квадрат.
Диагональное сечение разбивает параллелепипед на две призмы

Диагональным сечением пирамиды называется сечение её плоскостью, проходящей через два боковых ребра пирамиды, не лежащих в одной грани.
Это сечение всегда представляет собой треугольник.
Любое диагональное сечение разбивает пирамиду на две пирамиды..

Осевое сечение фигуры – это сечение, которое проходит через ось фигуры и перпендикулярно основанию.
Осевое сечение конуса – это всегда равнобедренный треугольник.

Осевое сечение усеченного конуса – равнобедренная трапеция

Осевое сечение цилиндра – прямоугольник. Любое сечение, параллельное осевому – тоже прямоугольник.

3. Сечения плоскостью, параллельной основанию

3.1. Сечение цилиндра плоскостью, параллельной его основаниям
Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

3.2. Сечение конуса плоскостью, параллельной его основанию
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковая поверхность – по окружности с центром на оси конуса.