Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Методические указания по решению задач в рабочей тетради
Загрузить всю книгу
Видео:Как начертить цилиндр в объемеСкачать

Модуль №1
Точка
Задача №1
Построить комплексные чертежи точек: А(15,30,0), В(30,25,15), С(30,10,15), D(15,30,20)
Решение задачи разделим на четыре этапа.
Как Вы думаете, если у точки А координата zA =0, то какое положение она занимает в пространстве?
Так выглядит комплексный чертеж точки А построенный по заданным координатам
Если у точки одна координата равна нулю, то точка принадлежит одной из плоскостей проекции. В данном случае у точки нет высоты: z = 0, следовательно точка А лежит в плоскости П1.
На комплексном чертеже оригинал (т.е. сама точка А) не изображается, есть только ее проекции.
На втором этапе объединим построение двух точек.
а) Координаты х точек одинаковы, следовательно, в системе П1 – П2 проекции точек лежат на одной линии связи (рис. 1.2),
б) Координаты z точек совпадают, (обе точки одинаково удалены от П1 на 15мм,) т.е. они расположены на одной высоте, следовательно на П2 проекции точек совпадают: В2= (С2).
в) Для определения видимости относительно П2 смотрим на рис. 1.3. Наблюдатель видит точку В, которая закрывает собой точку С, т.е. точка В расположена ближе к наблюдателю, поэтому на П2 она видима. (См. М1 — 13 и 16).
В системе П2П3 проекции точек также лежат на одной линии связи и видимость определяется по стрелке (рис. 1.2).
Точки В и С — называются фронтально конкурирующими.
а) На этом комплексном чертеже (рис. 1.4) построены три проекции точки D ( D 1, D 2, D 3).
Все три координаты имеют числовые значения, отличные от нуля, поэтому точка не принадлежит ни одной плоскости проекций.
б) Совместим пространственное изображение А и D (рис. 1.5). В системе П1-П2 проекции точек А и D лежат на одной линии связи, только точка D выше точки А, следовательно D — видима, а А — невидима (видима на П1 та точка, которая расположена выше)
Читайте также: Материалы при производстве гильз цилиндров
На четвертом, завершающем этапе, соединим все три фрагмента комплексных чертежей точек А,В,С, D в один общий.
Точки А и D — называются горизонтально конкурирующими.
Видео:Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
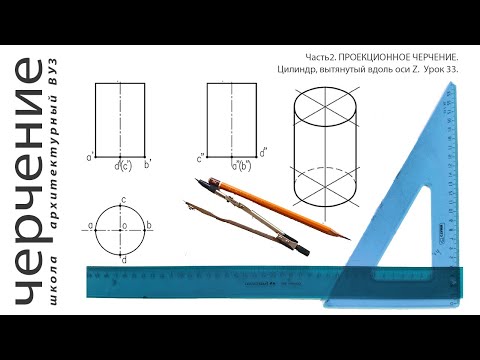
Построение проекций точек, принадлежащих цилиндру и конусу
Пусть задана фронтальная проекция F2 точки F, принадлежащей боковой поверхности цилиндра вращения (рис. 164, а). Требуется построить три проекции точки F. Как известно, цилиндр вращения образуется путем вращения прямоугольника вокруг одной из его сторон, принимаемой за ось вращения. Противоположная сторона прямоугольника (образующая или производящая) образует при вращении боковую поверхность цилиндра; две другие стороны прямоугольника образуют верхнее и нижнее основания цилиндра, являющиеся кругами одного и того же диаметра.
Поверхность цилиндра является в данном случае горизонтально-проецирующей поверхностью; следовательно, горизонтальная проекция F1 точки Р должна совпадать с горизонтальной проекцией боковой поверхности цилиндра (с окружностью).
Проекция F2 изображена светлым кружком; значит, точка F принадлежит передней поверхности цилиндра и спроецируется на нижнюю половину окружности в точку F1. Третью проекцию F3 строим с помощью ординаты у, откладывая ее размер вправо от оси z3.
При построении изометрического изображения удобно пользоваться видимым для нас верхним основанием цилиндра (рис. 164, б). Строим эллипс в плоскости х’О’у’, проводим касательные-к нему прямые— видимые образующие цилиндра — и нижний полуэллипс. Точку F’ находим с помощью координатной ломаной, что ясно из сравнения чертежей.
Пусть требуется построить три проекции точки G, принадлежащей поверхности конуса вращения (рис. 165, а).
Конус вращения образуется при вращении прямоугольного треугольника вокруг одного из его катетов. Гипотенуза прямоугольного треугольника является при этом образующей конуса. Верхняя точка образующей является вершиной конуса. Второй катет треугольника образует при вращении основание конуса. Судя по чертежу, вершина конуса расположена выше основания, поэтому вся боковая поверхность конуса будет видимой при проецировании на горизонтальную плоскость проекций П1; при проецировании на фронтальную плоскость проекций П2 видимой будет передняя половина боковой поверхности.
Читайте также: Цилиндр тормозной передний левый калина 1117
Фронтальная проекция G2 задана светлым кружком, т. е. точка G принадлежит передней поверхности конуса. Для построения горизонтальной проекции G1 существуют два способа: способ образующей и способ параллели. Рассмотрим способ образующей. Соединяем фронтальные проекции S2 и G2 прямой линией S2H2. Это будет фронтальная проекция образующей SH. Находим ее горизонтальную проекцию S1H1. Горизонтальную проекцию G1. искомой точки G находим, проведя вертикальную линию связи G2G1. Этот способ не дает точного результата в тех случаях, когда точка лежит вблизи передней образующей конуса. Более универсальным является второй способ — способ параллели. Он заключается в проведении через точку G окружности или параллели а. Ее фронтальная проекция а2 пересекает фронтальную проекцию левой образующей в точке А2. Находим точку А1 и радиусом А1S1 из центра S1 проводим окружность а1 — горизонтальную проекцию параллели а. Пересечение окружности с вертикальной линией связи определяет точку G1. Третью проекцию G3 находим с помощью ординаты у так же, как в предыдущей задаче; изображаем ее зачерненным кружком, поскольку точка G при проецировании на плоскость П3 невидимая.
Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Чертежик
Метки
Видео:Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

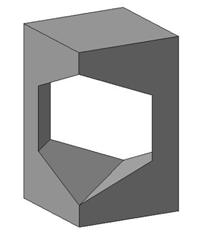
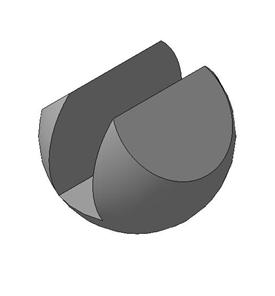
Построение фигуры-цилиндр с вырезом
Цилиндр с вырезом — распространенное задание для студентов. В образовательных учреждениях выдаются задания с разнообразными вырезами, но общий порядок построения не меняется.
Рассмотрим в качестве примера данное задание:
Необходимо построить фронтальный вид (вид слева) с существующим вырезом.
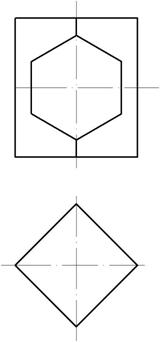
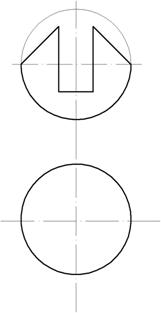
Построение фигуры-цилиндр с вырезом состоит из следующих шагов:
- Чертится цилиндр в трех видовых проекциях. На профильном виде указывается вырез.
- Вырез сквозной, соответственно на виде сверху строятся невидимые линии (невидно при визуальном просмотре сверху, но он есть).
- Методом вращения крайние точки переносятся на вид слева.
- Проводятся прямые от профильного вида и прямые от оси. В месте пересечения указываются точки. (для лучшего представления обозначены разными цветами)
- Обводятся контуры соответствующими линиями.
Рекомендую посмотреть видео по данной теме:
Видео:Построение цилиндра с вырезомСкачать

Построение вырезов на геометрических телах
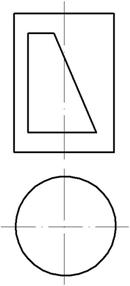
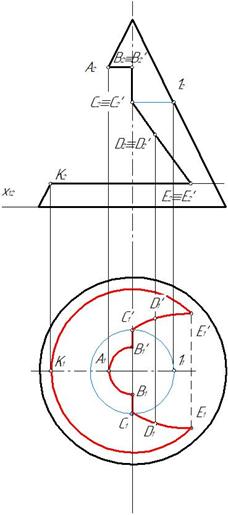
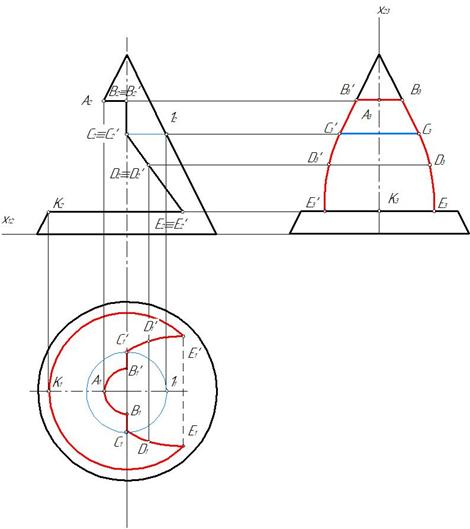
Пример 1. Построить три проекции цилиндра с вырезом (рис. 147).
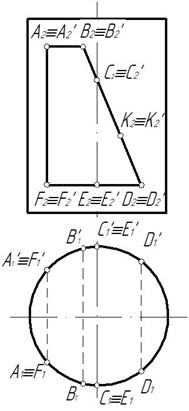
Отмечаем характерные точки выреза А, В, С, Д, Е, F, а также произвольную точку к для построения профильной проекции части эллипса. Горизонтальные проекции точек отмечаем на горизонтальном очерке цилиндра, так как горизонтальная проекция боковой поверхности цилиндра совпадает с горизонтальным очерком (рис .148)
Читайте также: Сыр цилиндр в вакууме
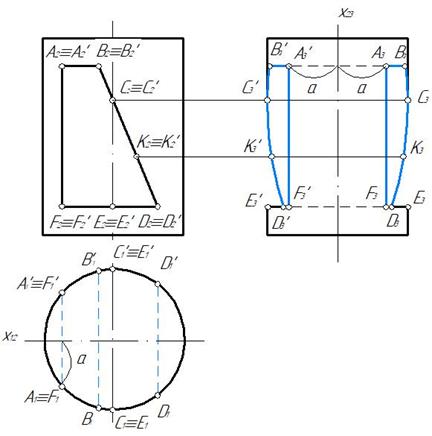
Построение профильной проекции выреза показано на рис. 149. Для этого целесообразно ось x 12 провести через ось симметрии горизонтальной проекции,а ось x 23 через профильную ось симметрии.
Пример 2. Построить три проекции конуса с вырезом (рис. 150).
Отмечаем характерные точки вареза А, В, С, Е, K, а также произвольную точку D для построения части эллипса. Горизонтальные проекции точек отмечаем на образующих конуса и вспомогательных окружностях (рис. 151).
На рис. 152 показано построение профильной проекции конуса с вырезом.Для этого целесообразно ось x 12 провести через ось симметрии горизонтальной проекции, а ось x 23 через профильную ось симметрии.
Пример 3. Построить три проекции вырезе на призме (рис. 153).
Решение показано на рис. 154
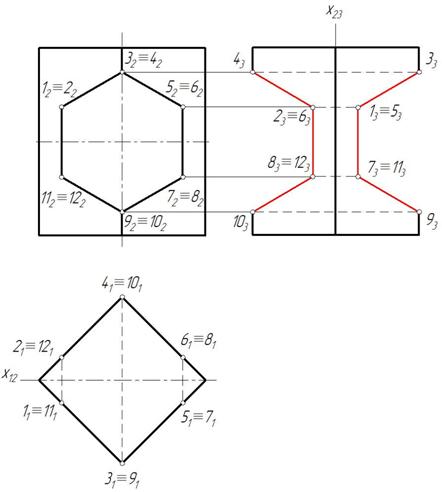
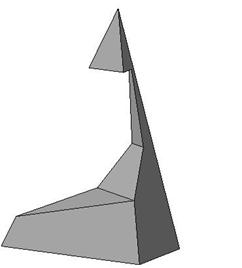
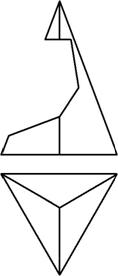
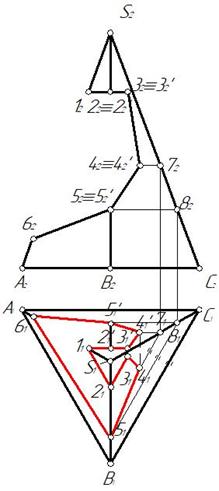
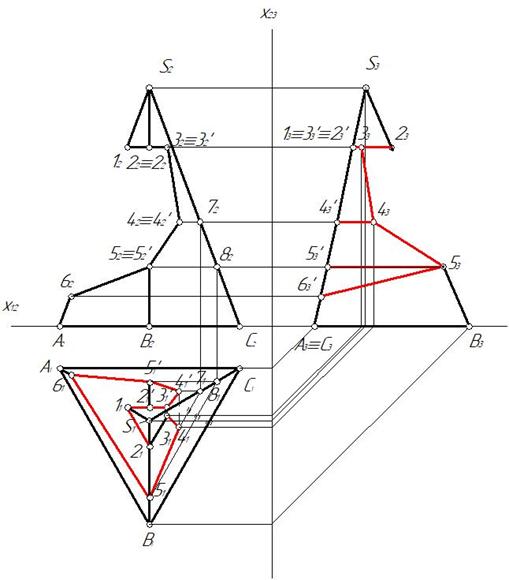
Пример 4. Построить три проекции выреза на пирамиде (рис. 155).
Отмечаем фронтальные проекции характерных точек выреза – это точки 12, 22, 32, 42, 52, 62. Для нахождения горизонтальных проекций точек 4 и 5 проводим по поверхности пирамиды две вспомогательные линии, параллельные основанию пирамиды ABC. Горизонтальные проекции этих линий являются треугольниками, параллельными горизонтальной проекции основания А1В1С1. На этих треугольниках отмечаем горизонтальные проекции точек 4 и 5 (рис. 156).
Затем строим профильную проекцию пирамиды и точек выреза. Для этого оси целесообразно провести как показано на рис. 157.
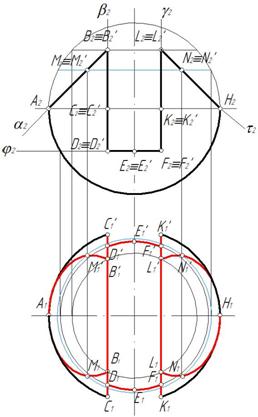
Пример 5. Построить три проекции выреза на сфере (рис. 158).
Вырез образован двумя фронтально-проецирующими плоскостями α и τ, горизонтальной плоскостью φ, двумя профильными плоскостями β и γ. Горизонтальная плоскость пересекает поверхность сферы по части окружности, ограниченной прямой. Фронтально-проецирующая плоскость пересекают поверхность сферы по окрухностям, которые на горизонтальной и профильной плоскости проецируются как части эллипсов. Профильная плоскость пересечет поверхность сферы по части окружности, которая на профильной плоскости спроецируется как часть окружности (рис. 159).
Построение профильной проекции показано на рис. 160
📸 Видео
ЦИЛИНДР. Проекции точек на его поверхности. Достроить недостающие проекции точек на трех плоскостяхСкачать

Построение цилиндра в трех проекциях и его прямоугольной диметрии.Скачать
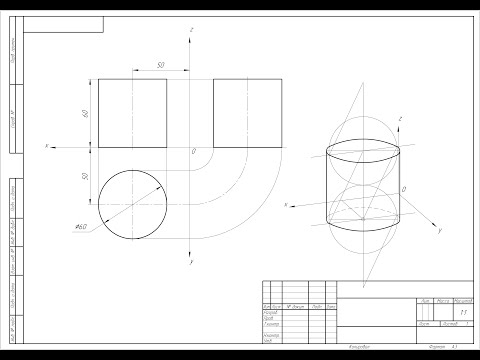
Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Цилиндр с вырезомСкачать

Изометрическая проекция цилиндра. Чертим вместе.Скачать

Вырез на цилиндре. Недостающие проекции выреза на теле вращения. Три проекции цилиндра с вырезом.Скачать

цилиндр полый с отверстием.Скачать

Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Изометрия цилиндраСкачать

Цилиндр 1 частьСкачать