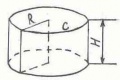
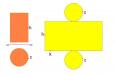
Поверхность цилиндра состоит из двух равных кругов радиуса R и прямоугольника, ширина которого равна высоте цилиндра, длина вычисляется по формуле С=2пR , где п=3,14. Изображение цилиндра и его развертка на рисунках:
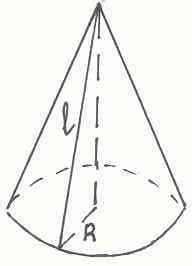
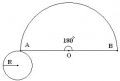
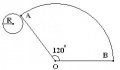
Поверхность конуса состоит круга радиуса R и сегмента круга радиуса OA. Дуга АВ=2пR. Изображение конуса и его разверток показаны на рисунках:
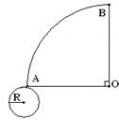
а) Когда угол прямой имеем четверть круга. Чтобы дуга АВ=2пR, надо чтобы АО=4R
б) Когда угол развернутый имеем половину круга. Чтобы дуга АВ=2пR, надо чтобы АО=2R
в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AB=2пR, надо чтобы АО=3R
Развертка «Усеченный конус»
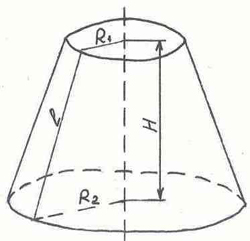
Поверхность усеченного конуса состоит двух кругов радиуса R1 , R2 и сегмента круга радиуса OA. Дуга AB=2пR. Изображение усеченного конуса и его разверток показаны на рисунках:
а) Когда угол прямой имеем четверть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=4R1, В1О=4R2
б) Когда угол развернутый имеем половину круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=2R1, В1О=2R2
в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=3R1, В1О=3R2
- Развертка цилиндра
- Развертка цилиндра для склеивания
- Круглый прямой цилиндр, развертка и формула для ее площади
- Цилиндр как фигура геометрии
- Круглый прямой цилиндр
- Развертка круглого прямого цилиндра
- Площадь развертки цилиндра
- Задача на нахождение радиуса фигуры
- Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
- Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
- Развертка прямого кругового цилиндра.
- Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
- Развертка усеченного цилиндра.
- 💥 Видео
Видео:Построение развертки цилиндра. Урок 37.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Развертка цилиндра
Для того, что-бы сразу получить готовую развертку цилиндра, кликните по ссылке.
Для получения готовой развертки наклонного цилиндра, кликните по этой ссылке.
Если нужна развертка конуса, то переходите сюда.
Для получения развертки усеченного конуса, переходите сюда..
Если же Вас интересует вопрос, как сделать развертку цилиндра самостоятельно, без использования калькулятора разверток, то следующая статья для Вас.
Видео:Построение развёртки усечённого цилиндра.Скачать

Развертка цилиндра для склеивания
Цилиндр — простая геометрическая фигура, представляющая из себя вытянутое тело, ограниченное с обоих сторон двумя плоскостями (основаниями).
Для простоты представления, прямая труба — это цилиндр.
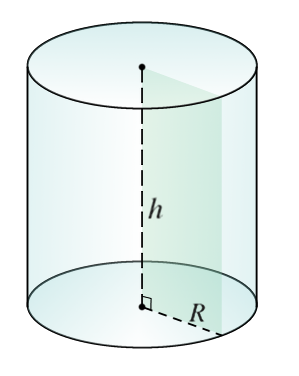
На рисунке 1 изображен прямой круговой цилиндр. Прямой — означает, что угол между осью цилиндра и плоскостью основания — прямой (равен 90 град.), круговой — означает, что в основании цилиндра лежит круг.
Для построения развертки прямого кругового цилиндра потребуются две величины: 1) высота цилиндра (H), 2) диаметр круга, который лежит в основании (D),
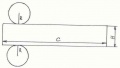
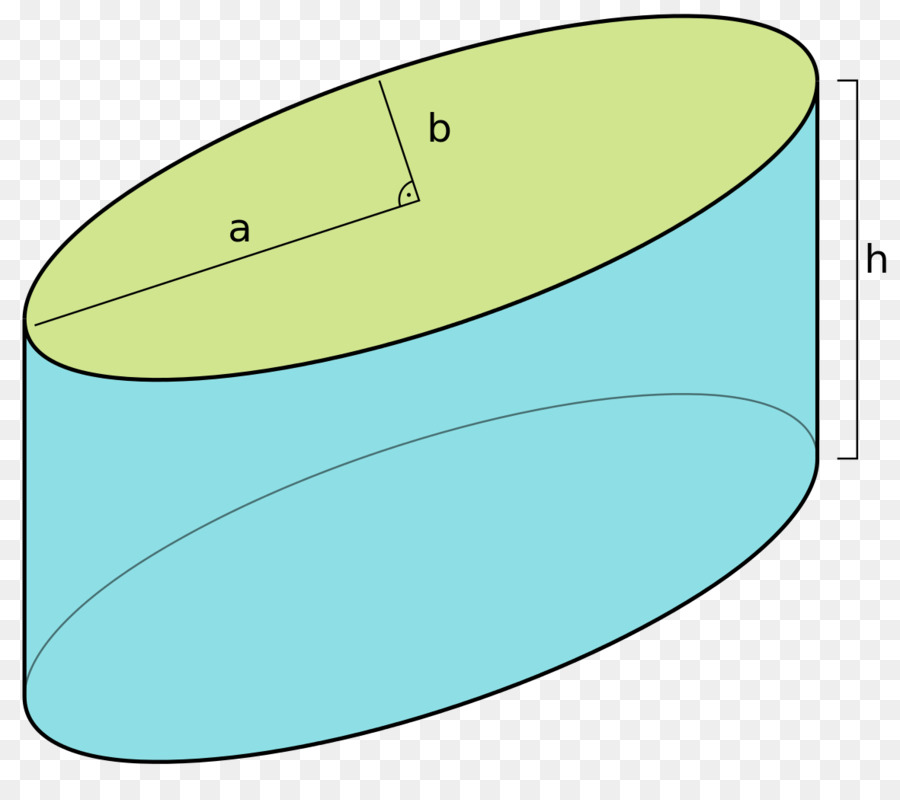
Цилиндр может быть не круговым. Например на рисунке 2 изображен овальный цилиндр. Овальный — означает, что в основании цилиндра лежит овал.
Также, цилиндр может быть не прямым, а наклонным. У наклонного цилиндра (меньше 90 град.). На рисунке 3 изображен наклонный цилиндр.
Для построения развертки наклонного цилиндра потребуются три размера: 1) высота цилиндра (H), 2) радиус окружности (R), 3) угол наклона оси (A), Перейти к построению.
Читайте также: Как снять рабочий цилиндр сцепления ауди 100 с4
Видео:Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать
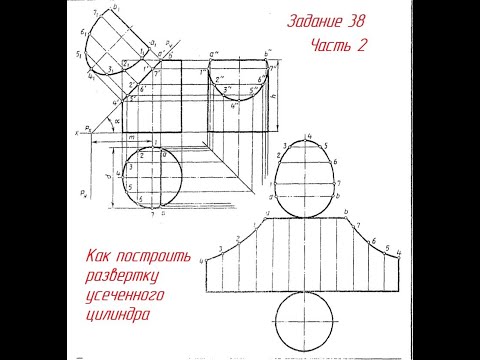
Круглый прямой цилиндр, развертка и формула для ее площади
Цилиндр — это одна из пространственных фигур, которая является объектом изучения стереометрии. Важная характеристика любой фигуры — это площадь ее поверхности. В данной статье рассмотрим, что собой представляет развертка цилиндра, а также покажем, как вычислить ее площадь.
Видео:Уроки Solidworks.Развёртка цилиндраСкачать

Цилиндр как фигура геометрии
Предположим, что у нас имеется некоторая плавная кривая. Это может быть круг, эллипс, парабола и так далее. Возьмем отрезок произвольной длины, который не лежит в плоскости кривой, и опишем с помощью него поверхность, следуя направлению кривой и транслируя отрезок параллельно самому себе. Полученная поверхность называется цилиндрической или просто цилиндром. Отмеченная кривая называется директрисой (направляющей), а отрезок — генератрисой (образующей).
Если к цилиндрической поверхности добавить еще две плоские одинаковые фигуры, ограничивающие эту поверхность с торцов, то полученное тело также называется цилиндром. Оно состоит из двух равных оснований и цилиндрической поверхности.
Для наглядного представления описанной фигуры ниже приведен рисунок. На нем изображен эллиптический цилиндр, имеющий полуоси a и b и высоту h (дистанция между основаниями).
Видео:Как начертить развёртку поверхностей цилиндра #чертёж #развёртка #цилиндрСкачать

Круглый прямой цилиндр
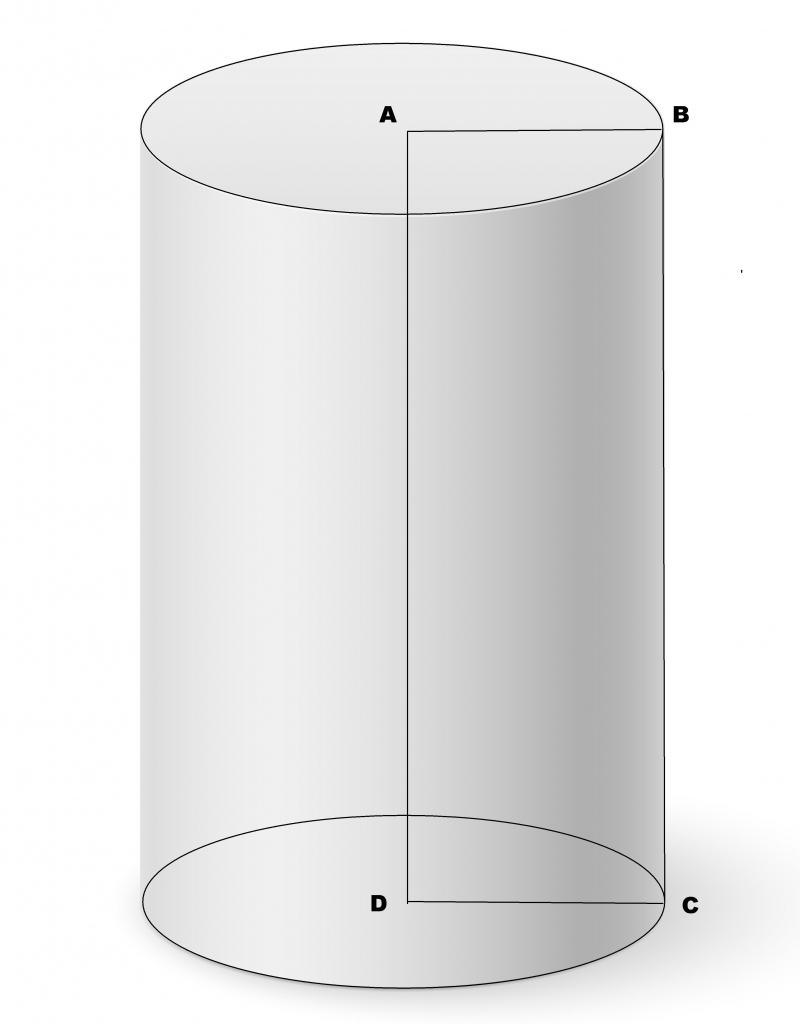
Пусть директрисой будет окружность некоторого радиуса. Тогда образованная генератрисой фигура будет называться круглым цилиндром. Тем не менее генератриса относительно плоскости, ограниченной директрисой, может быть направлена произвольным образом. Поэтому в общем случае говорят о наклонном круглом цилиндре. Если же генератриса будет перпендикулярна плоскостям основания, то цилиндр называется прямым. Он показан на рисунке ниже.
Здесь AB = DC — радиус цилиндра, AD = BC = h — высота фигуры. Для прямого цилиндра высота всегда равна длине образующей. Отрезок AD обозначает ось цилиндра — прямая, соединяющая две центральные точки оснований. От оси цилиндра все точки боковой поверхности лежат на одном расстоянии, равном радиусу фигуры.
Далее в статье будем рассматривать развертку поверхности цилиндра, круглого и прямого.
Видео:Развертка цилиндраСкачать

Развертка круглого прямого цилиндра
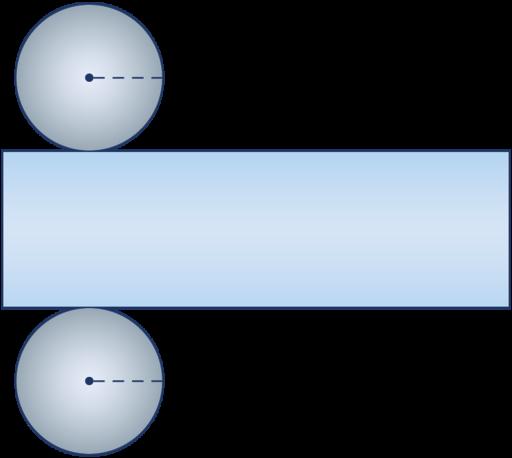
Когда говорят о развертке цилиндра, то подразумевают общую площадь его поверхности, представленную плоскими фигурами. Круглый прямой цилиндр образован двумя кругами, имеющими одинаковые радиусы, и одной боковой поверхностью, которая эти круги соединяет друг с другом.
На рисунке показан бумажный цилиндр. Как осуществляется построение развертки цилиндра? Возьмем воображаемые ножницы и отрежем одно основание вдоль окружности. Затем проделаем аналогичные действия со вторым основанием. Боковую поверхность разрежем вдоль генератрисы, то есть параллельно оси фигуры, и развернем ее. Таким образом, мы получили развертку, которая показана на рисунке ниже.
Очевидно, что она состоит из двух одинаковых кругов. Что касается цилиндрической поверхности, то в разрезанном виде она представлена прямоугольником. Развертку удобно использовать при определении площади поверхности рассматриваемой фигуры.
Видео:Простой расчёт развёртки конусаСкачать

Площадь развертки цилиндра
Выше мы показали, как можно получить развертку фигуры. Чтобы рассчитать ее площадь, необходимо сложить площади для всех ее частей, то есть для двух круглых оснований и одного прямоугольника.
Читайте также: Ремонт задних тормозных цилиндров фольксваген
Обозначим радиус основания буквой r, а высоту фигуры — буквой h. Площадь одного основания равна площади круга, то есть:
Здесь pi — число Пи, приблизительно равное 3,14.
Чтобы вычислить площадь прямоугольника, представляющего боковую поверхность фигуры в развернутом виде, необходимо знать две его стороны. Одна из них равна высоте h. Вторая, как можно догадаться, соответствует длине директрисы, то есть длине окружности. Обозначим ее l. Тогда можно записать следующие равенства:
Здесь Sb — площадь прямоугольника, равная площади цилиндрической поверхности.
Учитывая, что фигура имеет два основания, складываем рассчитанные величины, получаем общую площадь развертки цилиндра:
Площадь S фигуры однозначно определяется через ее радиус и высоту.
Покажем, как использовать это равенство для решения геометрической задачи.
Видео:[Начертательная геометрия] Развертка цилиндра или как сделать развертку цилиндраСкачать
![[Начертательная геометрия] Развертка цилиндра или как сделать развертку цилиндра](https://i.ytimg.com/vi/Gh2jo9L_8gs/0.jpg)
Задача на нахождение радиуса фигуры
Известно, что общая поверхность круглого прямого цилиндра составляет 60 см 2 . Чему равен радиус основания цилиндра, если его высота равна 7 см, а фигура имеет лишь одно основание.
Описанный в условии задачи цилиндр представляет собой бочку без крышки, поэтому площадь его поверхности образована не двумя, а одним основанием.
Если учесть названный факт, тогда формула для площади фигуры запишется в следующем виде:
Подставим все известные из условия величины в это равенство, получим:
Мы получили классическое полное квадратное уравнение. Его решение даст искомое значение радиуса r. Решаем через дискриминант:
При решении уравнения отрицательный корень был отброшен, в виду его нефизического значения.
Таким образом, параметры открытого цилиндра из условия задачи составляют 7 см в высоту и 2,5 см в диаметре.
Видео:Как сделать развертку цилиндра в SolidWorksСкачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Видео:Как сделать развертку цилиндра Scooter.rv.uaСкачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Развертка прямого кругового цилиндра.
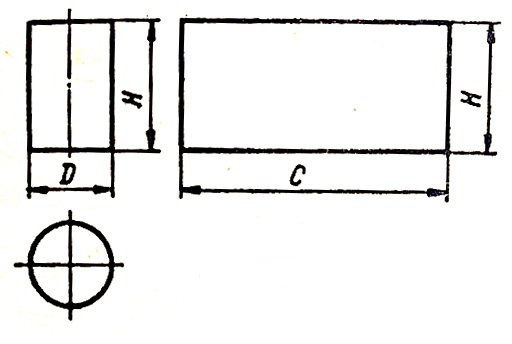
Цилиндр диаметром D и высотой H показан на рис. 1. Развертка представляет собой прямоугольник длиной с = πD и высотой Н.
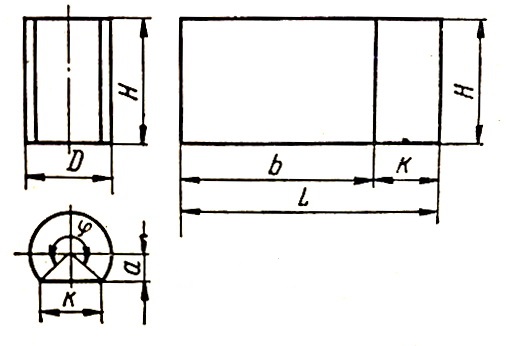
Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2) 2 – a 2 ) = 2a tg (ᵠ/2).
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
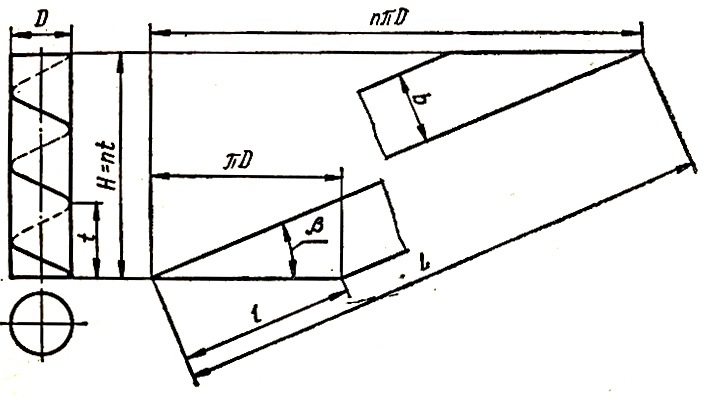
Цилиндр показан на рис. 3. При определении развертки можно использовать следующие зависимости:
n — число полных витков на общей длине цилиндра H, Н = nt;
Развертка усеченного цилиндра.
Для получения развертки горизонтальная проекция цилиндра делится на равные части и точки деления нумеруются (в данном случае от 0 до 12). Из точек деления проводятся вертикали до пересечения верхнего основания в точках 0′1, 1′1…, 6′1. На продолжении прямой 0’6′ откладывается отрезок длиной с = πD, который делится на принятое число равных частей. Из точек деления 00, 10, …, 60 строятся перпендикуляры до их пересечения с соответствующими горизонтальными линиями в точках 0 0 1, 1 0 1, …, 6 0 1. Полученные точки соединяются плавной кривой. Ввиду симметричности остальные точки кривой находит аналогичным путем.
Линию развертки можно определить и таким способом. На расстоянии h1 = (h + H)/2 от линии 0 0 12 0 проводится параллельная прямая. Из центра S, лежащего на прямой, описывается полуокружность радиусом А. Полуокружность делится на равные части, число которых равно половине точек деления развертки (в данном случае на шесть). Через точки деления 0ꞋꞋ, 1ꞋꞋ, …, 6ꞋꞋ проводятся горизонтальные прямые до пересечения вертикалей, проходящих через 0 0 , 1 0 , … , 12 0 . Полученные точки 0 0 1, 1 0 1, …, 12 0 1 соединяются плавной кривой.
Читайте также: Диаметры тормозных цилиндров тойота
Верхнее основание цилиндра представляет собой эллипс с полуосями a = D/2 cos α = 0′13′1 и b = D/2.
При аналитическом определении координат точек кривой развертки цилиндра, усеченного плоскостью под углом α (рис. 5), могут быть использованы следующие зависимости:
xk = kx1 = πD/2 kε/180°; yk = D/2 tg α sin kε = A sin kε = A sin ᵠi,
где х1 = πD/ (2n) = πD/2 ε/180° — длина дуги окружности основания цилиндра, разделенная на 2n равных частей; ε = 360°/2n — центральный угол, соответствующий одному делению; k — порядковый номер точки; A = (H — h)/2 = (D/2) tg α — амплитуда синусоиды; ᵠi= kε.
Значения sin kε для наиболее часто употребляемых значений 2n приведены в табл. 1.
Таблица 1. Значения sin kε и sin 2 kε
| 2n | sin kε | sin 2 kε | 2n | sin kε | sin 2 kε | ||||||
| 8 | 16 | 32 | 64 | 12 | 24 | 48 | 96 | ||||
| — | — | — | 1 | 0,09802 | 0,00961 | — | — | — | 1 | 0,06540 | 0,00428 |
| — | — | 1 | 2 | 0,19509 | 0,03806 | — | — | 1 | 2 | 0,13053 | 0,01704 |
| — | — | — | 3 | 0,29028 | 0,08426 | — | — | — | 3 | 0,19509 | 0,03806 |
| — | 1 | 2 | 4 | 0,38268 | 0,14645 | — | 1 | 2 | 4 | 0,25882 | 0,06699 |
| — | — | — | 5 | 0,47139 | 0,22221 | — | — | — | 5 | 0,32144 | 0,10332 |
| — | — | 3 | 6 | 0,55557 | 0,30866 | — | — | 3 | 6 | 0,38268 | 0,14645 |
| — | — | — | 7 | 0,63439 | 0,40245 | — | — | — | 7 | 0,44229 | 0,19562 |
| 1 | 2 | 4 | 8 | 0,70711 | 0,50000 | 1 | 2 | 4 | 8 | 0,50000 | 0,25000 |
| — | — | — | 9 | 0,77301 | 0,59754 | — | — | — | 9 | 0,55557 | 0,30866 |
| — | — | 5 | 10 | 0,83147 | 0,69134 | — | — | 5 | 10 | 0,60876 | 0,37059 |
| — | — | — | 11 | 0,88192 | 0,77778 | — | — | — | 11 | 0,65935 | 0,43474 |
| — | 3 | 6 | 12 | 0,92388 | 0,85355 | — | 3 | 6 | 12 | 0,70711 | 0,50000 |
| — | — | — | 13 | 0,95694 | 0,91573 | — | — | — | 13 | 0,75184 | 0,56526 |
| — | — | 7 | 14 | 0,98079 | 0,96194 | — | — | 7 | 14 | 0,79335 | 0,62941 |
| — | — | — | 15 | 0,99518 | 0,99039 | — | — | — | 15 | 0,83147 | 0,69134 |
| 2 | 4 | 8 | 16 | 1,00000 | 1,00000 | 2 | 4 | 8 | 16 | 0,86617 | 0,75000 |
| — | — | — | 17 | 0,89687 | 0,80438 | ||||||
| — | — | 9 | 18 | 0,92388 | 0,85355 | ||||||
| — | — | — | 19 | 0,94693 | 0,89668 | ||||||
| — | 5 | 10 | 20 | 0,96600 | 0,93301 | ||||||
| — | — | — | 21 | 0,98079 | 0,96194 | ||||||
| — | — | 11 | 22 | 0,99144 | 0,98296 | ||||||
| — | — | — | 23 | 0,99786 | 0,99572 | ||||||
| 3 | 6 | 12 | 24 | 1,00000 | 1,00000 | ||||||
Примечание: Значения sin kε и sin 2 kε даны для одной четверти окружности. В остальных четвертях они повторяются.
Ввиду симметричности синусоиды достаточно определить координаты точек одной четверти окружности, например от у0 до у3. Остальные координаты имеют соответственно равные значения. Например: у4 — у2, …, у11 = — у1 и т. д.
💥 Видео
[Начертательная геометрия] Как сделать развертку цилиндра (построение в AutoCAD)Скачать
![[Начертательная геометрия] Как сделать развертку цилиндра (построение в AutoCAD)](https://i.ytimg.com/vi/XqmGLELwdX0/0.jpg)
Как сделать ИДЕАЛЬНЫЙ цилиндр из бумагиСкачать

Уроки Компас 3D.Развертка цилиндраСкачать

усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Развертка цилиндра в SolidWorks. Техподдержка Курс №1Скачать

Построение разверток в Autodesk InventorСкачать

Развёртка цилиндраСкачать

Построение развертки конусаСкачать
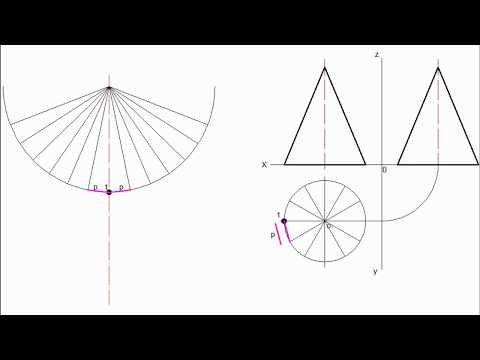
[Начертательная геометрия] Как построить развертку конусаСкачать
![[Начертательная геометрия] Как построить развертку конуса](https://i.ytimg.com/vi/ZIPjD9hsAUo/0.jpg)
КАК СДЕЛАТЬ ЦИЛИНДР ИЗ БУМАГИ? КАК СДЕЛАТЬ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ? ГЕОМЕТРИЧЕСКИЕ ТЕЛА. | #RAIDOTVСкачать