Как располагается цилиндр в проекции гаусса крюгера (3 видео)

Содержание

Метод формирования изображения в проекции Гаусса-Крюгера
Введение
Метод «GKZone»
Заключение
Список литературы
От автора
Равноугольная поперечно-цилиндрическая проекция Гаусса-Крюгера
Как располагается цилиндр в проекции гаусса крюгера
🔥 Видео

Видео:Системы координат в геодезии. Зональная система прямоугольных координат. Гаусса-КрюгераСкачать

Метод формирования изображения в проекции Гаусса-Крюгера

Введение

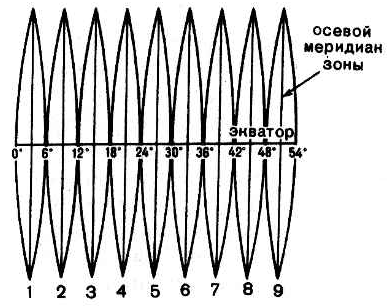
При формировании картографического изображения местности в поперечной равноугольной цилиндрической проекции Гаусса-Крюгера возникают проблемы, связанные с большими погрешностями и искажением формируемого изображения при удалении от осевого меридиана. Корнем этих проблем является то, что проекция Гаусса-Крюгера представляет собой шестьдесят “лепестков” шести-градусных зон, между которыми искусственно вносится расстояние 500 км. Это происходит из-за того, что стандартные методы визуализации не учитывают сужение зон к полюсам, а представляют их как прямоугольные. Для преодоления этих проблем существуют методы сшивания карт по одному осевому меридиану.

Метод «GKZone»

Одним из таких методов является метод динамического совмещения осевых меридианов, позволяющий компенсировать угол и расстояние между ними. Использование такого метода позволяет отобразить 2D карту в проекции Гаусса-Крюгера без видимых искажений, а также избежать избыточности исходных данных. Принцип данного метода состоит в том, что множество фрагментов листа карты, полученных при подготовке массивов данных, формируют, так называемые, зоны-лепестки.
Для увеличения точности расположения объектов и уменьшения визуального искажение (ничтожно малое), можно задать нестандартный размер одной зоны равной, например, 1º или даже меньше. Размеры фрагментов, которыми заполняются зоны, задаются произвольно. Чем меньше размер фрагмент, тем выше качество визуализации.

Рисунок 1. Пример разделения развернутой земной поверхности на зоны с шагом 6º

Метод совмещения заключается в следующем:

Совершить пересчет координат точки интереса(относительно широты которой производиться склеивания) из геодезической/геоцентрической системы координат в проекцию Гауса-Крюгера.
Определить координаты двух точек соприкосновения соседних осевых меридианов.
Рассчитать угол поворота одной зоны относительно другой на текущей широте.
Исходя из полученного угла сформировать матрицу преобразования для каждых соседних меридианов.
Для позиционирования фрагмента необходимо умножить его координаты на соответствующую матрицу преобразования.

После выполнения перечисленных действий, мы получаем неразрывную сшитую карту. На рисунках 2 и 3 представлены изображения сшитых зон относительно различных северных широт.

Рисунок 2. Сшито на 20° с.ш.

Рисунок 3. Сшито на 50° с.ш.

Причем координата широты у фрагментов склеиваемых зон остается неизменной, изменяется только координаты долготы. При слиянии зон таким способом, во время визуализации картографической информации местности, полностью отсутствует зрительная деформация и минимизируется погрешность. На рисунке 4 показано, что окружность будет изображена без видимых искажений, если карта будет сшита описываемым образом.

Рисунок 4. Изображение окружности

Заключение

Большое значение в визуализации картографической информации имеет качество изображения, но минимизация погрешностей отображения и возможность расчета приблизительного расстояния по полученному изображению также играет большую роль. Описанный метод удовлетворяет оба параметра и успешно используется при разработке картографических систем.

К сожалению данный метод применим только для карт масштабов до 1:1000000, так как при увеличении масштаба становятся явно видны участки совмещения.

Список литературы

Курс высшей геодезии, П, С. Закатов, Москва «НЕДРА» 1976
ГОСТ Р51794-2008

От автора

Данная статья является выдержкой из статьи для будущей конференции. Детали и расчеты я решил пока не выкладывать, так как они еще редактируются. Название метода — GKZone, конечно не самое удачное, но это рабочее название метода в исходном коде. Поэтому приветствуются предложения по более понятному названию метода.

Надеюсь данная статья будет полезна для людей, интересующихся картографией, потому что проекция Меркатора широко освещена в различных источниках, а проекция Гаусса-Крюгера нет.

Жду конструктивной критики статьи и предложений по ее улучшению.

Читайте также: Для чего предназначен главный цилиндр сцепления

Видео:Системы координат, применяемые в геодезииСкачать

Равноугольная поперечно-цилиндрическая проекция Гаусса-Крюгера

Для всех топографических карт в нашей стране применяется проекция Гаусса-Крюгера. Проекция равноугольная, средний меридиан изображается прямой линией без искажений, экватор изображается прямой, перпендикулярной к среднему меридиану. Все остальные меридианы криволинейны и симметричны относительно среднего меридиана и экватора.

Полоса отображения в проекции представляет собой шестиградусную или трехградусную зону эллипсоида.

Координатными осями для каждой зоны являются прямолинейный средний меридиан – ось абсцисс и прямолинейный экватор – ось ординат. Счет координатных зон при разбиении земного эллипсоида ведется с запада на восток. Долгота осевого меридиана первой зоны равна 3° (т.к. он посередине зоны, а отсчет этой зоны идет от Гринвичского меридиана). Номер зоны N и долгота осевого меридиана L° связаны равенством

L° = 6°N – 3°

Номер зоны N в проекции Гаусса-Крюгера отличается от номера колонны карты масштаба 1:1 000 000 на 30.

Например, если номенклатура листа карты N-45, то это значит, что лист расположен в 15 зоне проекции Гаусса-Крюгера и его осевой меридиан имеет долготу

L° =6°х15-3° = 90°-3° = 87°

Для построения топографических карт России прибегают к многополосному изображению земного эллипсоида, когда на плоскость переносят зоны эллипсоида, протяженностью 6° (рис.2.20).

Каждая зона строится на отдельном касательном поперечном цилиндре так, что ось касания проходит по среднему меридиану зоны PP΄, называемому осевым (рис.2.21). У каждой зоны свой осевой меридиан.

Рис. 2.20. Схема многополосного изображения земного эллипсоида

При развертывании цилиндра в плоскость осевой меридиан изображается без искажения прямой PP΄ (рис.2.22) и его принимают за ось xx. Экватор EE΄ также изображается прямой, перпендикулярной к осевому меридиану. Он соответствует оси yy. Началом координат в каждой зоне служит точка О – пересечение осевого меридиана и экватора. Таким образом, положение любой точки определяется прямоугольными координатами x и y.

Рис. 2.21. Схема развертывания поверхности эллипсоида
с помощью цилиндра

Рис. 2.22. Результат развертывания цилиндра на плоскости

Разграфка и номенклатура листов топографических карт и планов

Классификация карт и планов по масштабу осуществляется следующим образом:

1. Планы

1 : 500

1 : 1 000

1 : 2 000

1 : 5 000

2. Крупномасштабные (детальные) топографические карты

1 : 10 000

1 : 25 000

1 : 50 000

1 : 100 000

3. Среднемасштабные (обзорно-топографические) карты

1 : 200 000

1 : 300 000

1 : 500 000

1 : 1 000 000

4. Мелкомасштабные (обзорные) карты

1 : 2 500 000

1 : 4 000 000

1 : 8 000 000

1 : 20 000 000

Лист топографической карты любого масштаба по размерам должен быть удобным как при его создании, печатании тиража, так и при пользовании им. С учетом этого установлено, что размер одного листа не должен быть больше 50см х 50 см. Но на одном таком листе изображается незначительный участок местности, поэтому карты на значительную (обширную) территорию являются многолистными.

Определение 2.9. Система разделения карты или плана на отдельные листы называется разграфкой карты (плана).

Определение 2.10. Обозначение отдельных листов многолистных топографических карт и планов в единой системе есть номенклатура.

Система разграфки и номенклатура листов карт и планов отдельных масштабов дают возможность определять географические координаты углов рамки любого листа топографической карты всего масштабного ряда, а также по географическим координатам точки находить номенклатуру листа карты любого масштаба, на котором эта точка находится, а также находить прямоугольные координаты. Лист карты масштаба 1 : 1 000 000 получается разбиением параллелями через 4°, а меридианами – через 6°.

Географические координаты углов рамки листа карты масштаба 1 : 1 000 000 по его номенклатуре определяют следующим образом.

Читайте также: Защелка под цилиндр palidore 2045 рс хром пластик

Порядковый номер в виде буквы латинского алфавита, которая принимает конкретное значение – числа натурального ряда и которой обозначен ряд, умножают на 4° и получают географическую (геодезическую) широту северной параллели. Для колонн с номерами 31-60 (к востоку от Гринвича) номер колонн уменьшают на 30. Тогда формула для расчета географической (геодезической) долготы восточного меридиана (правого угла листа) будет выглядеть

Соответствие масштабов и номенклатуры листов приведено в табл.1.

Таблица 1. Масштабы и номенклатура листов карты

Масштаб	Номенклатура	Размер листа
по широте	по долготе
1:1000000	N-37	4°	6°
1:500000	N-37-А (от А до Г)	2°	3°
1:200000	N-37-XXXVI (от I до XXXVI)	0°40¢	1°
1:100000	N-37-144 (от 1 до 144)	0°20¢	0°30¢
1:50000	N-37-144-Г (от А до Г)	10¢	15¢
1:25000	N-37-144-Г-г (от а до г)	5¢	7¢30²
1:10000	N-37-144-Г-г-4 (от 1 до 4)	2¢30²	3¢45²
1:5000	N-37-144-256	1¢15²	1¢52²5
1:2000	N-37-144-256-u	0¢25²	0¢37²5

Последние две строки для планов местности с площадью S > 20 км 2 .

Пример. Пусть N = 14 – порядковый номер ряда, тогда

СШ = 14 х 4° = 56°; ЮШ = 56° – 4° = 52° (учли, что отсчет угла идет от плоскости экватора)

Переход от листа карты масштаба 1 : 1 000 000 к листам карт других масштабов осуществляется по простейшему алгоритму, приведенному на рис. 2.23.

Рис. 2.23. Схема алгоритма разграфки

Вопросы и задания для самопроверки

1. Почему для российских картографов важна модель Земли в виде эллипсоида Красовского?

2. Проведите анализ, в какой системе координат – географической или геодезической – можно получить более точные координаты реальных объектов.

3. Какой линейный масштаб чаще всего подписывается на картах?

4. Проанализируйте, каким образом на функциях , , и может сказаться требование, чтобы изображение картируемого объекта при переходе с поверхности эллипсоида на плоскость карты было однозначным и непрерывным.

5. Покажите, что все виды искажений в картографических проекциях связаны друг с другом.

6. Почему, на ваш взгляд, используется такое большое число (несколько десятков) картографических проекций?

7. Приведите примеры производных проекций, получаемых преобразованием известных вам проекций.

8. Пользуясь номенклатурой листов из табл. 1, продолжите схему алгоритма разграфки, изображенную на рис. 2.23, для карт других масштабов.

9. Почему работа с электронными картами более удобная и производительная, чем с картами на твердом носителе?

Дата добавления: 2015-07-06 ; просмотров: 4144 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:42 Картографические проекцииСкачать

Как располагается цилиндр в проекции гаусса крюгера

Проекция Гаусса-Крюгера — это поперечная цилиндрическая равноугольная картографическая проекция, разработанная немецкими учёными Гауссом и Крюгером. Применение этой проекции даёт возможность практически без существенных искажений изобразить довольно значительные участки земной поверхности и, что очень важно, построить на этой территории систему плоских прямоугольных координат.

В 1928 г. на III геодезическом совещании для всех геодезических и топографических работ в СССР была принята проекция Гаусса-Крюгера на эллипсоиде Бесселя. В этой проекции начали создавать топографические карты масштабов крупнее 1:500 000, а с 1939 г. проекция Гаусса-Крюгера стала применяться и для карты масштаба 1:500 000. В апреле 1946 г. постановлением правительства были утверждены размеры референц эллипсоида Крассовского и новые исходные даты, характеризующие систему координат 1942 г.

В проекции Гаусса-Крюгера поверхность эллипсоида на плоскости отображается по меридианным зонам, ширина которых равна 6° (для карт масштабов 1:500 000-1:10 000) и 3° (для карт масштабов 1:5 000- 1:2 000). Меридианы и параллели изображаются кривыми, симметричными относительно осевого меридиана зоны и экватора, однако их кривизна настолько мала, что западная и восточная рамки карты изображаются прямыми линиями. Параллели, совпадающие с северной и южной рамками карт, изображаются прямыми на картах крупных масштабов (1:2 000-1:50 000), на картах мелких масштабов они изображаются кривыми. Начало прямоугольных координат каждой зоны находится в точке пересечения осевого меридиана зоны с экватором. В России стране принята нумерация зон, отличающаяся от нумерации колонн карты масштаба 1:1 000000 на тридцать единиц, то есть крайняя западная-зона с долготой осевого меридиана L=21 имеет номер 4, к востоку номера зон возрастают. Номер зоны N и долгота осевого меридиана L° в градусах связаны между собой равенством L° == 6N- 3.

Читайте также: Как очистить блок цилиндров от нагара

Территория России находится в северном полушарии, поэтому координаты ^ Х всех точек имеют положительное значение. Координаты Y имеют отрицательные значения левее осевого меридиана и положительные правее его. Чтобы исключить из обращения отрицательные координаты и облегчить пользование прямоугольными координатами на топографических картах, ко всем координатам Y добавляют постоянное число 500 000 м. Для указания зоны, к которой относятся координаты, к значению Y слева приписывают номер зоны. Например, запись координаты Y» 30 786 543 м означает, что точка находится в 30-й зоне, ее реальная координата равна 786 000- 500 000 = 286 543 м, то есть она расположена правее осевого меридиана 30-й зоны. Запись координаты Y= 8 397 720 м означает, что точка находится в 8-й зоне, ее реальная координата равна 397 720- 500 000 = 102 280 м, она расположена левее осевого меридиана 8-й зоны.

Рисунок 30. Проекция Гаусса-Крюгера

При создании любых карт важное значение имеет вопрос о выборе картографической проекции, которая обеспечит возможность оптимального решения по этим картам различных задач. Какая проекция будет использована при работе в первую очередь зависит от назначения карты и её масштаба, которыми часто обусловливается характер допускаемых искажений в избираемой проекции. Так же существуют методики по выбору проекций.

Карты крупных и средних масштабов, предназначенные для решения метрических задач, обычно составляют в равноугольных проекциях, а карты мелких масштабов, используемые для общих обозрений и определения соотношения площадей каких-либо территорий- в равновеликих. При выборе проекций начинают с простейших, затем переходят к более сложным проекциям, даже, возможно, модифицируя их.

Для изображения России удобны конические проекции, в которых воображаемый конус рассекает земной шар по параллелям 47 и 62° северной широты: на создаваемых подобным образом картах это так называемые линии нулевых искажений. Вблизи них сжатия и растяжения невелики, что удобно, поскольку между ними находятся самые густонаселённые области. Карты Северного Ледовитого океана или Антарктиды чаще всего составляются в азимутальной проекции, расположив воображаемую вспомогательную плоскость так, чтобы она касалась полюса. Тогда растяжения в полярных областях земли окажутся минимальными. В современной картографии достаточно большой набор проекций для любых карт (планета в целом, материки и океаны, страны и т. д.) и всевозможного назначения.

Для того, чтобы перейти из одной системы координат в другую используется набор параметров, которые определяют отличие эллипсоида на котором базируется одна СК от другого. Это так называемые линейные элементы трансформирования определяющие сдвиг центра масс эллипсоида относительно общеземного и угловые элементы трансформирования определяющие соответственно поворот эллипсоида относительно общеземного. Если видно, что какие то данные равномерно смещены относительно других слоев на одинаковую величину, то скорее всего используются данные находящиеся в разных системах координат.