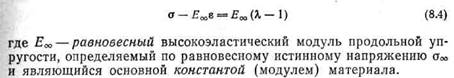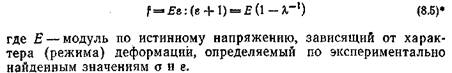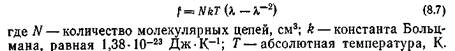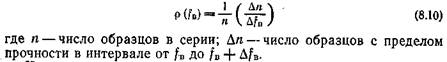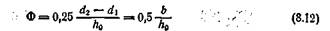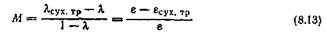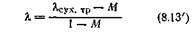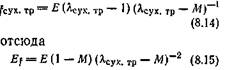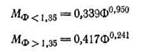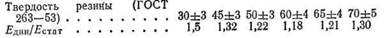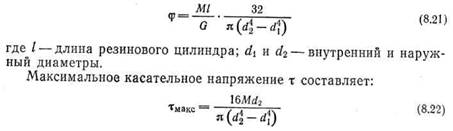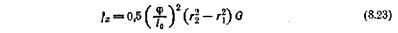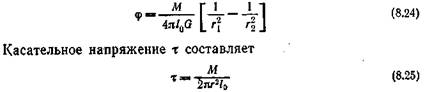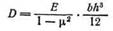Как рассчитать деформацию шины

Деформация – это изменение размеров или формы твердого тела под действием внешних сил. Применимо к шинам можно выделить два типа деформаций:

• Функциональная деформация;
• Критическая деформация.

Деформация функциональная входит в круг обязанностей, которые должна выполнять современная шина. А именно – деформироваться, снижая вибрационное и шумовое воздействие на автомобиль и водителя, которое возникает при качении шины по поверхности дороги. Гибкость структуры шины, а также правильное давление внутри позволяют шине без проблем выполнять данную функцию, совершая при этом огромное количество деформаций на единицу времени без негативных последствий.

Критическая деформация как раз и характеризуется тем, что следствием ее может являться полное или частичное разрушение шины, исключающее ее дальнейшее использование. К критическим деформациям можно отнести:

— возникающую при длительном стоянии автомобиля;

— являющуюся следствием езды с давлением ниже рекомендованного;

— шоковую с разрушением боковины.

Деформация шины, возникающая при неправильном хранении

Повреждения, которые получает шина при нарушении правил хранения шин, являются довольно распространенными эксплуатационными повреждениями, которые не являются следствием выполнения шиной своих функций. Среди данного типа критических деформаций встречаются следующие повреждения шины:

— излом бортового кольца, возникающий при длительном хранении шин «елочкой». К сожалению, хранение подобным способом являются очень распространенной практикой, хотя шинные производители рекомендуют использовать его только ограниченное время, необходимое для перевозки шин. Излом бортового кольца является неремонтопригодным дефектом, и устанавливать такие шины на диски не рекомендуется.

Как избежать:

Необходимо внимательно осматривать новые шины при получении: бортовые кольца шины должны иметь строгую круглую форму без минимального излома. Кроме этого, при длительном хранении рекомендуется ставить шины на протектор, в вертикальном положении, используя специальные стеллажи, не повреждающие шины.

— искривление шины при хранении в стопках. Подобный способ хранения по-прежнему часто встречается, и он также особо опасен для тех шин, что оказались внизу стопки. И чем выше данная конструкция, тем сильнее страдает нижние шины. Подобное хранение может привести к внутреннему искривлению шины, что, в свою очередь, может стать причиной увода шины в сторону, а также к нерегулируемому дисбалансу или вибрации.

Как избежать:

Покупать шины в профессиональных шинных центрах и избегать тех магазинов, где в торговом зале находится огромное количество стопок шин (более четырех шин высотой). Так как внутреннее искривление шины нельзя увидеть при визуальном осмотре, и только балансировочный станок поможет выявить первые признаки проблем с шиной. При хранении шин собственником необходимо также избегать хранения стопкой, пусть даже количество шин ограничено четырьмя.

Деформация шины, возникающая при длительном стоянии автомобиля

Мало кто знает о том, что шины могут повредиться и от долгого пребывания в вертикальном положении, с воздухом внутри. Как правило, это возможно при стоянке автомобиля на одном месте. Подобное положение деформирует шину, лишая ее идеально круглой формы. При езде на такой шине могут появиться вибрации, шум. Возможно и неремонтопригодное повреждение внутренней структуры шины, особенно у шин, бывших до этого долгое время в эксплуатации.

Как избежать:

В технических документах рекомендуется ограничить срок подобного длительного пребывания до двух суток для автомобилей с полной загрузкой и до десяти суток для ненагруженных транспортных средств. При необходимости более продолжительной стоянки автомобилей следует снижать нагрузку на шины с помощью подставок или передвижения автомобиля.

Деформация шины вследствие езды на низком давлении

Одной из самых распространенных форм критической деформации является необратимое изменение шины, которое происходит из-за эксплуатации шины с низким внутренним давлением. Из-за этой недостаточности обычные рабочие деформации становятся излишними, и стенки шины, не рассчитанные на чрезмерное изгибание, начинают нагреваться сверх меры. Таким образом начинается разрушение самой шины. Вначале разрушается герметизирующий слой: он начинает бугриться на внутренней поверхности стыка боковины и беговой дорожки, затем идет его отслоение, образуется резиновый намол. Затем боковина, оголенная до нитей каркаса, начинает трескаться, и воздух покидает шину. Дальнейшая езда на такой шине может привести к полному отделению боковины от протектора.

Как избежать:

Следить за давлением. Кроме проверки, нужно регулярно менять вентили, своевременно и качественно ремонтировать шины, не допускать езды на шинах с повреждениями. Так как все это может привести к медленной потере давления и к появлению критической деформации шины.

Видео:Как считать размер шин. Расчёт и расшифровка размеров и обозначений.Скачать

Деформация шины при шоковой ударной нагрузке

При попадании шины в яму, наезде на посторонний предмет на дороге может возникнуть деформация шины, которая может единовременно уничтожить изделие. Если это происходит на высокой скорости, а края ямы или предмета достаточно твердые и острые, то шансы на мгновенное разрушение шины существенно возрастают. В такой ситуации происходит защемление боковины шины между диском и поверхностью, например, в ямах. Воздействие прочих факторов (скорость, агрессивность препятствия) приводит к появлению ударной силы, которая разрывает несколько нитей каркаса. Ослабленное место боковины шины легко деформируется внутренним давлением, и появляется грыжа. Дальнейшая эксплуатация шины не рекомендуется. Стоит отметить, что иногда разрыв нитей каркаса сопровождается разрывом внутренних и внешних слоев боковины шины, приводящим к потере давления, что, конечно же, исключает дальнейший ремонт шины и ее использование.

Как избежать:

Осторожно, снижая скорость, проезжать участки дороги с плохим покрытием, не допускать наездов на бордюрные камни и прочие посторонние предметы. Если плохие дороги – достаточно частое явление, то не лишним будет обратить внимание на технологии, защищающие шины от повреждения. Например, компания Мишлен использует технологию IronFlex для некоторых своих моделей (MICHELIN Energy XM2, X-Ice North 3, X-Ice 3), которая снижает вероятность повреждения боковины шины при шоковой деформации. С этой же целью применяется двойной каркас для внедорожных шин семейства Latitude, что также снижает вероятность преждевременного выхода шины из эксплуатации по причине повреждения нитей каркаса.

Аналитическая зависимость между напряжением и деформацией резины и ее механические свойства

Растяжение в одноосном нагружении. При одноосном растя­жении с постоянной скоростью кристаллических материалов до ве­личины деформации, отвечающей пределу упругости (пропорциональности), наблюдается линейная зависимость между условным напряжением f (в 10 Н/см 2 ) и соответствующей ему относительной деформацией е. Для различных материалов их пределы пропорциональности различны как абсолютно, так и относительно к их пре­дельной деформации при разрыве.

Материалы, обладающие (наряду с упругой) высокоэластиче­ской деформацией — каучук, резина, некоторые пластмассы, а также текстильные изделия, способные при одноосном нагружении к значительно большим растяжениям, чем, например, сталь и раз личные металлы — линейную зависимость f — e показывают лишь на весьма небольших начальных растяжениях. В целом у этих материалов, несмотря на большую обратимость деформации, за­висимость f — е нелинейна и обычно не монотонна. Следовательно, такие материалы, как не отвечающие известному положению Гука, нельзя охарактеризовать одним постоянным значением модуля продольной упругости Ef, рассчитываемого по условному напряже­нию f. На участке нелинейной зависимости модуль материала Ef можно определять лишь в дифференциальной форме.

Применяемый иногда местный модуль (модуль по хорде) как отношение f/ef не дает конструкционно значащей оценки мате­риала. Столь же несостоятельна применяемая в лабораторной практике оценка свойств резины условным напряжением, отвечаю­щим растяжению на 100, 300 или 500% против начальной длины образца. Эти так называемые «модули» представляют собой лишь ординаты некоторых промежуточных точек кривой f — е, но не константы материала.

Для расчетно-конструкторских целей желательно, чтобы анали­тическая зависимость напряжений и соответствующих им дефор­маций резины была выражена через одну, имеющую физический смысл, характеристику материала, не зависящую от деформации. Практически удобно определять деформацию не относительным удлинением е, а величиной л, отношением текущей и начальной длин образца (относительной длиной образца):

Установление, с большим или меньшим приближением, зависи­мости между f (или о) и X для материалов, обладающих высоко эластическими свойствами, возможно: или теоретически, путем вы­числения искомой зависимости из свойств той или иной механиче­ской модели высокомолекулярного соединения, или путем подыскания уравнения экспериментально найденной зависимости.

Теоретическое установление зависимости напряжение — дефор­мация резины для высокоэластического ее состояния исходит из положения, что равновесное деформированное состояние опреде­ляется высокоэластической составляющей и что величиной упругой энергетической составляющей деформации можно пренебречь.

Читайте также: Рейтинг шин hankook winter i cept

Рассматривая равновесную высокоэластическую деформацию резины как явление ориентации цепей молекулярных звеньев кау­чука в силовом поле, Г. М. Бартенев предложил для одноосной деформации растяжения резины следующее уравнение

Уравнение (8.4) применимо для мягких резин с содержанием связанной серы до 8%, но без учета влияния химических про­цессов в период нахождения образца под нагрузкой; последнее при­водит к условно равновесному модулю. Показано также, что уравнение пропорциональности а и е в ограниченных, но практи­чески достаточных пределах деформации с достаточным при­ближением может быть принято не только для равновесной де­формации, но и для статической, а равно и для непериодической динамической, но с другим в каждом конкретном случае модулем материала, зависящим от режима деформации и температуры. Под статической деформацией здесь понимается деформация в равновременном режиме, когда независимо от величины принятой де­формации одинаково время действия силы; под непериодической — динамический равноскоростной режим.

С учетом сказанного, для условного напряжения f при растя­жении справедлива будет приближенная зависимость

По числовому значению модуль Е занимает некоторое проме­жуточное место между мгновенным модулем Е₀, определяющим уп­ругие свойства резины в начальный период деформации, и высоко­эластическим равновесным модулем Еоо. Следуя уравнению (8.5), найдем дифференциальный модуль как производную от напряже­ния по деформации:

В физическом смысле Е по уравнению (8.6) при % Ш 1 представ­ляет модуль начальной деформации в соответственном режиме (то же относится и к E_f при этом значении X).

Уолл предложил следующее уравнение зависимости f — К для ненаполненной резины из натурального каучука

Если это уравнение привести к эмпирическому виду, позво­ляющему проверить его в статиче­ской или непериодической динами­ческой деформации, то получим

По физическому смыслу G в уравнении (8.9) при представ­ляет собой модуль сдвига, равный 1/3 Е для начальной деформации, как это и следует из зависимости G = £ : 2Х (1+M). Для изотроп­ных материалов при малых дефор­мациях и коэффициенте Пуассона м = 0,5.

Видео:Как проверить качество шин при покупке? Проверка качества резины.Скачать

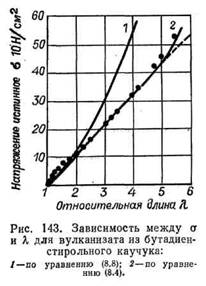
При растяжении ненаполненного вулканизата из бутадиен-сти-рольного каучука до л = 4 — 5 линейное уравнение (8.4) лучше согласуется с экспериментом (рис. 143), чем уравнение (8.8). Для наполненных вулканизатов уравнение (8.4) применимо при­мерно до л = 1,5.

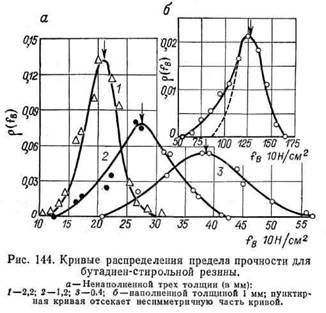
Предел прочности резины при разрыве (как ус­ловный f_B, так и истинный о_в) зависит от ряда факторов. Поэтому в лабораторных испытаниях резины, следуя ГОСТ 270—64, приме­няют образцы установленной формы и размеров в виде двухсто­ронней лопатки, и испытание ведут со скоростью перемещения ниж­него зажима 500 мм/мин. Для инженерных расчетов необходимо было бы уяснение зависимости между пределом прочности резины в стандартных условиях испытания и в изделиях в условиях эксплуатации. Некоторое представление об ожидании такой зависимости следует из данных Г. М. Бартенева, полученных при испытании на разрыв образцов резины в форме стандартных двух­сторонних лопаток различной толщины: 2,2; 1,2 и 0,4 мм. В каж­дой из таких серий испытывалось не менее 100 образцов. Резуль­таты испытаний приведены на рис. 144, где по оси абсцисс откладывался найденный предел прочности, а по оси ординат функция распределения предела прочности р(f_в), рассчитываемая по формуле

Как видно из рис. 144, с уменьшением толщины кривые сме­щаются в сторону больших величин предела прочности, но разброс данных при этом увеличивается. Кривые для ненаполненной ре­зины отвечают нормальному распределению, и наивероятнейшая прочность может быть рассчитана как средняя арифметическая при заданной толщине образцов. В то же время относительный разброс прочности практически не зависит от толщины образцов.

При очень медленном растяжении, отвечающем установлению состояния, близкого к равновесному, предел прочности резины за­висит от степени поперечного «сшивания» и от прочности химиче­ских связей. При конечной же скорости растяжения решающее значение имеют связи межмолекулярного взаимодействия. При прочих равных условиях чем полярнее каучук, тем прочнее мягкий вулканизат. Чем выше скорость растя­жения, тем выше предел прочности (табл. 6).

В конструкции и эксплуатации РТИ могут быть различны не только скорость деформации и толщины образцов, но также другие геометрические размеры, форма образцов, виды и режимы дефор­мации и возможность концентрации на­пряжений. Все это в той или иной мере влияет на величину предела прочности в изделии и на срок службы изделия.

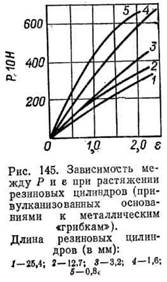
На рис. 145 показана зависимость между нагрузкой Р и относительным удлинением е при растяжении цилиндри­ческих образцов резины одного диаметра, но различной толщины (длины),привулканизованных к металлическим шай­бам (так называемым «грибкам»). Из рис. 145 видно, что чем тоньше образец, тем меньше его относительное удлинение при заданном Р; чем толще образец, тем относительное его удлинение больше и тем сильнее сказывается появление на нем «шейки» при растяжении. Одновременно с появлением шейки возникает и растет составляющая напряжения среза. Образец не имеет одинакового напряжения по сечениям, нормальным к на­правлению растягивающей силы. Разрыв начинается там, где снаружи или внутри образца было раньше какое-либо ослаблен­ное место (надрезы, трещины, полости); затем такой разрыв раз­растается и приводит к вазвушению образца.
струкции, работающие на растяжение, мало употребительны (характерное исключение составляют амортизационные шну­ры).

Сжатие. Конструкции, в которых резина подвергается одно­осному статическому или динамическому сжатию, находят более широкое применение. Сжатие образца резины при одноосном нагружении, проводимое между двумя параллельными плитами, мо­жет осуществляться в двух различных условиях: со смазкой или без смазки опорных поверхностей. Так как трение опорных поверх­ностей образца по плитам препятствует свободному расширению образца в боковом направлении, то боковая поверхность частично изгибается и приходит в контакт с плитами.

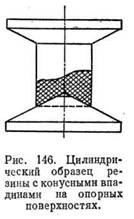
Применяя смазку опорных поверхностей и плит, можно облегчить скольжение образца по плитам. В этом случае, даже до значитель­ного уменьшения высоты, образец все же сохраняет форму цилиндра. То же происхо­дит в случае применения цилиндрических об­разцов с конусными впадинами на опорных поверхностях (рис. 146). Некоторую ана­логию сжатия без трения можно видеть на примере уменьшения толщины тонкостенного резинового надувного шара (шара пилота), растягиваемого внутренним давлением газа. Подобное этому напряженное состояние можно наблюдать при двуосном растяжении тонких крестообразных образцов резины.

Экспериментальная кривая зависимости f— е сжатия, в отличие от кривой при рас­тяжении, монотонна. Эту кривую Ариано принимал за равнобокую гиперболу с асимптотами, параллельными осям напряжений и деформаций.

Действительно, при растяжении стенок резинового полого шара, когда диаметр шара увеличивается, например до семикратного размера, толщина стенки уменьшается до 0,02 начальной, что дает а = —0,98. Если в уравнении (8.11) принять а = —1, то приходим к уравнению (8.5) с Е = С. Для а = fл уравнение (8.11) линейно. Напряжение f (или o) имеет знак минус.

Линейная зависимость по уравнению (8.4) сохраняется и для случаев равновесного и статического сжатия резины с применением смазки; сохраняется зависимость и по уравнению (8.5).

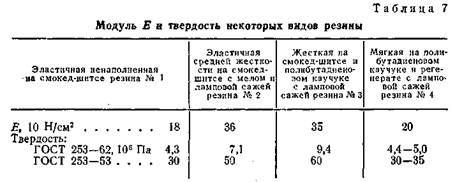
Величины значений Е для некоторых производственных резин приведены в табл. 7.

Данные табл. 7 были получены при исследовании на сжатие образцов резины со смазкой их опорных поверхностей. Исследова­лись шесть видов круговых ре­зиновых цилиндров диаметром 31 мм и высотой от 38 до 5 мм и три вида образцов цилин­дрических резиновых колец наружным диаметром 31 мм, внутренним — 14,7 мм и высо­той от 11 до 5 мм. Сжатие производилось в равноскоростной деформации до Я, в преде­лах 0,90—0,50 с замерами че­рез 1 мин после приложения последовательно возраставшей нагрузки.

Несмотря на значительное различие габаритов исследо­ванных образцов, ширина пуч­ка зависимости f—л незначи­тельна, и разброс эксперимен­тальных значений, по сравне­нию с рассчитанными по урав­нению (8.5), невелик.

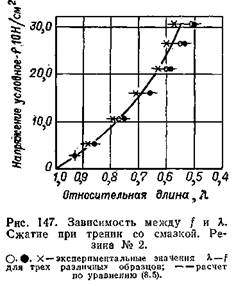
На рис. 147 приведены экспериментальные и расчетные значе­ния л по заданным f для трех различных видов цилиндрических образцов из исследованной серии. Как уже было замечено, явле­ние сжатия при сухом трении более сложно. Цилиндрический об­разец резины, подвергаемый одноосному нагружению между двумя сухими плитами пресса, испытывает (в направлении, перпендику­лярном нагружению) двухосное растяжение, а по плитам и вблизи них, вследствие возникновения трения — сдвиг. Совместный эффект сжатия, двухосного растяжения и сдвига ведет к изгибу (выпучи­ванию) боковой поверхности образца. Вертикальная ось сохраняет свое положение, но лишь при условии ограниченной высоты об­разца, например в отношении h₀: do = 1,5. В образцах большой высоты наблюдается продольный изгиб и образец, теряя устойчи­вость, иногда выскакивает из междуплитного пространства. Наи­большее напряжение растяжения создается в сечении, лежащем посредине высоты образца на его периферии. В центре опорных поверхностей образец частично испытывает трехосное сжатие.

Читайте также: Где производят шины кумхо летние

Видео:Покрышка с деформациейСкачать

Нахождение расчетной зависимости напряжение — деформация cжатия при сухом трении затрудняется из-за неоднородности распределения нормальных напряжений и возникающего объемного напряжения, связанного с формой и габаритами образца. Исследо­вание распределения нормальных напряжений резины с учетом трения могло бы дать правильное понимание явления, но оно еще недостаточно изучено. В обход этого затруднения, для практиче­ской оценки поведения резины при сжатии, условно заменяют слож­ное напряженное состояние простым сжатием с учетом формы образца.

В качестве условного обобщающего измерителя влияния формы принимают коэффициент формы Ф. Коэффициент Ф понимают как отношение опорной поверхности образца к той или иной части ее, обычно к полной боковой поверхности. Отсюда для круговых ци­линдров Ф имеет следующее значение

где d1 и d₂ — внутренний и наружный диаметры цилиндра; h₀ и b — высота и толщина стенки цилиндра.

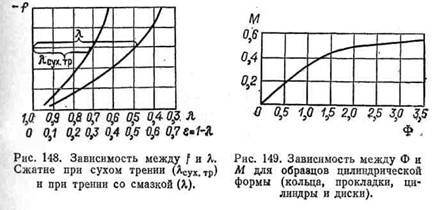
Для решения подобных задач может быть принят такой общий метод. Допускается (рис. 148), что при равных напряжениях f между величиной относительной высоты образца при сжатии в ус­ловиях сухого трения Л_cvx. тр и величиной относительной его вы­соты л при сжатии со смазкой есть достаточно постоянная зависи­мость, выражаемая коэффициентом затрудненности скольжения М;

Этот коэффициент для серии однотипных, но разногабаритных образцов можно найти экспериментально и связать его с коэффи­циентом формы Ф в табличной или графической зависимости.

Из уравнения (8.13) находят относительную высоту л образца, сжимаемого при трении со смаз­кой

Теперь от уравнения (8.5) сжатия при трении со смазкой можно перейти к уравнению сжа­тия при сухом трении. Для этого в уравнении (8.5) достаточно за­менить % ее обозначением из уравнения (8.13′)

На рис. 149 дана зависимость М от Ф для ряда массивных и полых цилинд­ров и дисков с коэффициентом формы 0,20—3,25.

Как видно из рис. 149, зависимость М от Ф нелинейна и отвечает двум кри­вым, переходящим одна в другую при Ф = 1,35, Эти кривые достаточно близко описываются следующими уравнениями:

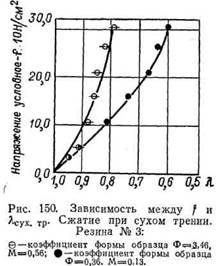
Графическое сопоставление расчетных и экспериментальных значений Л_сух. тр по заданным напряжениям f для двух видов об­разцов дано на рис. 150. Для круговых цилиндров из ненаполненной резины при сжатии без смазки линейность зависимости о и е приводит к следующему уравнению;

где Есж.к — условно принимаемый модуль сжатия конструкции по истинному напряжению, зависящий, как и статический модуль сжа­тия Е резины, от характера деформации, а также от габаритов образца и условий на опорных поверхностях; а — постоянная, зависящая от трения по опорным поверхностям.

Здесь а приближенно равна удвоенному коэффициенту трения М_T резины по металлу, из которого изготовлены сжимающие плиты; удвоение М_T отвечает количеству трущихся пар.

При наличии надлежащей смазки, когда а может быть при­нята близкой к нулю, Е_сж._к независимо от величины Ф становится равным Е. С увеличением Ф значительно возрастает и Есж.к. Для случая прочного крепления опорных поверхностей образца резины к металлическим прокладкам а, независимо от коэффициента Ф, может быть принято равным 4,67. Наличие «выкружки» по боко­вой поверхности может вести к устранению бочкообразности.

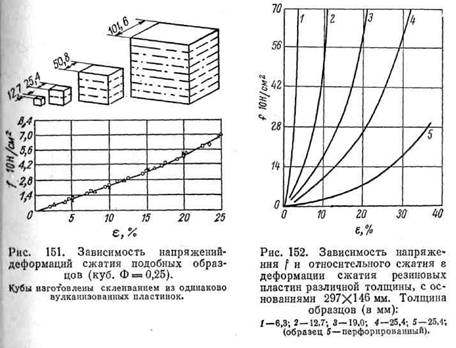
При постоянстве Ф уравнение (8.16) показывает возможность моделирования: точки зависимости f и е для геометрически подоб­ных образцов из одной и той же резины хорошо ложатся на одну кривую (рис. 151). Однако при значительных деформациях, или для образцов больших размеров, или же сложных конфигура­ций, названные зависимости недостаточны.

В зависимости от особенностей формы, наличия отверстий или ребер в резиновых пластинах жесткость их, являющаяся очень важной технической характеристикой, может быть различной.

На рис. 152 приведена зависимость между условным напряжс нием сжатия f и относительным сжатием (осадкой) е для пластин, имеющих одинаковые опорные поверхности, но различную тол щину (высоту). По мере увеличения толщины (иначе — с уменьше­нием коэффициента формы) относительное сжатие возрастает, жесткость уменьшается, резиновая пластина становится «мягче». При наличии отверстий или пор в пластинах это сказывается более значительно (кривая 5 на рис. 152). С уменьшением же толщины пластина становится жестче. Применение смазки, нивелируя влияние коэффициента формы Ф, приводит к объемлющей кривой, лежащей ниже кривой 4 (а возможно и кривой 5).

Примером резиновых изделий, работающих на сжатие, являют­ся уплотнительные прокладки и амортизаторы.

Видео:ТИХИЕ ШИНЫ ЭТОГО НЕ ЗНАЮТ БОЛЬШИНСТВО АВТОМОБИЛИСТОВСкачать

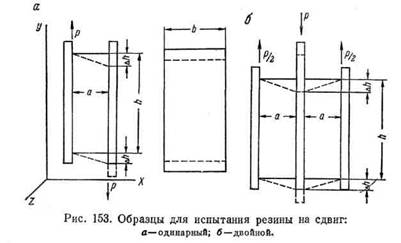
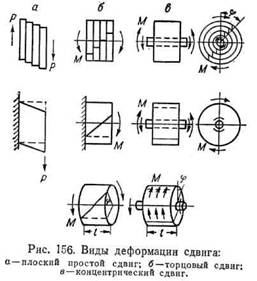
Сдвиг. В практических условиях работы резины при так назы­ваемом простом (плоском) сдвиге (рис. 153, а) напряжение сдвига т приложено на двух параллельных сторонах образца резины, к ко­торым привулканизована металлическая арматура. Отношение смещения Аh к начальной толщине образца а представляет собой относительный сдвиг у. Поскольку площадь плоскости сдвига по­стоянна, понятия условного и истинного напряжений сдвига т со­впадают. Материальной константой зависимости т и у является модуль сдвига G, зависящий от характера деформации резины

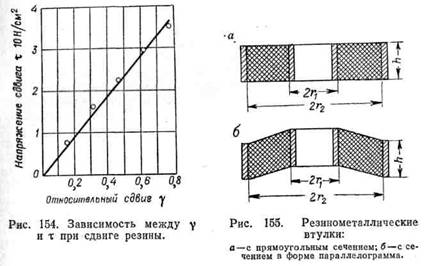
Графическая зависимость т и у (рис. 154) при деформации сдвига малонаполненных резин до у порядка 0,7—0,8 практически линейна. Осевое растяжение может заметно сказаться и осложнить эту зависимость в том случае, если размер а превышает 0,25 h₀. При сдвиге в образце одновременно проявляются: растяжение по одной из диагоналей и сжатие по другой. При этом относительные деформации диагоналей е меньше относительного сдвига у. Кроме напряжения сдвига т резиновый блок испытывает и нор­мальное напряжение растяжения по оси у (рис. 153):

Это нормальное напряжение, будучи пропорциональным квад­рату относительного сдвига, незначительно лишь тогда, когда сдвиг мал, но становится существенным при его большой величине. По оси z нормальное напряжение может быть принято равным нулю. В конструкциях цилиндрических резиновых втулок (рис. 155) пло­ский сдвиг обращается в круговой. Напряжение в круговом сдвиге прямоугольной резиновой втулки при малой деформации:

Максимальное его значение отвечает внутренней поверхности резинового массива. Осевое смещение Ah в круговом сдвиге состав­ляет:

Для конструктора, относящего расчетные напряжения к началь­ным площадям нагружаемых сечений, важно относительное по­стоянство модуля сдвига G, по сравнению с переменным и возрастающим дифференциальным модулем сжатия Ef. Суще­ственно также и то, что модуль сдвига втрое ниже модуля сжатия. Размеры и формы монолитных образцов резины, прочно (полно­стью) прикрепленных к металлической базе, практически не влияют на модуль сдвига конструкции, тогда как габариты и вид образцов, работающих на сжатие, значительно сказываются на модуле сжа­тия конструкции.

Модуль сдвига в приближенной зависимости от твердости ре­зины характеризуется следующими данными:

Практические пределы G для производственных резин состав­ляют (3,5—20) -10 Н/см 2 .

На сдвиг работают многие резиновые конструкции, в частности пластинчатые амортизаторы. Максимально допустимое т состав­ляет (3,9—4,2)-10 Н/см 2 , а в тяжелых условиях дина­мических режимов даже (2,1— 2,4). 10 Н/см 2 , а макси­мальное у не должно пре­вышать 0,5.

Кручение. Различают два вида скручивания резины: торцовое и концентрическое. Эти виды кручения можно рассматривать как явление торцового и концентриче­ского сдвигов. Последний наблюдается в резиновых втулках (рис. 156), заключенных между двумя метал­лическими деталями (так называемых бесшумных блоках).

Расчетная зависимость полного углового смещения ф в радианах и крутящего момента М торцового кручения при ма­лых деформациях определяется уравнением

В случае рассматриваемого торцового кручения резины, кроме Касательного напряжения т, имеется нормальное f_z по свободной торцовой поверхности (по оси z). Это нормальное напряжение цвисит от квадрата величины углового смещения ф/l, неоднородно и распределено по торцовой поверхности по параболическому за­кону:

Угловое смещение при концентрическом кручении цилиндриче­ских резиновых прямоугольных втулок при малых деформациях определяется следующим уравнением:

и достигает максимума по внутренней поверхности втулки. Пример резиновых изделий, работающих на кручение, — демпфер крутиль­ных колебаний коленчатого вала.

Изгиб. При значительном изгибе гибких металлических дета­лей— тонких полос и стержней, имеющих (вследствие малой вели­чины их момента инерции I) малую изгибную жесткость EI,— неприменимо известное упрощенное уравнение упругой линии:

Читайте также: Как заклеить дырку в шине велосипеда

Видео:Об этом никто не знает! Как узнать высоту шины автомобиля!Скачать

Для этого случая Е. П. Поповым подробно разработана теория изгиба, позволяющая вести расчет брусьев малой жесткости в случае любых больших прогибов и перемещений точки приложе­ния нагрузки. Для практического применения общих решений этой теории им дан графоаналитический метод расчета по диаграммам упругих параметров и таблицам для построения этих диаграмм.

Теория расчета изгиба при больших перемещениях представляет интерес и для исследования изгиба резиновых и резино-текстильных слойных конструкций. В этих случаях, вследствие малой неличины модуля Е, условная жесткость их EI также мала. Такие изделия могут иметь значительный прогиб, а при консольном нагружении их также и со значительным смещением точки приложения нагрузки.

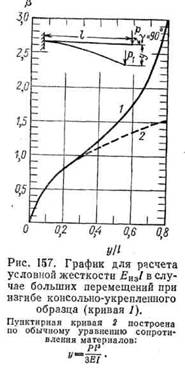
Исходя из таблиц и уравнений упругих параметров Е. П. Попова, могут быть даны графические построения для расчета эффективного модуля изгиба таких конструкций в частных задачах, соответствующих нагружению консоли и кольца.

Кривая 1 рис. 157, соответствующая нагружению по приведен­ной на рисунке схеме, позволяет по экспериментально определен­ному отношению прогиба консоли у к длине I найти величину в, так называемый силовой коэффициент подобия. Зная в, можно по заданным нагрузке Р, длине l и моменту инерции I из уравнения

вычислить Е_из— материальную характеристику изгибоспособноети конструкции (эффективный модуль при изгибе) и условную при изгибе жесткость конструкции Еиз1 (принимая ее в пределах экспери­мента постоянной).

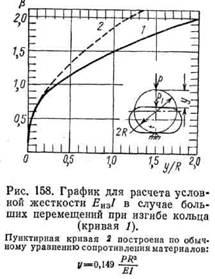
Кривая 1 рис. 158, отвечающая нагружению по приведенной на рисунке схеме, позволяет найти в как функцию отношения y/R. Аналогично уравнению (8.27), но заменив в нем l на R, а Р на 0,5 Р, можно найти Е_из. Пунктирные линии на рис. 157 и 158 соот­ветствуют зависимости, вытекающей из обычных уравнений сопро­тивления материалов. Нагружение по схеме изгиба консоли рис. 157 удобно для исследования изгиба резино-текстильных пла­стин. По схеме рис. 158 ведут исследования радиального прогиба резины, имеющей форму кольца прямоугольного сечения среднего радиуса R, или резино-текстильной полоски, свертываемой в такое кольцо. Если применяется схема рис. 158, El следует заменять ци­линдрической жесткостью:

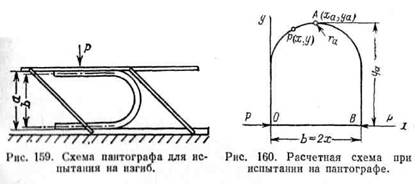
Метод экспериментального определения жесткости при изгибе, удобно при­менимый для резино-текстильных изделий (плоских и клиновых ремней, рукавов, технической пластины), предложен Штекертом. Прямой участок испытывае­мого изделия изгибают U-образно по схеме рис. 159 в приспособлении, состоя­щем из двух параллельных планок пантографа. Усилие Р (в ЮН) и расстояния а (в см) измеряют; расстояние между ней­тральными поверхностями Ь (в см) рассчи­тывают, исходя из геометрических размеров поперечного сечения исследуемого изделия. Из теоретических положений, следуя схеме обозначений на рис. 160, Штекертом найдены следующие зависимости:

Следует доводить изгиб до кривизны, отвечающей условиям эксплуатации, так как жесткость El зависит от величины изгиба изделия. Замеры следует про­изводить через определенные промежутки времени после приложения нагрузки, например через 30 с. Перегибать изделия до «залома» не следует.

Сложные виды деформаций. Основные виды деформации — растяжение, сжатие, сдвиг и кручение — в реальных конструкциях резиновых деталей осложняются взаимным наложением в различ­ных комбинациях, что приводит к сложным видам деформаций, например вдавливанию. Обычно сжатие сопровождается сдвигом, а иногда — кручением. Результат комбинированных нагружений выражается в изменении характера кривых на диаграммах зави­симости условное напряжение — деформация конструкции. В от­дельных случаях зависимость принимает линейный характер. Од­нако необходимо учитывать, что отношение напряжения к дефор­мации в линейной их зависимости представляет собой модуль лишь при упругой деформации. Условием этого можно считать, что деформации при последующей разгрузке вполне или в значи­тельной степени, например на 90—95%, обратимы.

Двухосное растяжение резины, являющееся аналогом чистого одноосного сжатия, было предметом ряда исследований . Модуль резины при двухосном растяжении для равновесной деформации, при растяжении 10—100%, в 1,57 раза выше модуля одноосного растяжения. Случай чистого двухосного сжа­тия не исследован. Более доступен для изучения относительно близкий к нему случай одноосного удлинения резины, сжимаемой в канале заданной ширины. Поскольку при такой деформации значительно проявляется объемное напряжение, коэффициент за­трудненности скольжения М получает иное значение, зависящее от габаритов и конфигурации канала и длины образца.

Трехосное растяжение резины практически неосуществимо; тео­ретически такой случай близок к свободному набуханию резины в подходящей жидкости. Трехосное сжатие, например, представ­ляет собой случай осевого нагружения резиновой прокладки в же­стком гнезде с размерами, равными наружным размерам образца. В подобных условиях резина, не имея возможности деформации по двум остальным осям, ведет себя как малосжимаемый материал. Модуль резины при трехосном сжатии, или так называемый объем­ный модуль, весьма значителен [около (2,7—3,8) -10 Н/см 2 ].

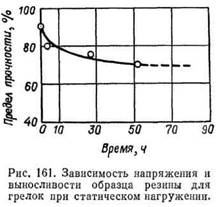
Усталость резины. В зависимости от особенностей назна­чения резиновые детали подвергаются различным условиям дли­тельного нагружения. Длительное приложение нагрузки ведет к усталости материала. Способность материала сопротивляться усталости — выносливость — может быть определена длительностью в зависимости от величины нагружения и величины деформации. Применение длительных статических нагрузок встречается при ис­пользовании резины в качестве уплотнительных прокладок в не­подвижных узлах. Находящийся в длительном статическом нагру-жении постоянным грузом (даже значительно меньшим «мгно­венно» разрушающего) образец резины все же разорвется. Разрыв наступит за время, тем более короткое, чем больше нагружен обра­зец. Эта статическая усталость проявляется как в массе исследуе­мого образца резины, так и в тонком слое, соединяющем, напри­мер, резину с металлической арматурой. Ближайшей причиной разрушения при статической усталости, как уже указывалось, яв­ляется наличие в материале беспорядочно размещенных относи­тельно слабых мест и надрывов, вызывающих концентрацию на­пряжений или связанных с значительными местными отклонениями в свойствах материала.

Резина, по сравнению со сталью, способна вынести деформации во много раз больше, так как пределы (хотя и несовершенной) уп­ругости и прочности резины практически совпадают. При этом, если рабочие деформации растяжения не превышают 10% от деформа­ций, происходящих при разрушении образца, то после прекращения действия деформирующих усилий образец резины почти полностью возвращается в исходное состояние и принимает свои прежние раз­меры.

Разрыв под влиянием статической усталости иногда происхо­дит внезапно, без предшествующего указания на близкое разруше­ние. Зависимость приложенного условного напряжения и длитель­ность сопротивления разрыву следуют кривой, асимптотически приближающейся к оси абсцисс. Разные типы резины при испыта­нии в одинаковых условиях дают различные результаты. Пре­дельно допустимым в рассмотренном нами случае (рис. 161) (ре­зина для грелок) является для f 70% от предела прочности резины на разрыв. В логарифмических координатах эта зависимость ли­нейна. Чаще, однако, резина работает в периодических, динами­ческих (шины, амортизаторы, уплотнители подвижных узлов) или ударных (буферы) режимах нагружения.

Динамические режимы могут быть различны по виду нагруз­ки (циклическая, переменная, пульсирующая и др.) и по частоте, а следовательно, различны и по длительности приложения нагруз­ки. В том случае, когда эта дли­тельность приближается ко вре­мени, необходимому для релак­сации напряжения, последнее, замеряемое в конце цикла дефор­мации, близко к равновесному. Чем меньше длительность прило­жения нагрузки, тем замеряемое напряжение ближе к начально приложенному. Сопротивление резины динамическому утомле­нию (проявлению динамиче­ской усталости) зависит от потерь на внутреннее трение. При значительном напряжении в этом сопротивлении преобладает физический фактор — прочность резины. При малом напряжении и отвечающей ему длительности сопротивления существенное зна­чение имеет химическая стойкость резины. Уменьшение внутрен­него трения, наблюдающееся, например, при набухании, снижает интенсивность хода химических реакций и ведет к увеличению динамического сопротивления.

Выносливость к многократным деформациям резиновых изде­лий зависит не только от вида резины и характера деформаций, но в большей степени от размеров и конфигурации деталей, а также от характера цикла (т. е. от условий нагружения). Предел усталости в знакопостоянном цикле меньше, чем в знакоперемен­ном (ср. 2 и 1 на рис. 109). Отсюда усталостное поведение резины в образцах в условиях лабораторных испытаний нельзя, безотно­сительно к конкретным условиям работы изделий, распространять на поведение резины в эксплуатации.

При расчетах резины в динамических циклах рекомендации сво­дятся главным образом к установлению эмпирической зависимости между напряжением или деформацией и количеством циклов де­формации, перенесенных образцом до разрушения или до опреде­ленной величины потери начальных прочностных свойств. Более широко применяются расчеты резины как виброизолирующего средства.

• Свежие записи
  • Нужно ли менять пружины при замене амортизаторов
  • Скрипят амортизаторы на машине что делать
  • Из чего состоит стойка амортизатора передняя
  • Чем стянуть пружину амортизатора без стяжек
  • Для чего нужны амортизаторы в автомобиле

  
  

  источники:

  Видео:устраняем биение шиныСкачать

  

  https://fasad-adelante.ru/kak-rasschitat-deformatsiyu-shiny

  📹 Видео

  Дефекты автомобильных шин - что бывает при неправильной эксплуатации и как этого избежать.Скачать

  

  Всего за 2 минуты определить направление движения у колеса, если нет Никаких ОбозначенийСкачать

  

  Как понять, когда протектор износился и шины пора менятьСкачать

  

  Биение руля на малой скорости или вибрация кузова при разгоне ? 90 Кривое колесо на машинеСкачать

  

  Жёсткость шины и высота профиля. Размеры шин. Как выбрать.Скачать

  

  ОБ ЭТОМ МНОГИЕ ДАЖЕ НЕ ДОГАДЫВАЮТСЯСкачать

  

  Как определить беговую грыжу колеса на автомобиле своими рукамиСкачать

  

  Деформация колеса на скоростиСкачать

  

  Как определить стоит ли брать резину на авто?Скачать

  

  Как определить износ резины?Скачать

  

  Как читать размер шин 🛞Скачать

  

  Диаметр шины. Как измерять диаметр шины?Скачать

  

  8ка или нет?! И как определить ровность колеса.Скачать

  

  ШИРИНА ШИНЫ, КАК ПОДОБРАТЬ ШИНЫ ПО ШИРИНЕ ДИСКА?Скачать