Как рассчитать цилиндр из листа (3 видео)

Содержание

Простейший расчет и производство цилиндрических емкостей из пластиковых листов
2 Производство емкости
2.1 Изготовление цилиндра
Таблица 2 Допустимая деформация различных материалов
2.2 Приварка дна
Развертка цилиндра
Развертка цилиндра для склеивания
Калькулятор развертки усеченного плоскостью цилиндра онлайн
Обозначения
Введите радиус или диаметр *:
Введите высоты * и (или) угол:
Округление:
Построение развёртки:
Графики
Формулы
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Развертка прямого кругового цилиндра.
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
Развертка усеченного цилиндра.
📺 Видео

Видео:Цилиндр - расчёт площади, объёма.Скачать

Простейший расчет и производство цилиндрических емкостей из пластиковых листов

Видео:Как сделать ИДЕАЛЬНЫЙ цилиндр из бумагиСкачать

2 Производство емкости

Видео:Простой расчёт развёртки конусаСкачать

2.1 Изготовление цилиндра

Первым этапом производства цилиндрической емкости из листового пластика является сварка цилиндра, образующего стенки емкости. Для этого лист насильно сворачивается в трубу без какого-либо нагрева или применения растворителей, и его противоположные грани свариваются между собой. С учетом фактора сварки, лучше всего это делать методом стыковой сварки нагретым инструментом (рис.4). Оборудование для этого метода сварки – см. здесь.


Рис.4 Сварка трубы из пластикового листа

При сворачивании пластикового листа важно не превысить максимально допустимой деформации, в противном случае в материале возникают зоны ползучести материала или трещины. Максимально допустимая деформация измеряется в процентах и позволяет рассчитать минимально допустимый радиус скругления для листа любой толщины. DVS 2205-1 рекомендует предельно допустимые значения деформации согласно табл.2.

Видео:Объём цилиндраСкачать

Таблица 2 Допустимая деформация различных материалов

Видео:Котика ударило током, 10 т. ВольтСкачать

2.2 Приварка дна


Рис.5 Сварка горячим воздухом	Рис.6 Экструзионная сварка

Оборудование для сварки горячим воздухом можно посмотреть здесь.
Для экструзионной сварки – здесь.

Дно приваривается одним из вариантов швов, показанных на рис.7-9. Величина b в каждом из вариантов зависит от того, планируется ли якорное крепление дна емкости к полу:

Видео:Как легко сделать усеченный конус (конус) из металла 2 мм. Сделай сам!Скачать

Развертка цилиндра

Для того, что-бы сразу получить готовую развертку цилиндра, кликните по ссылке.
Для получения готовой развертки наклонного цилиндра, кликните по этой ссылке.
Если нужна развертка конуса, то переходите сюда.
Для получения развертки усеченного конуса, переходите сюда..

Если же Вас интересует вопрос, как сделать развертку цилиндра самостоятельно, без использования калькулятора разверток, то следующая статья для Вас.

Читайте также: Как изобразить осевое сечение цилиндра

Видео:Видеоурок по математике "Цилиндр"Скачать

Развертка цилиндра для склеивания

Цилиндр — простая геометрическая фигура, представляющая из себя вытянутое тело, ограниченное с обоих сторон двумя плоскостями (основаниями).
Для простоты представления, прямая труба — это цилиндр.
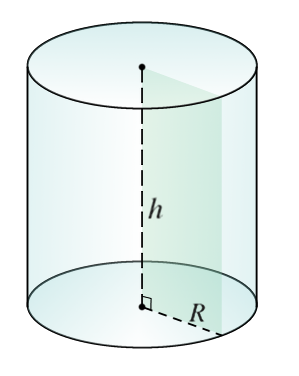
На рисунке 1 изображен прямой круговой цилиндр. Прямой — означает, что угол между осью цилиндра и плоскостью основания — прямой (равен 90 град.), круговой — означает, что в основании цилиндра лежит круг.

Для построения развертки прямого кругового цилиндра потребуются две величины: 1) высота цилиндра (H), 2) диаметр круга, который лежит в основании (D),

Цилиндр может быть не круговым. Например на рисунке 2 изображен овальный цилиндр. Овальный — означает, что в основании цилиндра лежит овал.

Также, цилиндр может быть не прямым, а наклонным. У наклонного цилиндра (меньше 90 град.). На рисунке 3 изображен наклонный цилиндр.

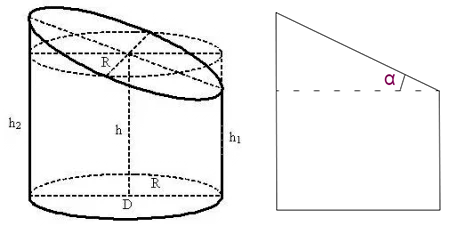
Для построения развертки наклонного цилиндра потребуются три размера: 1) высота цилиндра (H), 2) радиус окружности (R), 3) угол наклона оси (A), Перейти к построению.

Видео:Построение развертки цилиндра. Урок 37.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Калькулятор развертки усеченного плоскостью цилиндра онлайн

Видео:Как сделать цилиндр из бумаги.Скачать

Обозначения

R — радиус основания цилиндра;
D — диаметр основания цилиндра;
h — средняя высота усечённого цилиндра;
h1 — наименьшая высота усечённого цилиндра;
h2 — наибольшая высота усечённого цилиндра;
α — угол сечения, град.
X_{1 .. n} — координаты для построения развёртки по оси X;
Y_{1 .. n} — координаты для построения развёртки по оси Y;

Числовые значения в таблице заполняются числом (5; 5.16; -3.12), либо математическим выражением (5/7; (1-5)*2.13)

Введите радиус или диаметр *:

Введите высоты * и (или) угол:

Без макс. и мин. высоты можно посчитать только площади боковой поверхности и основания и объём

Или введите одну из высот и угол сечения (рис.)

Округление:

Построение развёртки:

Видео:КАК СДЕЛАТЬ ЦИЛИНДР ИЗ БУМАГИ? КАК СДЕЛАТЬ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ? ГЕОМЕТРИЧЕСКИЕ ТЕЛА. | #RAIDOTVСкачать

Графики

Чертится развертка усеченного плоскостью цилиндра, как показано на рисунке:

Видео:Уроки Solidworks.Развёртка цилиндраСкачать

Формулы

Формула для вычисления значений Y:

Y_i = D * tg(α) * sin (i * (180 / n)) , здесь: i — номер точки, α — угол сечения, n — количество точек развертки, D — диаметр цилиндра;

Формула для вычисления значений X:

X_i = ((π * R 2 ) / n) * i , здесь: i — номер точки, α — угол сечения, n — количество точек развертки, R — радиус цилиндра, π — число Пи (прим. 3.14);

Читайте также: Устройство тормозного цилиндра ниссан

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.

Видео:развертка конусаСкачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.

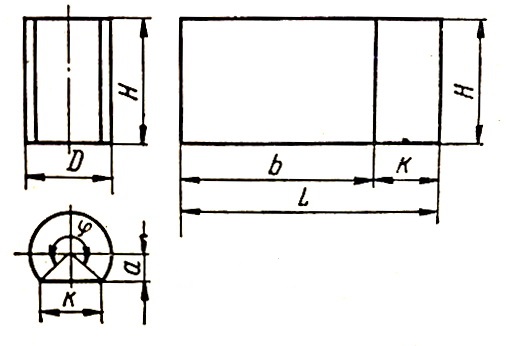
Развертка прямого кругового цилиндра.

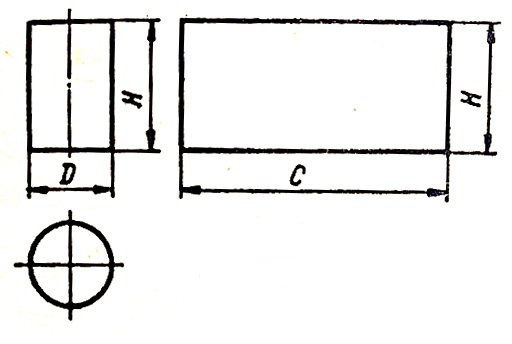
Цилиндр диаметром D и высотой H показан на рис. 1. Развертка представляет собой прямоугольник длиной с = πD и высотой Н.

Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2) 2 – a 2 ) = 2a tg (ᵠ/2).

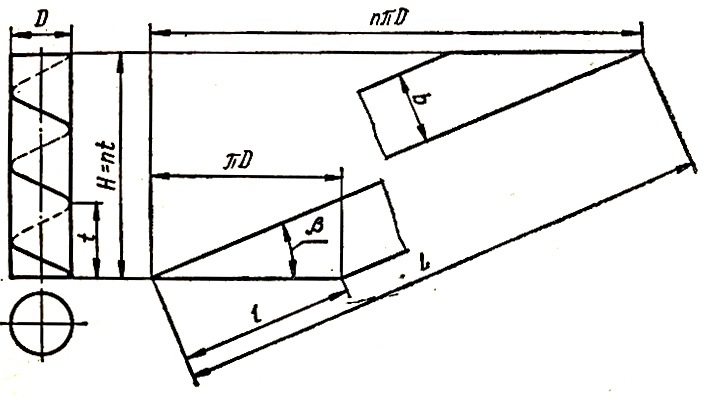
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.

Цилиндр показан на рис. 3. При определении развертки можно использовать следующие зависимости:

n — число полных витков на общей длине цилиндра H, Н = nt;

Развертка усеченного цилиндра.

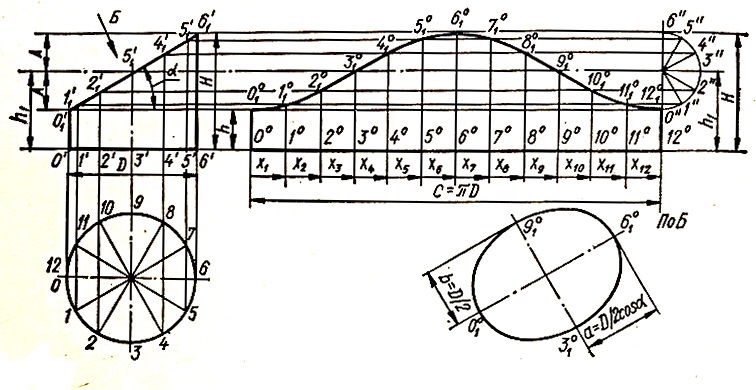
Для получения развертки горизонтальная проекция цилиндра делится на равные части и точки деления нумеруются (в данном случае от 0 до 12). Из точек деления проводятся вертикали до пересечения верхнего основания в точках 0′₁, 1′₁…, 6′₁. На продолжении прямой 0’6′ откладывается отрезок длиной с = πD, который делится на принятое число равных частей. Из точек деления 0₀, 1₀, …, 6₀ строятся перпендикуляры до их пересечения с соответствующими горизонтальными линиями в точках 0 0 ₁, 1 0 ₁, …, 6 0 ₁. Полученные точки соединяются плавной кривой. Ввиду симметричности остальные точки кривой находит аналогичным путем.

Линию развертки можно определить и таким способом. На расстоянии h1 = (h + H)/2 от линии 0 0 12 0 проводится параллельная прямая. Из центра S, лежащего на прямой, описывается полуокружность радиусом А. Полуокружность делится на равные части, число которых равно половине точек деления развертки (в данном случае на шесть). Через точки деления 0ꞋꞋ, 1ꞋꞋ, …, 6ꞋꞋ проводятся горизонтальные прямые до пересечения вертикалей, проходящих через 0 0 , 1 0 , … , 12 0 . Полученные точки 0 0 ₁, 1 0 ₁, …, 12 0 ₁ соединяются плавной кривой.

Верхнее основание цилиндра представляет собой эллипс с полуосями a = D/2 cos α = 0′₁3′₁ и b = D/2.

При аналитическом определении координат точек кривой развертки цилиндра, усеченного плоскостью под углом α (рис. 5), могут быть использованы следующие зависимости:

x_k = kx₁ = πD/2 kε/180°; y_k = D/2 tg α sin kε = A sin kε = A sin ᵠ_i,

где х₁ = πD/ (2n) = πD/2 ε/180° — длина дуги окружности основания цилиндра, разделенная на 2n равных частей; ε = 360°/2n — центральный угол, соответствующий одному делению; k — порядковый номер точки; A = (H — h)/2 = (D/2) tg α — амплитуда синусоиды; ᵠ_i= kε.

Читайте также: Цилиндр во всех плоскостях изометрии

Значения sin kε для наиболее часто употребляемых значений 2n приведены в табл. 1.

Таблица 1. Значения sin kε и sin 2 kε

2n				sin kε	sin 2 kε	2n				sin kε	sin 2 kε
8	16	32	64	sin kε	sin 2 kε	12	24	48	96	sin kε	sin 2 kε
—	—	—	1	0,09802	0,00961	—	—	—	1	0,06540	0,00428
—	—	1	2	0,19509	0,03806	—	—	1	2	0,13053	0,01704
—	—	—	3	0,29028	0,08426	—	—	—	3	0,19509	0,03806
—	1	2	4	0,38268	0,14645	—	1	2	4	0,25882	0,06699
—	—	—	5	0,47139	0,22221	—	—	—	5	0,32144	0,10332
—	—	3	6	0,55557	0,30866	—	—	3	6	0,38268	0,14645
—	—	—	7	0,63439	0,40245	—	—	—	7	0,44229	0,19562
1	2	4	8	0,70711	0,50000	1	2	4	8	0,50000	0,25000
—	—	—	9	0,77301	0,59754	—	—	—	9	0,55557	0,30866
—	—	5	10	0,83147	0,69134	—	—	5	10	0,60876	0,37059
—	—	—	11	0,88192	0,77778	—	—	—	11	0,65935	0,43474
—	3	6	12	0,92388	0,85355	—	3	6	12	0,70711	0,50000
—	—	—	13	0,95694	0,91573	—	—	—	13	0,75184	0,56526
—	—	7	14	0,98079	0,96194	—	—	7	14	0,79335	0,62941
—	—	—	15	0,99518	0,99039	—	—	—	15	0,83147	0,69134
2	4	8	16	1,00000	1,00000	2	4	8	16	0,86617	0,75000
—	—	—	17	0,89687	0,80438
—	—	9	18	0,92388	0,85355
—	—	—	19	0,94693	0,89668
—	5	10	20	0,96600	0,93301
—	—	—	21	0,98079	0,96194
—	—	11	22	0,99144	0,98296
—	—	—	23	0,99786	0,99572
3	6	12	24	1,00000	1,00000

Примечание: Значения sin kε и sin 2 kε даны для одной четверти окружности. В остальных четвертях они повторяются.

Ввиду симметричности синусоиды достаточно определить координаты точек одной четверти окружности, например от у₀ до у₃. Остальные координаты имеют соответственно равные значения. Например: у₄ — у₂, …, у₁₁ = — у₁ и т. д.