- Как сделать развертку цилиндра начертательная геометрия
- Как сделать развертку цилиндра начертательная геометрия
- Развертка поверхности цилиндра в начертательной геометрии с примером
- Развертка поверхности цилиндра:
- Развертка цилиндра
- Алгоритм построения развертки цилиндра
- Видео «Развертка цилиндра»
- ПОСТРОЕНИЕ РАЗВЕРТОК ПОВЕРХНОСТЕЙ Методические рекомендации по курсу начертательной геометрии
- Бийский технологический институт (филиал)
- Г.И. Куничан, Л.И. Идт
- ПОСТРОЕНИЕ РАЗВЕРТОК
- ПОВЕРХНОСТЕЙ
- Методические рекомендации по курсу начертательной геометрии
- Куничан Г.И., Идт Л.И . Построение разверток поверхностей:
- Методические рекомендации по курсу начертательной геометрии для самостоятельной работы студентов механических специальностей 171200, 120100, 171500, 170600.
- ОБЩИЕ ПОНЯТИЯ О РАЗВЕРТЫВАНИИ ПОВЕРХНОСТЕЙ
- 🔍 Видео
Видео:[Начертательная геометрия] Развертка цилиндра или как сделать развертку цилиндраСкачать
![[Начертательная геометрия] Развертка цилиндра или как сделать развертку цилиндра](https://i.ytimg.com/vi/Gh2jo9L_8gs/0.jpg)
Как сделать развертку цилиндра начертательная геометрия
Контрольные задания по теме:
Рабочая тетрадь задача 68, задача 69
Цилиндром будет называться геометрическое тело, полученное при ограничении цилиндрической поверхности двумя параллельными плоскостями — основаниями цилиндра. Если в основании цилиндра лежит окружность, а образующая перпендикулярна основанию, то цилиндр называется прямым круговым.
Линия сечения строится также при помощи опорных точек — точек пересечения секущей плоскости с очерковыми образующими и осью цилиндра. Но необходимо взять также промежуточные точки для более точного построения линии сечения. На рисунке 49 показано построение проекций сечения цилиндра фронтально — проецирующей плоскостью S. Так как цилиндр является проецирующей поверхностью, то горизонтальная проекция сечения совпадает с секущей плоскостью и на профильной проекции получим эллипс. Точки 2 и 3 будут являться границей видимости линии сечения для профильной плоскости.
Натуральную величину сечения можно определить способом вращения. Ось вращения выбираем в точке 1 и вращаем секущую плоскость до положения, параллельного горизонтальной плоскости. На горизонтальной плоскости получим эллипс, который будет являться натуральной величиной сечения цилиндра.
Разверткой цилиндра является прямоугольник с высотой, равной высоте цилиндра, и длиной, равной длине окружности основания 2πR. Для того, чтобы построить развертку усеченной части, основание цилиндра делят на равные части, тем самым аппроксимируя цилиндрическую поверхность призматической. Разделим окружность основания на 12 равных частей и отложим их вдоль горизонтальной линии развертки, по вертикали отложим высоту цилиндра (рис. 50).
Затем на полученных образующих отметим высоты точек сечения. Пристроим окружность основания и натуральную величину сечения.
Конус — это геометрическое тело, полученное путем ограничения конической поверхности плоскостью. Если в основании конуса лежит окружность, а высота попадает в центр основания, то конус называется прямым круговым.
На рисунке 51 построено сечение конуса фронтально — проецирующей плоскостью. Точки сечения находим при помощи вспомогательных секущих плоскостей. Точки С и D являются границей видимости для профильной проекции сечения.
Натуральную величину сечения находим способом вращения. Ось вращения выбираем в точке D и поворачиваем секущую плоскость до положения, параллельного горизонтальной плоскости проекций. Из горизонтальных проекций точек проводим линии, перпендикулярные оси вращения. Натуральной величиной сечения будет являться эллипс.
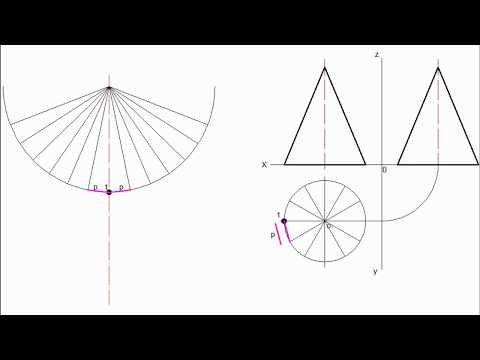
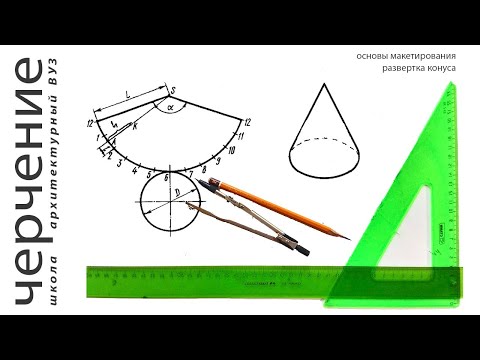
Развертка конуса является круговым сектором с радиусом, равным длине образующей конуса и длиной дуги, равной длине окружности основания конуса. Делим основание конуса на 12 равных частей и откладываем их по дуге на развертке. Затем на соответствующих образующих нужно отложить натуральные величины высот точек сечения. Чтобы получить полную развертку усеченной части, пристраиваем основание и натуральную величину сечения. На рисунке 52 показано построение развертки конуса.
1. Как образуется цилиндрическая поверхность?
2. Если секущая цилиндр плоскость фронтально проецирующая, то где будут лежать горизонтальные проекции точек сечения?
3. Какими способами можно определять натуральную величину фигуры сечения?
4. Какой геометрической фигурой является развертка боковой поверхности цилиндра? Конуса?
5. Для чего нужно разбивать окружность основания на некоторое количество равных частей?
6. Как построить развертку конической поверхности?
7. Как получить из полной развертки поверхности развертку ее усеченной части?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Видео:[Начертательная геометрия] Как сделать развертку цилиндра (построение в AutoCAD)Скачать
![[Начертательная геометрия] Как сделать развертку цилиндра (построение в AutoCAD)](https://i.ytimg.com/vi/XqmGLELwdX0/0.jpg)
Как сделать развертку цилиндра начертательная геометрия
Контрольные задания по теме:
Рабочая тетрадь задача 68, задача 69
Цилиндром будет называться геометрическое тело, полученное при ограничении цилиндрической поверхности двумя параллельными плоскостями — основаниями цилиндра. Если в основании цилиндра лежит окружность, а образующая перпендикулярна основанию, то цилиндр называется прямым круговым.
Линия сечения строится также при помощи опорных точек — точек пересечения секущей плоскости с очерковыми образующими и осью цилиндра. Но необходимо взять также промежуточные точки для более точного построения линии сечения. На рисунке 49 показано построение проекций сечения цилиндра фронтально — проецирующей плоскостью S. Так как цилиндр является проецирующей поверхностью, то горизонтальная проекция сечения совпадает с секущей плоскостью и на профильной проекции получим эллипс. Точки 2 и 3 будут являться границей видимости линии сечения для профильной плоскости.
Натуральную величину сечения можно определить способом вращения. Ось вращения выбираем в точке 1 и вращаем секущую плоскость до положения, параллельного горизонтальной плоскости. На горизонтальной плоскости получим эллипс, который будет являться натуральной величиной сечения цилиндра.
Разверткой цилиндра является прямоугольник с высотой, равной высоте цилиндра, и длиной, равной длине окружности основания 2πR. Для того, чтобы построить развертку усеченной части, основание цилиндра делят на равные части, тем самым аппроксимируя цилиндрическую поверхность призматической. Разделим окружность основания на 12 равных частей и отложим их вдоль горизонтальной линии развертки, по вертикали отложим высоту цилиндра (рис. 50).
Затем на полученных образующих отметим высоты точек сечения. Пристроим окружность основания и натуральную величину сечения.
Конус — это геометрическое тело, полученное путем ограничения конической поверхности плоскостью. Если в основании конуса лежит окружность, а высота попадает в центр основания, то конус называется прямым круговым.
На рисунке 51 построено сечение конуса фронтально — проецирующей плоскостью. Точки сечения находим при помощи вспомогательных секущих плоскостей. Точки С и D являются границей видимости для профильной проекции сечения.
Натуральную величину сечения находим способом вращения. Ось вращения выбираем в точке D и поворачиваем секущую плоскость до положения, параллельного горизонтальной плоскости проекций. Из горизонтальных проекций точек проводим линии, перпендикулярные оси вращения. Натуральной величиной сечения будет являться эллипс.
Развертка конуса является круговым сектором с радиусом, равным длине образующей конуса и длиной дуги, равной длине окружности основания конуса. Делим основание конуса на 12 равных частей и откладываем их по дуге на развертке. Затем на соответствующих образующих нужно отложить натуральные величины высот точек сечения. Чтобы получить полную развертку усеченной части, пристраиваем основание и натуральную величину сечения. На рисунке 52 показано построение развертки конуса.
1. Как образуется цилиндрическая поверхность?
2. Если секущая цилиндр плоскость фронтально проецирующая, то где будут лежать горизонтальные проекции точек сечения?
3. Какими способами можно определять натуральную величину фигуры сечения?
4. Какой геометрической фигурой является развертка боковой поверхности цилиндра? Конуса?
Читайте также: Пневматические цилиндры в нижнем новгороде
5. Для чего нужно разбивать окружность основания на некоторое количество равных частей?
6. Как построить развертку конической поверхности?
7. Как получить из полной развертки поверхности развертку ее усеченной части?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Видео:Развертка цилиндраСкачать

Развертка поверхности цилиндра в начертательной геометрии с примером
Развертка поверхности цилиндра:
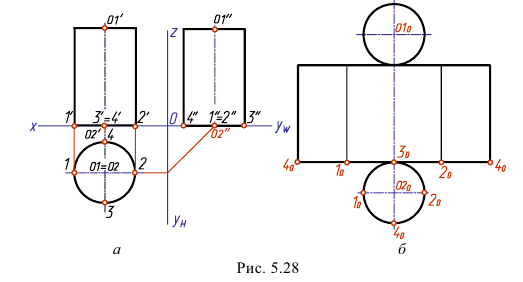
Развертка поверхности цилиндра представляет собой развернутую боковую поверхность цилиндра и его оснований, совмещенных в одной плоскости (рис. 5.28).
Для ее построения проводим прямую линию, на которой откладываем отрезок, равный длине окружности основания
Развертку боковой поверхности цилиндра можно выполнить приближенно, разделив окружность основания на 12 равных частей и отложив на прямой 12 хорд. Далее построение ведется, как описано выше.
- Инженерная графика
- Начертательная геометрия
- Компас
- Автокад
- Черчение
- Проекционное черчение
- Аксонометрическое черчение
- Строительное черчение
- Техническое черчение
- Геометрическое черчение
- Построение проекций линий пересечения конуса плоскостью
- Развертка поверхности конуса
- Шаровая поверхность
- Винтовые поверхности
- Развертка поверхности неправильной пирамиды
- Пирамида с вырезом
- Коническая и цилиндрическая поверхности
- Построение проекций линии пересечения цилиндра плоскостью
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать
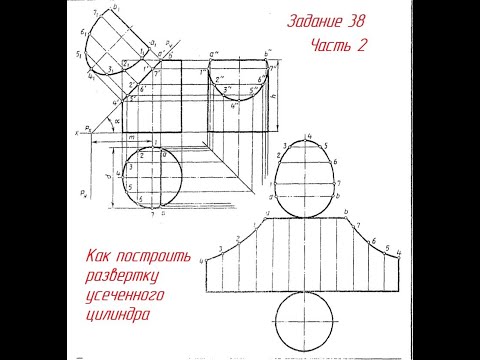
Развертка цилиндра
Цель задания — построение разверток поверхностей с нанесением линии пересечения поверхностей.
Дано: Чертеж «Взаимное пересечение поверхностей цилиндра и полусферы».
Необходимо: Построить развертку цилиндра и обозначить на ней линию взаимного пересечения поверхностей цилиндра и полусферы.
Мы уже чертили развертку цилиндра, поэтому повторим изученный материал. Тем более исходный чертеж и метод построения исходного чертежа отличается, от предыдущего.
Видео:Как начертить развёртку поверхностей цилиндра #чертёж #развёртка #цилиндрСкачать

Алгоритм построения развертки цилиндра
- Строим развертку боковой поверхности цилиндра.
- Делим основание цилиндра на 12 равных частей.
- Измеряем хорду между двумя любыми соседними точками деления окружности основания и откладываем это расстояние по нижней стороне развертки цилиндра.
Так как у нас только одна проекция (фронтальная) взаимного пересечения цилиндра и полусферы, то построим только профильную проекцию цилиндра. Профильную проекцию цилиндра со всеми вспомогательными построениями нужными для построения развертки цилиндра, выделим тонкими линиями и будет считать вспомогательными построениями.
Более подробно смотрите в видеоуроке.
Видео:Построение развертки цилиндра. Урок 37.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Видео «Развертка цилиндра»
Видео:[Начертательная геометрия] Как построить развертку конусаСкачать
ПОСТРОЕНИЕ РАЗВЕРТОК ПОВЕРХНОСТЕЙ Методические рекомендации по курсу начертательной геометрии
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Алтайский государственный технический университет им. И.И. Ползунова»
Видео:Развёртка цилиндраСкачать
Бийский технологический институт (филиал)
Г.И. Куничан, Л.И. Идт
Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать
ПОСТРОЕНИЕ РАЗВЕРТОК
Видео:Построение разверток пересекающихся цилиндра и конуса. Развертка конуса. Анимация.Скачать
ПОВЕРХНОСТЕЙ
Методические рекомендации по курсу начертательной геометрии
для самостоятельной работы студентов механических специальностей
171200, 120100, 171500, 170600
Куничан Г.И., Идт Л.И . Построение разверток поверхностей:
Методические рекомендации по курсу начертательной геометрии для самостоятельной работы студентов механических специальностей 171200, 120100, 171500, 170600.
Алт. гос. техн. ун-т, БТИ. – Бийск.
Изд-во Алт. гос. техн. ун-та, 2005. – 22с.
В методических рекомендациях подробно рассмотрены примеры построения разверток многогранников и поверхностей вращения по теме построение разверток поверхностей курса начертательной геометрии, которые изложены в виде лекционного материала. Методические рекомендации предлагаются для самостоятельной работы студентов дневной, вечерней и заочной форм обучения.
Протокол №20 от 05.02.2004 г.
Рецензент: завкафедрой МРСиИ БТИ АлтГТУ, к.т.н. Фирсов А.М.
Куничан Г.И., Идт Л.И., Леонова Г.Д., 2005
ОБЩИЕ ПОНЯТИЯ О РАЗВЕРТЫВАНИИ ПОВЕРХНОСТЕЙ
Представляя поверхность в виде гибкой, но нерастяжимой пленки, можно говорить о таком преобразовании поверхности, при котором поверхность совмещается
с плоскостью без складок и разрывов. Следует указать, что далеко не каждая поверхность допускает такое преобразование. Ниже будет показано, какие типы поверхностей возможно совместить с плоскостью при помощи изгибания, без растяжения и сжатия.Поверхности, которые допускают такое преобразование, называются развертывающимися , а фигура на плоскости, в которую поверхность преобразуется, называется разверткой поверхности .
Построение разверток поверхностей имеет большое практическое значение при конструировании различных изделий из листового материала. При этом необходимо отметить, что часто приходится изготовлять из листового материала не только развертывающиеся поверхности, но и неразвертывающиеся поверхности. В этом случае неразвертывающуюся поверхность разбивают на части, которые можно приближенно заменить развертывающимися поверхностями, а затем строят развертки этих частей.
К числу развертывающихся линейчатых поверхностей относятся цилиндрические, конические и торы.
Все остальные кривые поверхности не развертываются на плоскость и поэтому при необходимости изготовления этих поверхностей из листового материала их приближенно заменяют развертывающимися поверхностями.
1 ПОСТРОЕНИЕ РАЗВЕРТОК ПИРАМИДАЛЬНЫХ
Построение разверток пирамидальных поверхностей приводит к многократному построению натурального вида треугольников, из которых состоит данная пирамидальная поверхность или многогранная поверхность, вписанная (или описанная) в какую-либо коническую или линейчатую поверхность, которой заменяется указанная поверхность. Описываемый способ приводит к разбивке поверхности на треугольники, он называется способом треугольников (триангуляции).
Покажем применение этого способа для пирамидальных поверхностей. Если пренебречь графическими ошибками, то построенные развертки таких поверхностей можно считать точными.
Пример 1 . Построить полную развертку поверхности части треугольной пирамиды SABC .
Так как боковые грани пирамиды являются треугольниками, то для построения ее развертки нужно построить натуральные виды этих треугольников. Для этого предварительно должны быть определены натуральные величины боковых ребер. Натуральную величину боковых ребер можно определить при помощи прямоугольных треугольников, в каждом из которых одним катетом является превышение точки S над точками А , В и С , а вторым катетом – отрезок, равный горизонтальной проекции соответствующего бокового ребра (рисунок 1).
Так как стороны нижнего основания являются горизонталями, то их натуральные величины можно измерить на плоскости П 1 . После этого каждая боковая грань строится как треугольник по трем сторонам. Развертка боковой поверхности пирамиды получается в виде ряда примыкающих один к другому треугольников с общей вершиной S (S 2 C*, S 2 A*, S 2 B* – являются натуральными величинами ребер пира-миды).
Для нанесения на развертку точек D , E и F , соответствующих вершинам сечения пирамиды плоскостью, нужно предварительно определить их натуральные расстояния от вершины S , для чего следует перенести точки D* , E* и F* на соответствующие натуральные величины боковых ребер.
После построения развертки боковой поверхности усеченной части пирамиды, следует пристроить к ней треугольники АВС и DEF . Треугольник АВС является основанием усеченной пирамиды и изображен на горизонтальной плоскости проекций в натуральную величину.
2 ПОСТРОЕНИЕ РАЗВЕРТОК КОНИЧЕСКИХ
Рассмотрим построение разверток конических поверхностей. Несмотря на то, что конические поверхности являются развертывающимися и, следовательно, имеют теоретически точные развертки, практически строят их приближенные развертки, пользуясь способом треугольников . Для этого заменяют коническую поверхность вписанной в нее поверхностью пирамиды.
Читайте также: Процесс наполнения цилиндра четырехтактного дизеля
Пример 2 . Построить развертку прямого конуса с отсеченной вершиной (рису-нок 2а, б).
1. Необходимо предварительно построить развертку боковой поверхности конуса. Этой разверткой является круговой сектор, радиус которого равен натуральной величине образующей конуса, а длина дуги равна длине окружности основания конуса. Практически дугу сектора определяют при помощи ее хорд, которые принимают равными хордам, стягивающим дуги основания конуса. Иначе говоря, поверхность конуса заменяется поверхностью вписанной пирамиды.
2. Чтобы на развертку нанести точки фигуры сечения ( А,В,С,D,F,G,K ), нужно предварительно определить их натуральные расстояния от вершины S , для чего следует перенести точки А 2 , В 2 , С 2 , D 2 , F 2 , G 2 , K 2 на соответствующие натуральные величины образующих конуса. Так как в прямом конусе все образующие равны, то достаточно перенести проекции точек сечения на крайние образующие S 2 1 2 и S 2 7 2 . Таким образом, отрезки S 2 A*, S 2 B*, S 2 D*, S 2 F*, S 2 G*, S 2 K* являются искомыми, т.е. равными натуральной величине расстояния от S до точек сечения.
Пример 3. Построить развертку боковой поверхности эллиптического конуса с круговым основанием (рисунок 3).
В данном примере коническая поверхность заменяется поверхностью вписанной двенадцатиугольной пирамиды. Так как коническая поверхность имеет плоскость симметрии, то можно построить развертку только одной половины поверхности. Разделив от точки О половину окружности основания конической поверхности на шесть равных частей и определив с помощью прямоугольных треугольников натуральные величины образующих, проведенных в точки деления, строим шесть примыкающих один к другому треугольников с общей вершиной S.
Каждый из этих треугольников строится по трем сторонам; при этом две стороны равны натуральным величинам образующих, а третья – хорде, стягивающей дугу окружности основания между соседними точками деления (например О 1 -1 1 , 1 1 -2 1 , 2 1 — 3 1 и т.д.) После этого через точки 0, 1, 2 … разогнутого по способу хорд основания конической поверхности проводится плавная кривая.
Если на развертке надо нанести какую-либо точку М , находящуюся на поверхности конуса, то следует предварительно построить точку М* на гипотенузе S 2 –7* прямоугольного треугольника, с помощью которого определена натуральная величина образующей S – 7 , проходящей через точку М . После этого следует провести на развертке прямую S – 7 , определив точку 7 из условия равенства хорд 2 1 – 7 1 =2 – 7 , и на ней отложить расстояние SM=S 2 M* .
3 ПОСТРОЕНИЕ РАЗВЕРТОК ПРИЗМАТИЧЕСКИХ
И ЦИЛИНДРИЧЕСКИХ ПОВЕРХНОСТЕЙ
Построение разверток призматических и цилиндрических поверхностей приводит в общем случае к многократному построению натурального вида трапеций, из которых состоит данная призматическая поверхность, или призматическая поверхность, вписанная (или описанная) в цилиндрическую поверхность и заменяющая ее. Если, в частности, призматическая или цилиндрическая поверхности ограничены параллельными основаниями, то трапеции, на которые разбивается поверхность, обращаются в прямоугольники или параллелограммы, в зависимости от того, перпендикулярны или нет плоскости оснований боковым ребрам или образующим поверхности.
Построение трапеций или параллелограммов проще всего произвести по их основаниям и высотам, причем необходимо также знать отрезки оснований, на которые они делятся высотой. Поэтому для построения развертки призматической или цилиндрической поверхности необходимо предварительно определить натуральный вид нормального сечения данной поверхности. Стороны этого сечения, в случае призматической поверхности, и будут высотами трапеций или параллелограммов, из которых состоит поверхность. В случае цилиндрической поверхности высотами будут хорды, стягивающие дуги нормального сечения, на которые разделена кривая, ограничивающая это сечение.
Так как указанный способ требует построения нормального сечения, то он называется способом нормального сечения .
Покажем применение этого способа для призматических поверхностей. Если пренебречь графическими ошибками, то построенные развертки этих поверхностей можно считать точными.
Пример 4. Построить полную развертку поверхности треугольной призмы АВСDEF (рисунок 4).
Пусть данная призма расположена относительно плоскостей проекций так, что ее боковые ребра являются фронталями. Тогда они проецируются на плоскость проекций П 2 в натуральную величину и фронтально проецирующая плоскость S v , перпендикулярная боковым ребрам, определит нормальное сечение PQR призмы.
Построив натуральный вид P 4 Q 4 R 4 этого сечения, найдем натуральные величины P 4 Q 4 , Q 4 R 4 и R 4 P 4 — высот параллелограммов, из которых состоит боковая поверхность призмы.
Так как боковые ребра призмы параллельны между собой, а стороны нормального сечения им перпендикулярны, то из свойства сохранения углов на развертке следует, что на развертке призмы боковые ребра будут также параллельны между собой, а стороны нормального сечения развернутся в одну прямую. Поэтому для построения развертки призмы нужно отложить на произвольной прямой натуральные величины сторон нормального сечения, а затем через их концы провести прямые,
перпендикулярные к этой прямой. Если теперь отложить на этих перпендикулярах
по обе стороны от прямой QQ отрезки боковых ребер, измеренные на плоскости проекций П 2 , и соединить отрезками прямых концы отложенных отрезков, то получим развертку боковой поверхности призмы. Присоединяя к этой развертке оба основания призмы, получим ее полную развертку.
Если боковые ребра данной призмы имели бы произвольное расположение относительно плоскостей проекций, то нужно было бы предварительно преобразовать их в прямые уровня.
Существуют также другие способы построения разверток призматических поверхностей, один из которых – раскатка на плоскости – рассмотрим на примере 5.
Пример 5. Построить полную развертку поверхности треугольной призмы ABCDEF (рисунок 5).
Эта призма расположена относительно плоскостей проекций так, что ее ребра являются фронталями, т.е. на фронтальной плоскости проекций П 2 изображены в натуральную величину. Это позволяет использовать один из методов вращения, позволяющих находить натуральную величину фигуры путем вращения ее вокруг прямой уровня. В соответствии с этим методом точки B,C,A,D,E,F, вращаясь вокруг ребер AD, BE и CF, совмещаются с фронтальной плоскостью проекций. Т.е. траектория движения точек В 2 и F 2 изобразится перпендикулярно A 2 D 2 .
Раствором циркуля, равным натуральной величине отрезка АВ ( АВ=А 1 В 1 ), из точек А 2 и D 2 делаем засечки на траектории движения точек В 2 и F 2 . Полученная грань A 2 D 2 B F изображена в натуральную величину. Следующие две грани B F C E и C E AD строим аналогичным способом. Пристраиваем к развертке два основания АВС и DEF . Если призма расположена так, что ее ребра не являются прямыми уровня, то используя методы преобразования чертежа (замены плоскостей проекций или вращения), следует провести преобразование так, чтобы ребра призмы стали прямыми уровня.
Рассмотрим построение разверток цилиндрических поверхностей. Хотя цилиндрические поверхности являются развертывающимися, практически строят приближенные развертки, заменяя их вписанными призматическими поверхностями.
П ример 6. Построить развертку прямого цилиндра, усеченного плоскостью Sv (рисунок 6).
Построение развертки прямого цилиндра не представляет никакой сложности, т.к. является прямоугольником, длина одной стороны равняется 2πR, а длина другой равна образующей цилиндра. Но если требуется нанести на развертку контур усеченной части, то построение целесообразно вести, вписав в цилиндр двенад-цатигранную призму. Обозначим точки сечения (сечение является эллипсом), лежащие на соответствующих образующих, точками 1 2 , 2 2 , 3 2 … и по линиям связи
перенесем их на развертку цилиндра. Соединим эти точки плавной линией и пристроим натуральную величину сечения и основание к развертке.Читайте также: Перепускает главный тормозной цилиндр ваз 2112
Если цилиндрическая поверхность наклонная, то развертку можно строить двумя способами, рассмотренными ранее на рисунках 4 и 5.
П ример 7. Построить полную развертку наклонного цилиндра второго порядка (рисунок 7).
Образующие цилиндра параллельны плоскости проекций П 2, т.е. изображены на фронтальной плоскости проекций в натуральную величину. Основание цилиндра делят на 12 равных частей и через полученные точки проводят образующие. Развертку боковой поверхности цилиндра строят так же, как была построена развертка наклонной призмы, т.е. приближенным способом.
Для этого из точек 1 2 , 2 2 , …, 12 2 опускают перпендикуляры к очерковой образующей 1А и радиусом, равным хорде 1 1 2 1 , т.е. 1/12 части деления окружности основания, последовательно делают засечки на этих перпендикулярах. Например, делая засечку из точки 1 2 на перпендикуляре, проведенном из точки 2 2 , получают 2 . Принимая далее точку 2 за центр, тем же раствором циркуля делают засечку на перпендикуляре, проведенном из точки 3 2 , и получают точку 3 и т.д. Полученные точки 1 2 , 2 , 3 , … , 1 соединяют плавной лекальной кривой. Развертка верхнего основания симметрична развертке нижнего, так как сохраняется равенство длин всех образующих цилиндра.
4 ПРИБЛИЖЕННОЕ РАЗВЕРТЫВАНИЕ ШАРОВОЙ ПОВЕРХНОСТИ
Шаровая поверхность относится к так называемым неразвертываемым поверхностям, т. е. к таким, которые не могут быть совмещены с плоскостью, не претерпев при этом каких-либо повреждений (разрывов, складок). Таким образом, шаровая поверхность может быть развернута лишь приближенно.
Один из способов приближенной развертки шаровой поверхности рассмотрен на рисунке 8.
Сущность этого приема состоит в том, что шаровая поверхность при помощи меридианальных плоскостей, проходящих через ось шара SP , разбивается на ряд одинаковых частей.
На рисунке 8 шаровая поверхность разбита на 12 равных частей и показана горизонтальная проекция ( s 1 , k 1 , l 1 ) только одной такой части. Затем дуга k 4 l заменена прямой ( m 1 n 1 ) , касательной к окружности, и эта часть шаровой поверхности заменена цилиндрической поверхностью с осью, проходящей через центр шара и параллельной касательной тп. Далее дуга s 2 4 2 разделена на четыре равные части. Точки 1 2 , 2 2 , 3 2 , 4 2 приняты за фронтальные проекции отрезков образующих цилиндрической поверхности с осью, параллельной тп. Их горизонтальные проекции: a 1 b 1 , c 1 d 1 , e 1 f 1 , т 1 п 1 . Затем на произвольной прямой MN отложен отрезок тп . Через его середину проведен перпендикуляр к MN и на нем отложены отрезки 4 2 3 2 , 3 2 2 2 , 2 2 1 2 , 1 2 S 2 , равные соответствующим дугам 4 2 3 2 , 3 2 2 2 , 2 2 1 2 , 1 2 s 2 . Через полученные точки проведены линии, параллельные тп, и на них отложены соответственно отрезки а 1 b 1 , c 1 d 1 , e 1 f 1 . Крайние точки этих отрезков соединены плавной кривой. Получилась развертка 1 / 12 части шаровой поверхности. Очевидно, для построения полной развертки шара надо вычертить 12 таких разверток.
5 ПОСТРОЕНИЕ РАЗВЕРТКИ КОЛЬЦА
Пример 9 . Построить развертку поверхности кольца (рисунок 9).
Разобьем поверхность кольца при помощи меридианов на двенадцать равных частей и построим приближенную развертку одной части. Заменяем поверхность этой части описанной цилиндрической поверхностью, нормальным сечением которой будет средний меридиан рассматриваемой части кольца. Если теперь спрямить этот меридиан в отрезок прямой и через точки деления провести перпендикулярно к нему образующие цилиндрической поверхности, то, соединив их концы плавными кривыми, получим приближенную развертку 1/12 части поверхности кольца.
6 ПОСТРОЕНИЕ РАЗВЕРТКИ ВОЗДУХОВОДА
В заключение покажем построение развертки поверхности одной технической детали, изготовляемой из листового материала.
На рисунке 10 изображена поверхность, с помощью которой осуществляется переход с квадратного сечения на круглое. Эта поверхность состоит из двух
конических поверхностей I , двух конических поверхностей II , двух плоских треугольников III и плоских треугольников IV и V .Для построения развертки данной поверхности нужно предварительно определить натуральные величины тех образующих конических поверхностей I и II , с помощью которых эти поверхности заменяются совокупностью треугольников. На вспомогательном чертеже по способу прямоугольного треугольника построены натуральные величины этих образующих. После этого строят развертки конических поверхностей, а между ними в определенной последовательности строят треугольники III , IV и V , натуральный вид которых определяется по натуральной величине их сторон.
На чертеже (см. рисунок 10) показано построение развертки части от данной поверхности. Для построения полной развертки воздуховода следует достроить конические поверхности I, II и треугольник III.
На рисунке 11 приведен пример развертки воздуховода, поверхность которого можно разбить на 4 одинаковые цилиндрические поверхности и 4 одинаковые треугольника. Цилиндрические поверхности представляют собой наклонные цилиндры. Метод построения развертки наклонного цилиндра методом раскатки приведен подробно ранее на рисунке 7. Более удобным и наглядным для данной фигуры методом построения развертки представляется метод триангуляции, т.е. цилиндрическая поверхность разбивается на треугольники. А затем определяется натуральная величина сторон методом прямоугольного треугольника. Построение развертки цилиндрической части воздуховода обоими способами приведено на рисунке 11.
1. Укажите приемы построения разверток цилиндрических и конических поверхностей.
2. Как построить развертку боковой поверхности усеченного конуса, если нельзя достроить этот конус до полного?
3. Как построить условную развертку сферической поверхности?
4. Что называется разверткой поверхности?
5. Какие поверхности относятся к развертывающимся?
6. Перечислите свойства поверхности, которые сохраняются на ее развертке.
7. Назовите способы построения разверток и сформулируйте содержание каждого из них.
8. В каких случаях для построения развертки используются способы нормального сечения, раскатки, треугольников?
1. Гордон, В.О. Курс начертательной геометрии / В.О. Гордон, М.А. Семенцо-Огиевский; под ред. В.О. Гордона. – 25-е изд., стер. – М.: Высш. шк., 2003.
2. Гордон, В.О. Сборник задач по курсу начертательной геометрии / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева; под ред. В.О. Гордона. – 9-е изд., стер. – М.: Высш. шк., 2003.
3. Курс начертательной геометрии / под ред. В.О. Гордона. – 24-е изд, стер. – М.: Выcшая школа, 2002.
4. Начертательная геометрия / под ред. Н.Н. Крылова. – 7-е изд., перераб. и доп.- М.: Выcшая школа, 2000.
5. Начертательная геометрия. Инженерная и машинная графика: программа, контрольные задания и методические указания для студентов-заочников инже-нерно-технических и педагогических специальностей вузов / А.А. Чекмарев,
А.В. Верховский, А.А. Пузиков; под ред. А.А. Чекмарева. – 2-е изд., испр. – М.: Выcшая школа, 2001.6. Фролов, С.А. Начертательная геометрия / С.А. Фролов. – М.: Машиностроение, 1978.
7. Бубенников, А.В. Начертательная геометрия / А.В. Бубенников, М.Я. Громов. – М.: Высшая школа, 1973.
8. Начертательная геометрия / под общей ред. Ю.Б. Иванова. – Минск: Вышейшая школа, 1967.
9. Боголюбов, С.К. Черчение: учебник для машиностроительных специальностей средних специальных учебных заведений / С.К. Боголюбов. – 3-е изд., испр. и дополн. – М.: Машиностроение, 2000.
Общие понятия о развертывании поверхностей………………………………………. 3
1 Построение разверток пирамидальных поверхностей………………………………..3
2 Построение разверток конических поверхностей………………………………….….5
3 Построение разверток призматических и цилиндрических поверхностей………….9
4 Приближенное развертывание шаровой поверхности………………………….….. 14
5 Построение развертки кольца………………………………………………………. 14
6 Построение развертки воздуховода…………………………………………………. 16
🔍 Видео
36. Построение развертки цилиндра с линией пересеченияСкачать
16. Начертательная геометрия. РазверткиСкачать
Построение развертки конусаСкачать
Простой расчёт развёртки конусаСкачать
Развертка усеченного цилиндраСкачать
Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать
развертка конусаСкачать
Развертка усеченного цилиндра.Скачать
Развёртывание конусаСкачать


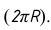
![[Начертательная геометрия] Как построить развертку конуса](https://i.ytimg.com/vi/ZIPjD9hsAUo/0.jpg)