- Круглый прямой цилиндр, развертка и формула для ее площади
- Цилиндр как фигура геометрии
- Круглый прямой цилиндр
- Развертка круглого прямого цилиндра
- Площадь развертки цилиндра
- Задача на нахождение радиуса фигуры
- Как сделать цилиндр из бумаги: пошаговая инструкция со схемой и видео
- Математическое значение
- История одной шляпы
- Мастерим шляпу фокусника
- Видео по теме статьи
- Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
- Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
- Развертка прямого кругового цилиндра.
- Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
- Развертка усеченного цилиндра.
- 💡 Видео
Видео:Видеоурок по математике "Цилиндр"Скачать

Круглый прямой цилиндр, развертка и формула для ее площади
Цилиндр — это одна из пространственных фигур, которая является объектом изучения стереометрии. Важная характеристика любой фигуры — это площадь ее поверхности. В данной статье рассмотрим, что собой представляет развертка цилиндра, а также покажем, как вычислить ее площадь.
Видео:Как сделать ИДЕАЛЬНЫЙ цилиндр из бумагиСкачать

Цилиндр как фигура геометрии
Предположим, что у нас имеется некоторая плавная кривая. Это может быть круг, эллипс, парабола и так далее. Возьмем отрезок произвольной длины, который не лежит в плоскости кривой, и опишем с помощью него поверхность, следуя направлению кривой и транслируя отрезок параллельно самому себе. Полученная поверхность называется цилиндрической или просто цилиндром. Отмеченная кривая называется директрисой (направляющей), а отрезок — генератрисой (образующей).
Если к цилиндрической поверхности добавить еще две плоские одинаковые фигуры, ограничивающие эту поверхность с торцов, то полученное тело также называется цилиндром. Оно состоит из двух равных оснований и цилиндрической поверхности.
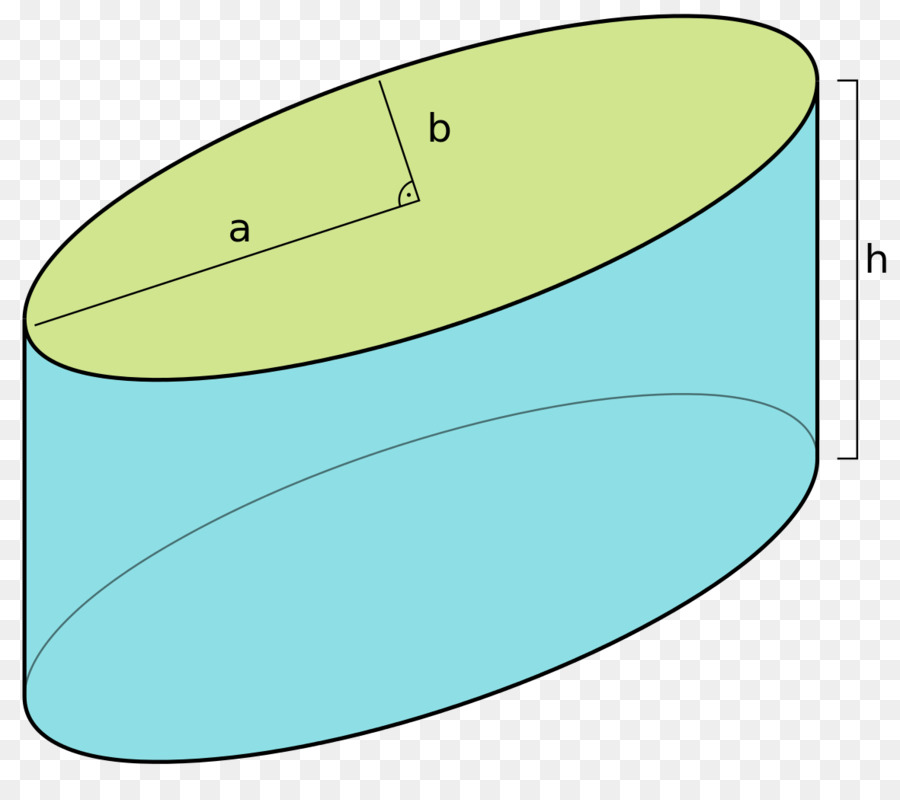
Для наглядного представления описанной фигуры ниже приведен рисунок. На нем изображен эллиптический цилиндр, имеющий полуоси a и b и высоту h (дистанция между основаниями).
Видео:Цилиндр - расчёт площади, объёма.Скачать

Круглый прямой цилиндр
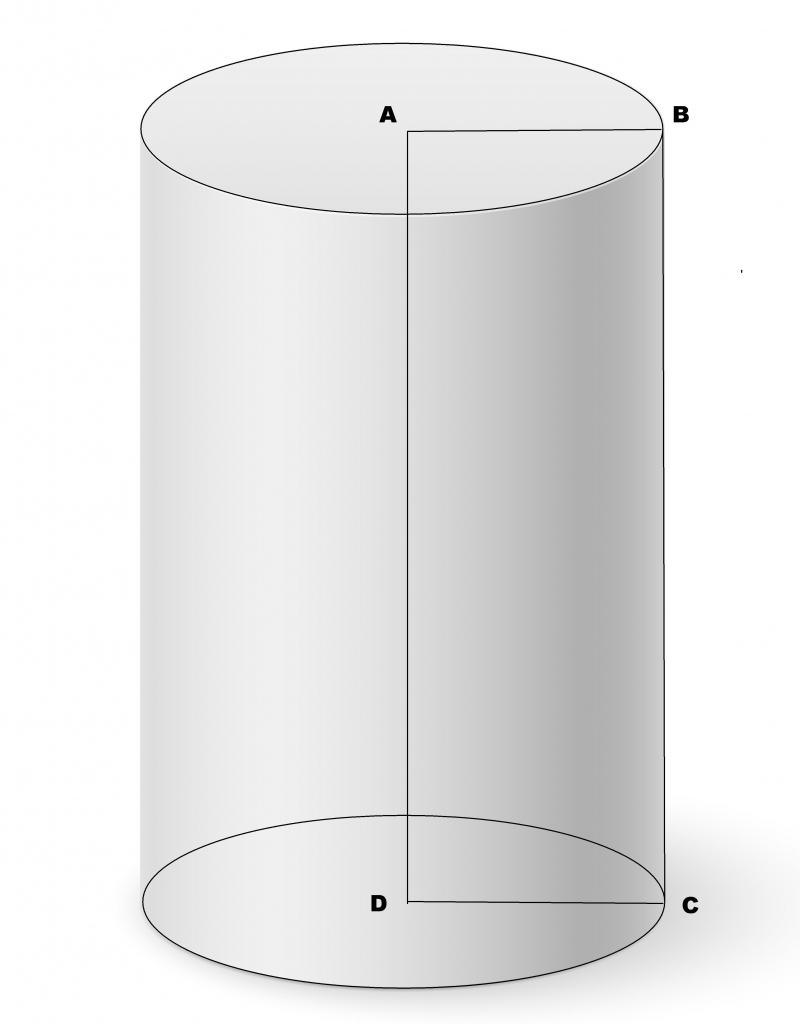
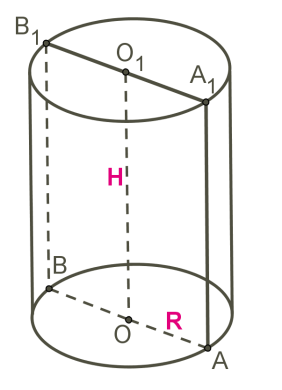
Пусть директрисой будет окружность некоторого радиуса. Тогда образованная генератрисой фигура будет называться круглым цилиндром. Тем не менее генератриса относительно плоскости, ограниченной директрисой, может быть направлена произвольным образом. Поэтому в общем случае говорят о наклонном круглом цилиндре. Если же генератриса будет перпендикулярна плоскостям основания, то цилиндр называется прямым. Он показан на рисунке ниже.
Здесь AB = DC — радиус цилиндра, AD = BC = h — высота фигуры. Для прямого цилиндра высота всегда равна длине образующей. Отрезок AD обозначает ось цилиндра — прямая, соединяющая две центральные точки оснований. От оси цилиндра все точки боковой поверхности лежат на одном расстоянии, равном радиусу фигуры.
Далее в статье будем рассматривать развертку поверхности цилиндра, круглого и прямого.
Видео:11 класс. Геометрия. Объем цилиндраСкачать

Развертка круглого прямого цилиндра
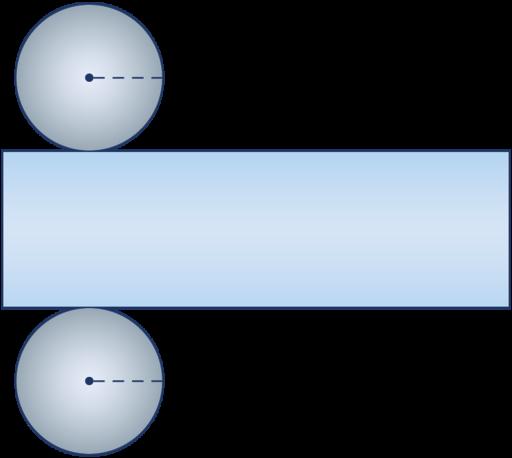
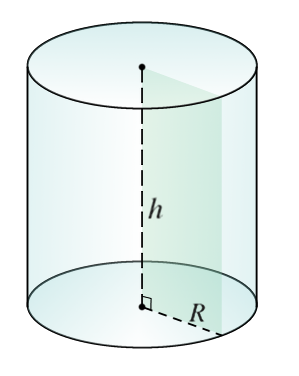
Когда говорят о развертке цилиндра, то подразумевают общую площадь его поверхности, представленную плоскими фигурами. Круглый прямой цилиндр образован двумя кругами, имеющими одинаковые радиусы, и одной боковой поверхностью, которая эти круги соединяет друг с другом.
На рисунке показан бумажный цилиндр. Как осуществляется построение развертки цилиндра? Возьмем воображаемые ножницы и отрежем одно основание вдоль окружности. Затем проделаем аналогичные действия со вторым основанием. Боковую поверхность разрежем вдоль генератрисы, то есть параллельно оси фигуры, и развернем ее. Таким образом, мы получили развертку, которая показана на рисунке ниже.
Очевидно, что она состоит из двух одинаковых кругов. Что касается цилиндрической поверхности, то в разрезанном виде она представлена прямоугольником. Развертку удобно использовать при определении площади поверхности рассматриваемой фигуры.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Площадь развертки цилиндра
Выше мы показали, как можно получить развертку фигуры. Чтобы рассчитать ее площадь, необходимо сложить площади для всех ее частей, то есть для двух круглых оснований и одного прямоугольника.
Читайте также: Как построить пересечение цилиндра с прямой
Обозначим радиус основания буквой r, а высоту фигуры — буквой h. Площадь одного основания равна площади круга, то есть:
Здесь pi — число Пи, приблизительно равное 3,14.
Чтобы вычислить площадь прямоугольника, представляющего боковую поверхность фигуры в развернутом виде, необходимо знать две его стороны. Одна из них равна высоте h. Вторая, как можно догадаться, соответствует длине директрисы, то есть длине окружности. Обозначим ее l. Тогда можно записать следующие равенства:
Здесь Sb — площадь прямоугольника, равная площади цилиндрической поверхности.
Учитывая, что фигура имеет два основания, складываем рассчитанные величины, получаем общую площадь развертки цилиндра:
Площадь S фигуры однозначно определяется через ее радиус и высоту.
Покажем, как использовать это равенство для решения геометрической задачи.
Видео:Простой расчёт развёртки конусаСкачать

Задача на нахождение радиуса фигуры
Известно, что общая поверхность круглого прямого цилиндра составляет 60 см 2 . Чему равен радиус основания цилиндра, если его высота равна 7 см, а фигура имеет лишь одно основание.
Описанный в условии задачи цилиндр представляет собой бочку без крышки, поэтому площадь его поверхности образована не двумя, а одним основанием.
Если учесть названный факт, тогда формула для площади фигуры запишется в следующем виде:
Подставим все известные из условия величины в это равенство, получим:
Мы получили классическое полное квадратное уравнение. Его решение даст искомое значение радиуса r. Решаем через дискриминант:
При решении уравнения отрицательный корень был отброшен, в виду его нефизического значения.
Таким образом, параметры открытого цилиндра из условия задачи составляют 7 см в высоту и 2,5 см в диаметре.
Видео:Как выполнить модель цилиндра #модель #цилиндрСкачать

Как сделать цилиндр из бумаги: пошаговая инструкция со схемой и видео
У слова цилиндр два значения. С точки зрения математики — это геометрическое тело, а с точки зрения моды — это шляпа. Пошаговая инструкция, как сделать цилиндр из бумаги своими руками, поможет и вам сделать такую шляпку.
Видео:Как сделать цилиндр из бумаги.Скачать

Математическое значение
Цилиндр является геометрическим телом, в котором цилиндрическая поверхность ограничена двумя пересекающими ее плоскостями. Он имеет боковую поверхность и два основания.
Попробуем сделать такую геометрическую фигуру из бумаги. Сначала попрактикуйтесь делать цилиндр без точных замеров. Для его изготовления вам понадобится:
Возьмите лист бумаги формата А4 и подогните с длинных сторон на 2-2,5 см.
С одной из сторон отмерьте снизу и сверху по 22 мм и вырежьте. Это будет припуск для склейки бокового шва.
Теперь длинные края нужно нарезать ножницами на полоски по 5-7 мм.
Начертите циркулем 2 круга диаметром 90 мм и приклейте их к нарезанным боковым сторонам, предварительно смазав их клеем.
Такие схемы называются развертками. По сути, они изображают разобранную геометрическую фигуру с точными расчетами ее параметров. Высота цилиндра обозначена буквой h. Для расчета длинной стороны цилиндра L воспользуйтесь формулой L=π*d, где d это диаметр основания цилиндра.
При работе нужно сделать припуски для склеивания размером 5-7 мм.
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

История одной шляпы
Ну вот, с геометрической фигурой разобрались, теперь поговорим о моде. В конце XVIII начале XIX веков европейскими шляпными мастерами была изобретена необычная шляпа – цилиндр.
Представлял он собой высокую (до 30 см) шляпу с плоским верхом и полями. Из-за дороговизны материала, из которого делали эти шляпы, ношение цилиндра считалось привилегией высших слоев общества. Изначально для изготовления шляп брали бобровый фетр, чем и поставили бедных зверушек на грань вымирания. Чуть позже в моду вошли шикарные шелковые цилиндры.
Читайте также: Плоскость a пересекает плоскости основания цилиндра по хордам
Простолюдины тоже носили шляпы, похожие на цилиндр, только делали их из фетра и войлока. При обработке этих материалов использовались соли ртути, очень вредные для здоровья. История Льюиса Кэролла о безумном шляпнике берет свои корни именно отсюда – пары ртути вызывали слабоумие у мастеров шляпного дела. Пожалуй, самым знаменитым человеком, одевавшим такую шляпу на голову, являлся Авраам Линкольн. И пользовался он цилиндром не только как предметом своего гардероба. Он также являлся хранилищем для секретной корреспонденции. По достоинству оценили этот головной убор и фокусники. Большой размер тульи позволял сделать двойное дно и спокойно достать кролика из такой шляпы. Сейчас цилиндр выполняет декоративную функцию, его часто можно встретить на стилистических вечеринках и свадьбах, на магических шоу.
Видео:Цилиндр, конус, шар, 6 классСкачать

Мастерим шляпу фокусника
Задумали сделать карнавальный костюм фокусника? Тогда эта пошаговая инструкция поможет вам сделать его главный атрибут – цилиндр.
Научившись делать цилиндр из бумаги, можно с легкостью сотворить карнавальную шляпку. Для ее изготовления вам понадобится:
- Картон черного цвета;
- Ножницы;
- Карандаш;
- Скотч;
- Клей;
- Полоса черного флиса;
- Лак и кисть;
Первым делом нужно снять мерки. Измерьте окружность головы с помощью сантиметровой ленты. Подумайте, какой высоты будет ваша шляпа и какого размера будут ее поля. Делая бумажный цилиндр, сделайте донышко и тулью шляпы, склейте детали. Для изготовления полей шляпы нужно полученный цилиндр без донышка приложить к картону и обвести. Следующий круг нужно начертить из той же середины, его размер относительно первого круга и будет размером полей вашей шляпы. Чтобы было понятнее, взгляните на картинку:
Далее нужно сделать вторую деталь полей, которая будет крепиться к тулье шляпы. Ее размер такой же, как у первой детали, но не торопитесь вырезать. Внутри этой детали нужно начертить круг, диаметр которого будет на 1 см меньше диаметра основания цилиндра. Вырежьте деталь и нарежьте бахромой внутренний круг.
Склейте две детали полей между собой.
Осталось только смазать зубцы клеем и приделать поля к шляпе. Внутри тульи приклейте полоску из флиса, равную окружности головы. Она нужна, чтобы шляпа плотно сидела на голове. Покройте готовую шляпу лаком и украсьте лентой. Можно отправляться на карнавал!
Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Видео по теме статьи
Небольшая подборка видео поможет вам освоить все нюансы в изготовлении шляпы из бумаги.
Видео:КАК СДЕЛАТЬ ЦИЛИНДР ИЗ БУМАГИ? КАК СДЕЛАТЬ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ? ГЕОМЕТРИЧЕСКИЕ ТЕЛА. | #RAIDOTVСкачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Видео:Объем цилиндраСкачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
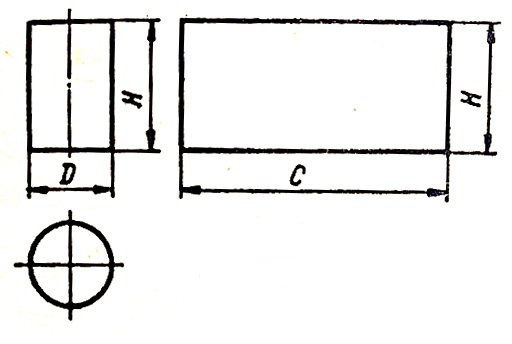
Развертка прямого кругового цилиндра.
Цилиндр диаметром D и высотой H показан на рис. 1. Развертка представляет собой прямоугольник длиной с = πD и высотой Н.
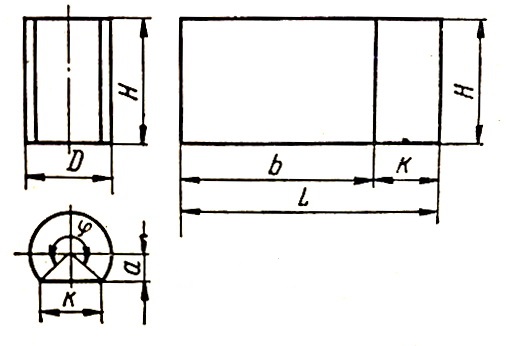
Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2) 2 – a 2 ) = 2a tg (ᵠ/2).
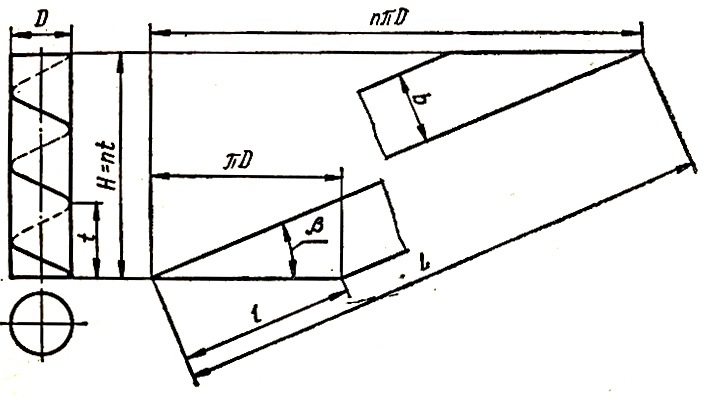
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
Цилиндр показан на рис. 3. При определении развертки можно использовать следующие зависимости:
n — число полных витков на общей длине цилиндра H, Н = nt;
Развертка усеченного цилиндра.
Для получения развертки горизонтальная проекция цилиндра делится на равные части и точки деления нумеруются (в данном случае от 0 до 12). Из точек деления проводятся вертикали до пересечения верхнего основания в точках 0′1, 1′1…, 6′1. На продолжении прямой 0’6′ откладывается отрезок длиной с = πD, который делится на принятое число равных частей. Из точек деления 00, 10, …, 60 строятся перпендикуляры до их пересечения с соответствующими горизонтальными линиями в точках 0 0 1, 1 0 1, …, 6 0 1. Полученные точки соединяются плавной кривой. Ввиду симметричности остальные точки кривой находит аналогичным путем.
Читайте также: Двигатель ламборджини дизель 2 цилиндра 9ld625 2
Линию развертки можно определить и таким способом. На расстоянии h1 = (h + H)/2 от линии 0 0 12 0 проводится параллельная прямая. Из центра S, лежащего на прямой, описывается полуокружность радиусом А. Полуокружность делится на равные части, число которых равно половине точек деления развертки (в данном случае на шесть). Через точки деления 0ꞋꞋ, 1ꞋꞋ, …, 6ꞋꞋ проводятся горизонтальные прямые до пересечения вертикалей, проходящих через 0 0 , 1 0 , … , 12 0 . Полученные точки 0 0 1, 1 0 1, …, 12 0 1 соединяются плавной кривой.
Верхнее основание цилиндра представляет собой эллипс с полуосями a = D/2 cos α = 0′13′1 и b = D/2.
При аналитическом определении координат точек кривой развертки цилиндра, усеченного плоскостью под углом α (рис. 5), могут быть использованы следующие зависимости:
xk = kx1 = πD/2 kε/180°; yk = D/2 tg α sin kε = A sin kε = A sin ᵠi,
где х1 = πD/ (2n) = πD/2 ε/180° — длина дуги окружности основания цилиндра, разделенная на 2n равных частей; ε = 360°/2n — центральный угол, соответствующий одному делению; k — порядковый номер точки; A = (H — h)/2 = (D/2) tg α — амплитуда синусоиды; ᵠi= kε.
Значения sin kε для наиболее часто употребляемых значений 2n приведены в табл. 1.
Таблица 1. Значения sin kε и sin 2 kε
| 2n | sin kε | sin 2 kε | 2n | sin kε | sin 2 kε | ||||||
| 8 | 16 | 32 | 64 | 12 | 24 | 48 | 96 | ||||
| — | — | — | 1 | 0,09802 | 0,00961 | — | — | — | 1 | 0,06540 | 0,00428 |
| — | — | 1 | 2 | 0,19509 | 0,03806 | — | — | 1 | 2 | 0,13053 | 0,01704 |
| — | — | — | 3 | 0,29028 | 0,08426 | — | — | — | 3 | 0,19509 | 0,03806 |
| — | 1 | 2 | 4 | 0,38268 | 0,14645 | — | 1 | 2 | 4 | 0,25882 | 0,06699 |
| — | — | — | 5 | 0,47139 | 0,22221 | — | — | — | 5 | 0,32144 | 0,10332 |
| — | — | 3 | 6 | 0,55557 | 0,30866 | — | — | 3 | 6 | 0,38268 | 0,14645 |
| — | — | — | 7 | 0,63439 | 0,40245 | — | — | — | 7 | 0,44229 | 0,19562 |
| 1 | 2 | 4 | 8 | 0,70711 | 0,50000 | 1 | 2 | 4 | 8 | 0,50000 | 0,25000 |
| — | — | — | 9 | 0,77301 | 0,59754 | — | — | — | 9 | 0,55557 | 0,30866 |
| — | — | 5 | 10 | 0,83147 | 0,69134 | — | — | 5 | 10 | 0,60876 | 0,37059 |
| — | — | — | 11 | 0,88192 | 0,77778 | — | — | — | 11 | 0,65935 | 0,43474 |
| — | 3 | 6 | 12 | 0,92388 | 0,85355 | — | 3 | 6 | 12 | 0,70711 | 0,50000 |
| — | — | — | 13 | 0,95694 | 0,91573 | — | — | — | 13 | 0,75184 | 0,56526 |
| — | — | 7 | 14 | 0,98079 | 0,96194 | — | — | 7 | 14 | 0,79335 | 0,62941 |
| — | — | — | 15 | 0,99518 | 0,99039 | — | — | — | 15 | 0,83147 | 0,69134 |
| 2 | 4 | 8 | 16 | 1,00000 | 1,00000 | 2 | 4 | 8 | 16 | 0,86617 | 0,75000 |
| — | — | — | 17 | 0,89687 | 0,80438 | ||||||
| — | — | 9 | 18 | 0,92388 | 0,85355 | ||||||
| — | — | — | 19 | 0,94693 | 0,89668 | ||||||
| — | 5 | 10 | 20 | 0,96600 | 0,93301 | ||||||
| — | — | — | 21 | 0,98079 | 0,96194 | ||||||
| — | — | 11 | 22 | 0,99144 | 0,98296 | ||||||
| — | — | — | 23 | 0,99786 | 0,99572 | ||||||
| 3 | 6 | 12 | 24 | 1,00000 | 1,00000 | ||||||
Примечание: Значения sin kε и sin 2 kε даны для одной четверти окружности. В остальных четвертях они повторяются.
Ввиду симметричности синусоиды достаточно определить координаты точек одной четверти окружности, например от у0 до у3. Остальные координаты имеют соответственно равные значения. Например: у4 — у2, …, у11 = — у1 и т. д.
💡 Видео
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

КАК СДЕЛАТЬ ЦИЛИНДР ИЗ БУМАГИ СВОИМИ РУКАМИ ЛУЧШИЙ СПОСОБСкачать

Усеченный конус. 11 класс.Скачать

Уроки Компас 3D.Развертка цилиндраСкачать

Физичка:Вечного двигателя не существует! Даник на последней парте!Скачать