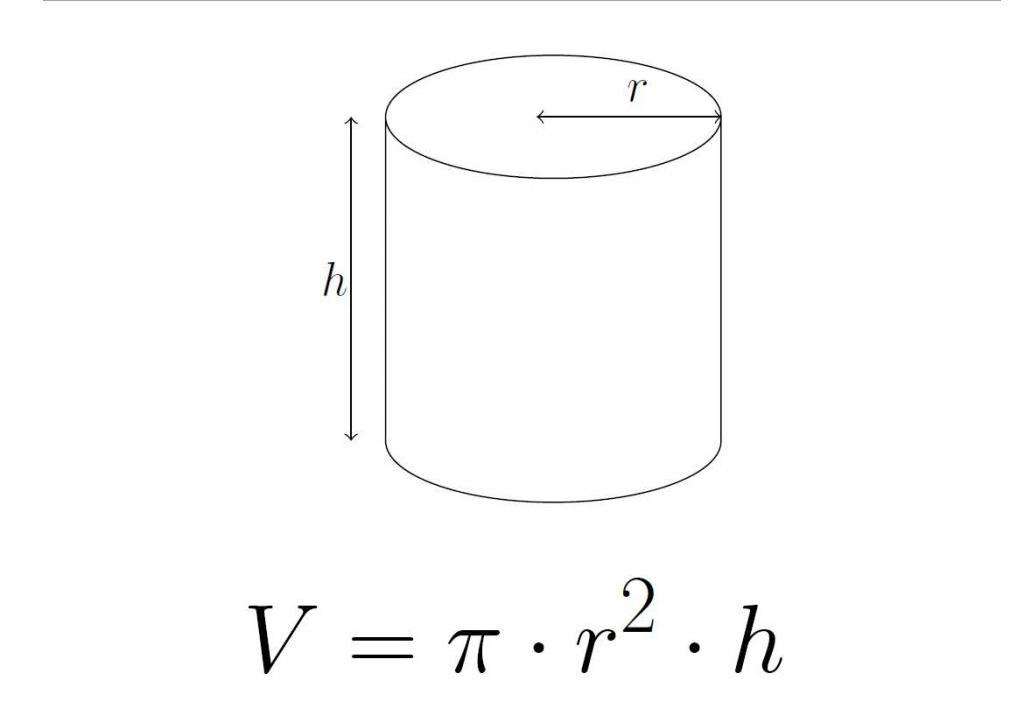Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
- Объем правильного цилиндра через радиус и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
- Объем цилиндрической полости
- Поверхности цилиндра
- Сечения цилиндра
- Что такое объем
- Формула объема цилиндра: пример решения задачи
- Объем тел
- Понятие о цилиндре
- Формула объема цилиндра
- Вычисление объема бочки
- Формулы, позволяющие находить объём цилиндра в метрах и литрах
- Типы цилиндров
- Вычисление объёма
- Исходные данные
- Методы расчёта
- Объём в литрах
- Видео
- Видео
Видео:Объём цилиндраСкачать

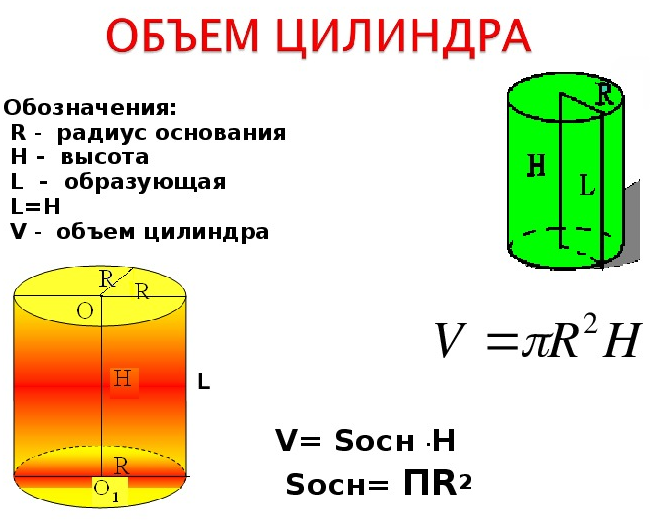
Объем правильного цилиндра через радиус и высоту цилиндра
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
Видео:Отношение объёмов цилиндровСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
Видео:Объем цилиндра.Скачать

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Видео:Видеоурок по математике "Цилиндр"Скачать

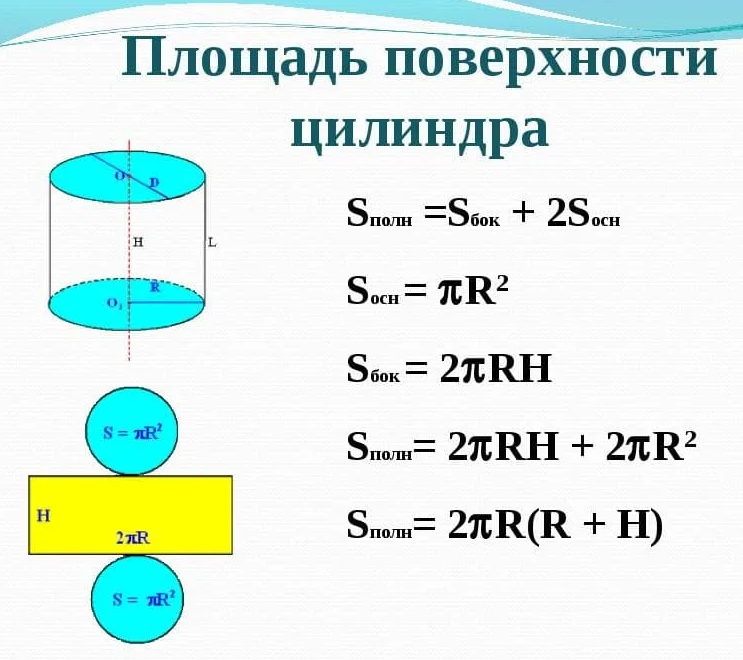
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Видео:11 класс. Геометрия. Объем цилиндраСкачать

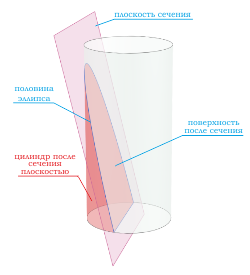
Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
Читайте также: Ваз 2114 как порядок цилиндров
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .
Видео:Объем цилиндраСкачать

Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Видео:Объем цилиндра. Урок 13. Геометрия 11 классСкачать

Формула объема цилиндра: пример решения задачи
Объем является физической величиной, которая присуща телу с ненулевыми размерами вдоль каждого из трех направлений пространства (все реальные объекты). В статье в качестве примера формулы объема рассматривается соответствующее выражение для цилиндра.
Видео:11 класс, 32 урок, Объем цилиндраСкачать

Объем тел
Эта физическая величина показывает, какую часть пространства занимает то или иное тело. Например, объем Солнца намного больше этой величины для нашей планеты. Это означает, что принадлежащее Солнцу пространство, в котором находится вещество этой звезды (плазма), превышает земную пространственную область.
Объем изменяется в кубических единицах длины, в СИ это метры в кубе (м3). На практике объемы жидких тел измеряют в литрах. Маленькие объемы могут выражать в кубических сантиметрах, миллилитрах и других единицах.
Для вычисления объема формула будет зависеть от геометрических особенностей рассматриваемого объекта. Например, для куба это тройное произведение длины его ребер. Ниже рассмотрим фигуру цилиндр и ответим на вопрос о том, как найти объем его.
Видео:Геометрия 11 класс (Урок№12 - Объемы прямой призмы и цилиндра.)Скачать

Понятие о цилиндре
Фигура, о которой пойдет речь, является достаточно непростой. Согласно геометрическому определению, она представляет собой поверхность, образованную путем параллельного перемещения прямой (генератрисы) вдоль некоторой кривой (директрисы). Генератриса также называется образующей, а директриса — направляющей.
Если директриса — это окружность, а генератриса перпендикулярна ей, тогда полученный цилиндр называют круглым и прямым. О нем и пойдет дальше речь.
Цилиндр имеет два основания, которые параллельны друг другу и соединены цилиндрической поверхностью. Проходящая через центры двух оснований прямая называется осью круглого цилиндра. Все точки фигуры находятся на одинаковом расстоянии от этой прямой, которое равно радиусу основания.
Круглый прямой цилиндр однозначно определяется двумя параметрами: радиусом основания (R) и расстоянием между основаниями — высота H.
Видео:Поршни одинаковые, а объемы разные на мопеде Альфа.Скачать

Формула объема цилиндра
Для расчета области пространства, которую занимает цилиндр, достаточно знать его высоту H и радиус основания R. Искомое равенство в этом случае имеет вид:
Понять эту формулу объема просто: поскольку высота перпендикулярна основаниям, то если ее умножить на площадь одного из них, получается нужная величина V.
Читайте также: Деталь состоит из двух соосных цилиндров
Видео:Съемник Дизельных Форсунок KHAMM. Сравнение с другими съемниками, нужно ли переплачивать.Скачать

Вычисление объема бочки
Для примера решим такую задачу: определим, сколько воды поместится в бочку, имеющую диаметр дна 50 см и высоту 1 метр.
Радиус бочки равен R=D/2=50/2=25 см. Подставляем данные в формулу, получаем:
V = pi*R2*H = 3,1416*252*100 = 196350 см3
Поскольку 1 л = 1 дм3 = 1000 см3, то получаем:
V = 196350/1000 = 196,35 литра.
То есть в бочку можно налить почти 200 литров воды.
Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Формулы, позволяющие находить объём цилиндра в метрах и литрах
Среди множества геометрических фигур часто встречается и цилиндр. Это геометрическое тело применяется в многочисленных расчётах. Согласно принятой терминологии под таким понятием принято иметь ввиду тело геометрического типа, которое в своей основе имеет поверхность. Данная поверхность представляет также цилиндрическую форму.
В литературе данная поверхность часто именуется, как поверхность бокового вида. Кроме этого, в такой фигуре есть пара поверхностей, носящих наименование оснований. Эти основания цилиндра представляют собой окружности равного диаметра. Цилиндр, в основании которого находится круг принято считать круговым.
Ещё со школьных времён знакома всем фигура цилиндра классического типа. Это и есть круговой цилиндр.
Видео:Зачем нужен БОЛЬШОЙ обьем двигателя?Скачать

Типы цилиндров
В математике существует несколько типов цилиндров, которые постоянно используются в геометрии.
- Цилиндр прямого типа. Это геометрическая фигура, которая имеет прямой угол между боковой поверхностью и основаниями. Такой тип самый распространённый и часто применяется в решении большого количества задач.
- Наклонный цилиндр. Исходя из основания фигуры, можно сделать вывод, что угол между боковой поверхностью и основаниями фигуры будет отличным от прямого. При этом он может колебаться в своём значении, как в большую, так и в меньшую сторону от прямого угла.
Видео:КАК ИЗМЕРИТЬ ЦИЛИНДРЫ? Учимся пользоваться нутромером и микрометромСкачать

Вычисление объёма
Довольно часто для работы с цилиндрами требуется вычислить его объём. Это процедура в последнее время производится с применением вычислительной техники. Однако, чтобы провести такую процедуру необязательно использовать калькулятор и другие дополнительные методы решения поставленной задачи.
Сейчас существует несколько основных методов, которые позволяют произвести вычисление данного параметра. Это, по сути, универсальные формулы. Каждая из таких формул имеет свои входные параметры, отталкиваясь от которых и можно найти требуемое значение объёма. Это позволяет достигнуть ряда положительных моментов в расчётах.
- Значительно сокращается время для осуществления операций подсчёта объёма.
- Уменьшается вероятность того что может быть совершена ошибка в расчётах
- Требуется для вычисления ограниченное число параметров, знание которых и даёт возможность достигать результата.
Видео:(0.02 мм) ДВЕ СОТКИ которые СПАСУТ твой двигательСкачать

Исходные данные
Производя вычисление такого параметра, как объём, необходимо помнить, что требуется первоначальное знание параметра, который и будет исходным данным для такой процедуры.
Необходимо иметь значение высоты. Это расстояние от нижнего и верхнего основания фигуры. При этом в зависимости от типа она может определяться по-разному. В ситуации прямоугольного цилиндра высота соответствует расстоянию между основаниями фигуры. Если же он относится к наклонному типу, то расстояние будет вычисляться иным путём. Это параметр, который соответствует длине прямой проведённой под прямым углом от одного основания до плоскости, на которой лежит второе основание.
После определения такого значения можно приступать к вычислению объёма.
Видео:Сравниваем цилиндр мопеда Альфа 110 и 125 куб. см.Скачать

Методы расчёта
Существует два основных метода, которые позволяют производить вычисление такого параметра.
- Метод вычисления объёма цилиндра на основе высоты геометрической фигуры. Этот метод является универсальным средством и может быть использован для фигур любого типа как прямоугольных, так и наклонных цилиндров. Дополнительно к значению высоты в данном способе следует знать и площадь основания. Если остановиться подробнее на данном параметре, то надо отметить что основанием является круг. Поэтому вычисление площади круга происходит на основе радиуса. Таким образом, вторым параметром в данном методе должен выступать радиус основания цилиндра. Тогда площадь определяется согласно стандартной формуле.
Читайте также: Соединение главного тормозного цилиндр
В данной формуле принято следующее обозначение при помощи переменных:
- П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
- R – Радиус окружности, лежащий в основании цилиндра.
- S — Площадь основания фигуры.
Вычисление непосредственно объёма цилиндра производится на основе стандартной формулы.
В данной формуле принято следующее обозначение при помощи переменных:
- S – Площадь основания цилиндра, имеющего форму круга.
- h – Высота геометрической фигуры.
- V – объём цилиндра.
- Вторым методом, позволяющим произвести вычисление объёма данной фигуры, является соотношение таких параметров, как высота цилиндра и радиуса его основания. По сути, данная формула является преобразованной формулой первого метода. В ней нет разделения на промежуточные этапы подсчёта параметров. Сразу же включены все математические операции.
Таким образом, в ней одновременно производится подсчёт площади круга и объёма цилиндра.
Приведём формулу расчёта объёма цилиндра для данного метода.
В данной формуле принято следующее обозначение при помощи переменных:
- П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
- R – Радиус окружности, лежащий в основании цилиндра.
- h – Высота геометрической фигуры.
- V – Объём цилиндра.
Видео:как замерить выработку поршня и цилиндраСкачать

Объём в литрах
Если говорить о нахождении объёма такой геометрической фигуры, то надо отметить что это задача не только для школьной программы. Используя приведенные ранее методы, есть возможность производить расчёты объёма ёмкости неизвестного типа.
К примеру, есть возможность вычислить объём ёмкости для полива на садовом участке. Однако есть и особенность при проведении подсчёта. Надо все значения подставлять в формулы в метрах. В результате проведения расчётом получается значение, которое будет измеряться в кубических метрах.
Однако, принято при расчётах поливных ёмкостей пользоваться измерениями в литрах. Для этого необходимо произвести пересчёт полученного значения объёма в литры. Это происходит на основе простого соотношения, где один кубический метр равняется 1000 литрам жидкости.
Если вычисления происходят в сантиметрах, то и результат будет в кубических сантиметрах. Тогда надо понимать, что между кубическими сантиметрами и литрами существует чёткое соотношение. Перевод происходит путём деления полученного значения объёма на 1000. После этого данные будут представлены в литрах.
Если необходимо первоначально перевести полученный в результате вычислений параметр из кубических сантиметров в кубические метры, то достаточно произвести операцию деления. Объём делится на 1000000. Это связано с тем, что кубический метр — это куб, у которого сторона равняется 100 сантиметрам. Поэтому объём в сантиметрах будет равен произведению 100*1000*100. Соответственно это будет 1000000 сантиметров кубических.
Видео:Отличие цилиндров 110-125сс на мопед alpha, vento и т.п.Скачать

Видео
Посмотрите, как высчитать объем цилиндра и площадь его поверхности.
🎬 Видео
Про объемы двигателей бензопил и бензокосСкачать