Как строить аксонометрию цилиндра (2 видео)

Построение аксонометрических проекций начинают с проведения аксонометрических осей.

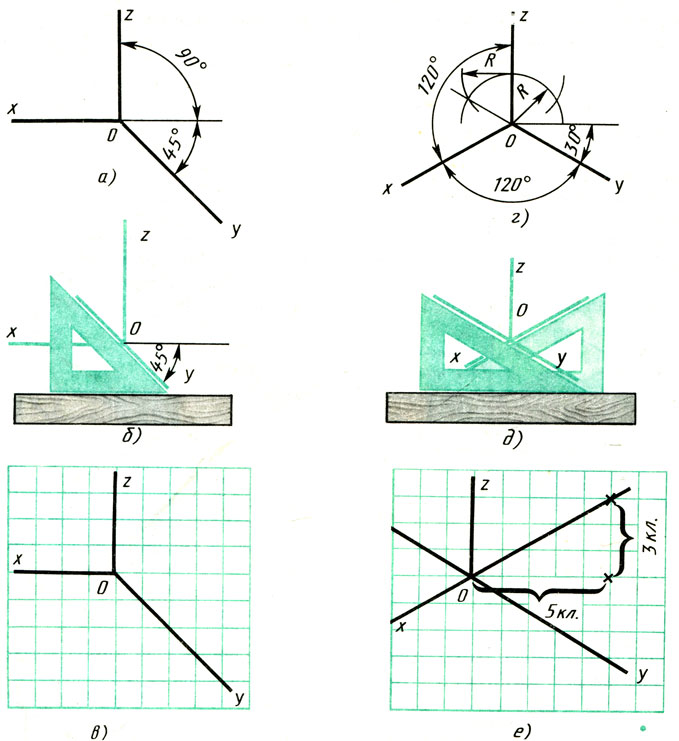
Положение осей. Оси фронтальной ди-метрической проекции располагают, как показано на рис. 85, а: ось х — горизонтально, ось z — вертикально, ось у — под углом 45° к горизонтальной линии.

Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 85, б.

Положение осей изометрической проекции показано на рис. 85, г. Оси х и у располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис. 85, д).

Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О.

При построении фронтальной диметрической проекции по осям х и z (и параллельно им) откладывают действительные размеры; по оси у (и параллельно ей) размеры сокращают в 2 раза, отсюда и название «диметрия», что по-гречески означает «двойное измерение».

При построении изометрической проекции по осям х, у, z и параллельно им откладывают действительные размеры предмета, отсюда и название «изометрия», что по-гречески означает «равные измерения».

На рис. 85, в и е показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 85, в). Наклон оси в 30° (рис. 85, г) получается при соотношении длин отрезков 3 : 5 (3 и 5 клеток).

Рис. 85. Способы построения осей аксонометрических проекций

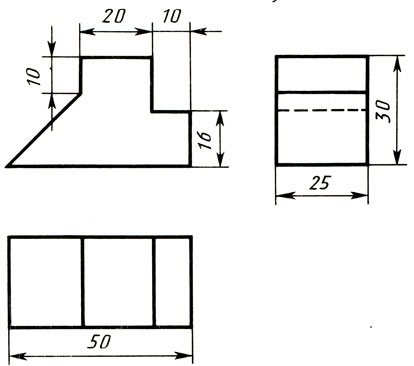
Построение фронтальной диметрической и изометрической проекций. Построить фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 86.

Рис. 86. Комплексный чертеж детали

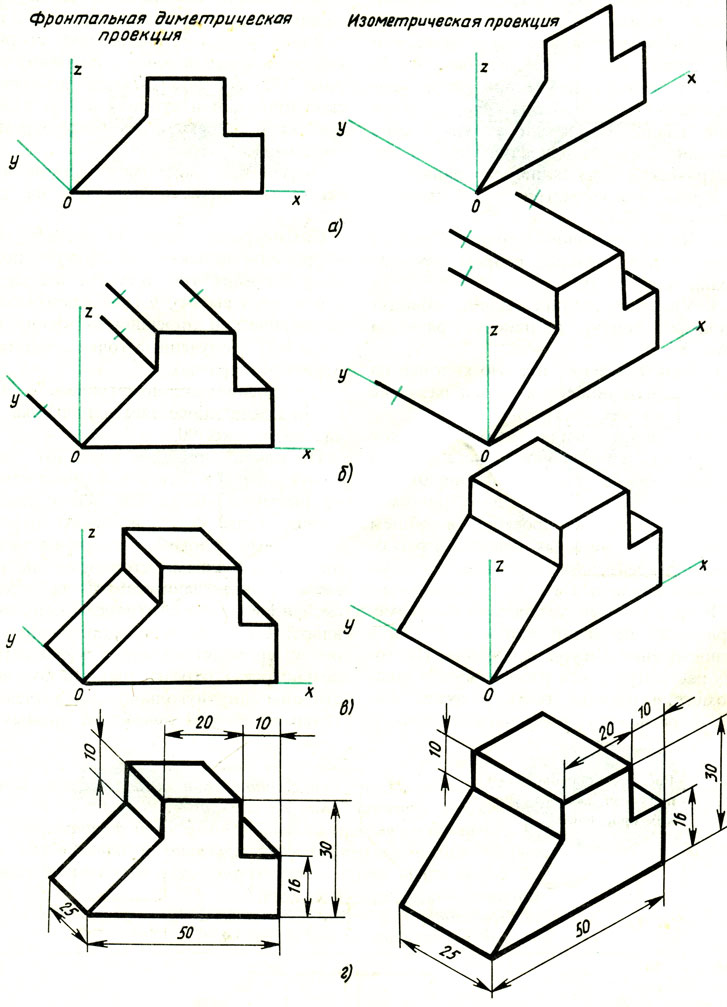
Порядок построения проекций следующий (рис. 87):

1. Проводят оси. Строят переднюю грань детали, откладывая действительные величины высоты — вдоль оси z, длины — вдоль оси х (рис. 87, а).

2. Из вершин полученной фигуры параллельно оси v проводят ребра, уходящие вдаль. Вдоль них откладывают толщину детали: для фронтальной ди-метрической проекции — сокращенную в 2 раза; для изометрии — действительную (рис. 87, б).

3. Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 87, в).

4. Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 87, г).

Сравните левую и правую колонки на рис. 87. Что общего и в чем различие данных на них построений?

Рис. 87. Способ построения аксонометрических проекций

Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод о том, что порядок построения фронтальной диметрической и изометрической проекций в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у.

В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.

Построение аксонометрической проекции квадрата показано на рис. 88, а и б.

Вдоль оси х откладывают сторону квадрата а, вдоль оси у — половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми.

Рис. 88. Аксонометрические проекции квадрата: а — фронтальная диметрическая; б — изометрическая

Построение аксонометрической проекции треугольника показано на рис. 89, а и б.

Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у — его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых.

Рис. 89. Аксонометрические проекции треугольника: а — фронтальная диметрическая; б — изометрическая

Построение аксонометрической проекции правильного шестиугольника показано на рис. 90.

По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.

Рис. 90. Аксонометрические проекции правильного шестиугольника: а — фронтальная диметрическая; б — изометрическая

Содержание

Задания к § 13
Презентация «Построение комплексного чертежа цилиндра и его аксонометрической проекции»
Оставьте свой комментарий
Подарочные сертификаты
Как правильно построить цилиндр в положении лёжа?
Построение аксонометрического чертежа цилиндра вращения
📹 Видео

Ответьте на вопросы

1. Как располагают оси фронтальной диметрической и изометрической проекций? Как их строят?

2. Какие размеры откладывают вдоль осей фронтальной диметрической и изометрической проекций и параллельно им?

3. Вдоль какой аксонометрической оси откладывают размер уходящих вдоль ребер предмета?

4. Назовите общие для фронтальной диметрической и изометрической проекций этапы построения.

Задания к § 13

Упражнение 40

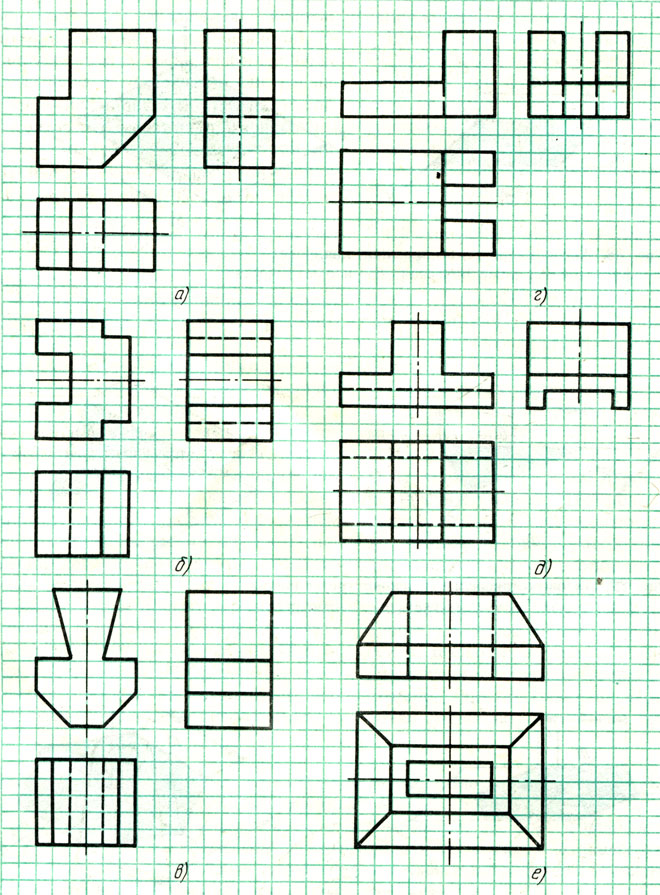
Постройте аксонометрические проекции деталей, приведенных на рис. 91, а, б, в — фронтальные диметрические, для деталей на рис. 91, г, д, е — изометрические.

Размеры определите по числу клеток, считая, что сторона клетки равна 5 мм.

В ответах дано по одному примеру последовательности выполнения заданий.

Рис. 91. За типе на построение аксонометрических проекций

Упражнение 41

Постройте в изометрической проекции правильные четырехугольную, треугольную и шестиугольную призмы. Основания призм расположены горизонтально, длина сторон основания 30 мм, высота 70 мм.

В ответах дан пример последовательности выполнения задания.

Видео:Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать

Презентация «Построение комплексного чертежа цилиндра и его аксонометрической проекции»

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Начертательная геометрия Проецирование цилиндра. Построение комплексного чертежа Построение аксонометрической проекции Определение проекций точек на поверхности цилиндра

Построение координатных осей X Z Y Y 0

Построение осей симметрии X Z Y Y 0

Построение основания цилиндра X Z Y Y 0 d

Построение фронтальной и профильной проекции цилиндра X Z Y Y 0 d h

Построение круга в изометрии Точки А- являются центрами больших дуг овала Точки В – это центры малых дуг овала Точки 1,2,3,4-это точки сопряжения A A R=d/2 B B 0 X Y 1 2 3 4

Аксонометрическое изображение цилиндра Z Y X Y 0 d Z1 X1 Y1 h h 01 01 X1 Y1 Z1

Построение точек на поверхности цилиндра Z Y X Y 0 d Z1 X1 Y1 h h a’ ZA a a″ ZA a A 01 X1 Y1 Z1 01

Построение точек на поверхности цилиндра Z Y X Y 0 d Z1 X1 Y1 h h 01 01 X1 Y1 Z1 b’ b b″ ZB XB XB b ZB B

Построение точек на поверхности цилиндра Z Y X 0 d Z1 X1 Y1 h h 01 01 X1 Y1 Z1 b’ b b″ ZB XB XB b ZB B (f’) f f″ ZF F

Международная дистанционная олимпиада Осень 2021

Вам будут интересны эти курсы:

Оставьте свой комментарий

Школьников не планируют переводить на удаленку после каникул

Минобрнауки утвердило перечень олимпиад для школьников на 2021-2022 учебный год

Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников

В школе в Пермском крае произошла стрельба

Минобрнауки работает над изменением подходов к защите диплома

Минпросвещения планирует прекратить прием в колледжи по 43 профессиям

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Читайте также: Hr16de блок цилиндров ремонт

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Как начертить цилиндр в объемеСкачать

Как правильно построить цилиндр в положении лёжа?

1) Сначала намечаем соотношения пропорций и наклон цилиндра.

2) Представляем цилиндр, находящимся внутри описываемой вокруг него коробки.

3) Намечаем основные направляющие в соответствии с законом линейной перспективы (параллельные линии сходятся в одну точку на линии горизонта).

4) Проверяем соотношения и наклоны направляющих в передней и дальней фронтальных плоскостях коробки. Именно сюда мы будем вписывать эллипсы.

5) Находим диагонали в данных плоскостях.

6) Находим вертикальную и горизонтальную оси. Построение напоминает подготовительную разметку для рисования эллипса в горизонтальном положении.

7) Намечаем границы эллипса: он будет слегка искажён в соотношении с осями симметрии. Это нормально, так как плоскость, в которую эллипс вписан, тоже слегка видоизменена, вытянута по диагонали.

8) Дальний эллипс выглядит более “круглым”, по сравнению с передним. Это происходит потому, что пропорции дальней плоскости немного видоизменены по сравнению c ближайшей из-за подчинения направляющих объекта линейной перспективе. Так и должно быть, не пугайтесь, но от сильного искажения лучше избавиться. Как правило, у небольших по размеру объектов искажение едва уловимо глазом.

Если вам хочется ещё лучше научиться рисовать базовые формы, у нас есть для вас:

Смело нажимайте на ссылку.

Если вам понравилась эта статья, сделайте следующее:

2. Поделитесь этим постом с друзьями в социальных сетях или своём блоге.

3. И конечно же, оставьте свой комментарий ниже ?

Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Построение аксонометрического чертежа цилиндра вращения

Построение прямоугольной изометрической проекции рассматриваемого цилиндра с учётом ранее выполненной привязки этой фигуры к прямоугольной системе координат Оxyz (см. рисунок 3.2) начнём с изображения аксонометрических осей (см. рисунок 2.4) на отдельном листе ватмана формате А3 или А4.

Далее построим аксонометрическую проекцию окружности верхнего основания цилиндра. Такой проекцией является эллипс, имеющий следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, — где d — диаметр изображаемой окружности. Малая ось эллипса всегда располагается вдоль «свободной» координатной оси. «Свободной» называют координатную ось, перпендикулярную плоскости, в которой расположена изображаемая окружность. В рассматриваемом примере окружности оснований цилиндра располагаются в плоскостях, параллельных П₁ и «свободной» является ось Oz.

Сначала графически определим размеры осей эллипса. Известно, что в прямоугольной изометрической проекции размер малой оси эллипса равен длине стороны квадрата, вписанного в изображаемую окружность. Поэтому на виде сверху чертежа цилиндра построим такой квадрат (рисунок 3.7) и определим длину отрезка t – половины стороны квадрата. В последующем для упрощения построений при определении на ортогональном чертеже длины отрезка t будет использована лишь линия, расположенная под углом 45° к координатным осям (без изображения квадрата целиком).

Далее на аксонометрическом чертеже (рисунок 3.8), по «свободной» оси O¢z¢, в обе стороны от начала координат О¢ отложим отрезок t и получим точки B¢ и D¢, определяющие малую ось эллипса. Для нахождения точек А¢ и С¢, определяющих большую ось эллипса, из найденных точек B¢ и D¢, как из центров,построим две дуги радиуса R=2t до их взаимного пересечения. Соединяя найденные точки между собой, определим большую ось эллипса.

Построим вместо эллипса овал — замкнутую кривую, представляющую собой четыре последовательно сопряжённые дуги окружностей радиуса R и r. Для этого сначала определим центры этих дуг (рисунок 3.9). Центры О 1 и О 2 дуг радиуса R определим на оси O¢z¢ в точках пересечения её с окружностью радиуса, равного большой полуоси эллипса, а центры О 3 и О 4 дуг радиуса r определяем в точках пересечения большой оси эллипса с окружностью радиуса, равного малой полуоси эллипса. После этого определяются и радиусы дуг:
R =О 1 В¢ = О 2 D¢; r = О 3 А¢ = О 4 С¢ (рисунок 3.10). Далее из найденных центров О 1 , О 2 , О 3 , О 4 циркулем строим четыре сопряжённые дуги овала. Напомним, что точка сопряжения двух дуг располагается на прямой, проходящей через центры этих дуг. Например, точка N сопряжения нижней дуги радиуса R с левой дугой радиуса r находится на прямой, проходящей через центры

О 2 и О 3 рассматриваемых дуг.

Аксонометрию нижнего основания цилиндра строим смещением вниз на величину h центров О 1 , О 2 , О 3 , О 4 дуг овала верхнего основания (рисунок 3.11). Далее строим ¼ часть выреза цилиндра и изображаем фронтальную вторичную проекцию призматического отверстия, образованного плоскостями a, b и g (рисунок 3.12). Размеры a, b и с, необходимые для этого переносим на аксонометрический чертёж из ортогонального чертежа (см. рисунок 3.2) параллельно соответствующим аксонометрическим осям.

Обозначим через m¢ и n¢ аксонометрические очерковые образующие цилиндра (рисунок 3.13) и построим их фронтальные вторичные проекции m¢₂ и n¢₂ (последовательность построений показана стрелками). Далее отметим точки 1₂¢, 2₂¢, 3₂¢, 4₂¢ — пересечение линий фронтальной вторичной проекции отверстия в цилиндре с фронтальными вторичными проекциями линий аксонометрического очерка и находим точки 1¢, 2¢, 3¢, 4¢ разрыва линий m¢ и n¢ — аксонометрических очерковых образующих конуса граничными линиями отверстия в нём (рисунок 3.14).

Строим в аксонометрии граничные линии отверстия. Для этого сначала на вторичной фронтальной проекции отверстия находим промежуточные точки (рисунок 3.15), используя размеры g и f, перенесённые из ортогонального чертежа (см. главный вид на рисунке 3.2).С помощью указанных вторичных проекций строим аксонометрические проекции промежуточных точек, расположенных на граничных линиях отверстия в цилиндре. Последовательность построения этих точек показана на рисунке 3.16 стрелками. Отрезки, длины которых использованы при по строении аксонометрических

проекций промежуточных точек, помечены штрихами на рисунках 3.2 и 3.16. Соединяя полученные точки, плавной кривой, получим изображения тех граничных линий отверстия в цилиндре, которые формируются плоскостью g. Эти линии помечены на рисунке 3. 16 стрелками А и Б. Аналогично можно построить точки и изображение граничной линии отверстия, формируемой плоскостью b. Однако основная часть этих точек не видна и поэтому не требуется их построение.

Строим овал, определяющий горизонтальную часть призматического отверстия в цилиндре, формируемую плоскостью a (рисунок 3.17). Для этого можно использовать дуги R и r овала верхнего основания конуса, найдя новые центры этих дуг. У построенного овала сохраняем лишь те его участки, которые видны в аксонометрии.

Для окончательного оформления аксонометрического чертежа цилиндра наносим штриховку тех элементов выреза цилиндра, которые располагаются в плоскостях хОz и уОz (рисунок 3.18). Определить направление линий штриховки в аксонометрии по указанным координатным плоскостям можно следующим образом (рис. 3.19). Построим окружность произвольного радиуса с центром в начале координат и соединим между собой точки пересечения этой окружности с координатными осями, определяющими рассматриваемые плоскости. Построенные отрезки и определят направления линий штриховки по указанным плоскостям.

Читайте также: Задний тормозной цилиндр туксон 2008

Подчеркнём, что окончательное оформление аксонометрического чертежа рассматриваемого цилиндра требует плавного соединения всех полученных точек при изображении сквозного отверстия и обводку всех видимых линий контура изображения цилиндра.

3.4. Построение ортогонального и аксонометрического чертежей
конуса вращения

Переходим к рассмотрению в задаче 2 построения ортогонального и аксонометрического чертежей конуса вращения.

На рисунке 3.20 показаны изображения: главный вид и частично вид сверху прямого кругового усечённого конуса, а также габаритный прямоугольник для последующего построения вида слева.

Рассматриваемый конус имеет сквозное отверстие, образованное тремя плоскостями: горизонтальной плоскостью a, рассекающей коническую поверхность по окружности, и двумя фронтально проецирующими плоскостями b и g, рассекающими его поверхность по эллипсам.

Для построения видов сверху и слева, а также аксонометрического изображения данного конуса осуществим привязку этой фигуры к прямоугольной системе координат Оxyz (рисунок 3.21). В качестве горизонтальной координатной плоскости выберем плоскость нижнего основания конуса.

На главном виде отмечаем характерные и промежуточные точки граничных линий отверстия и выполняем их построение на виде сверху.

Сначала рассмотрим точки 1, 2, 3, расположенные на горизонтальных граничных линиях отверстия, формируемых плоскостью a (см. рисунок 3.21). Эти точки (всего их шесть) определяем на виде сверху по линиям связи на окружности радиуса R. Указанный радиус измеряем на главном виде, в плоскости a от оси конуса до его очерковой образующей.

Аналогично определяем горизонтальные проекции точек 4, 5 и 6 граничных линий отверстия, расположенных в плоскости b (рисунок 3.22). Для этого строим окружности радиуса R 1 , R 2 и R 3 , расположенные в промежуточных горизонтальных плоскостях a 1 , a 2 , a 3 .

Аналогично строим на виде сверху точки граничных линий отверстия, расположенных в плоскости g. Последовательно соединяем найденные горизонтальные проекции точек плавными кривыми. Окончательное оформление вида сверху показано на рисунке 3.23. Здесь линиями невидимого контура показаны линии пересечения плоскостей a и b, g и b, a и g.

Построение профильных проекций рассматриваемых точек (см. рисунок 3.23) осуществляем как по линиям связи (точки 3₃ и 6₃) на линиях профильного очерка конуса, так и переносом отрезков ординат точек с вида сверху на вид слева. Переносимые отрезки показаны одинаковыми символами как на виде сверху, где они измеряются, так и на виде слева, где они откладываются. Последовательно соединяем найденные профильные проекции точек

плавной кривой, а также изображаем линии невидимого контура, определяющие линии пересечения плоскостей a и b,
g и b, a и g.

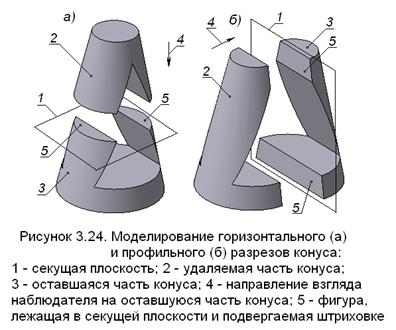
Далее строим горизонтальный и профильный разрезы конуса. Моделирование горизонтального и профильного разрезов конуса, имеющего сквозное отверстие, показано на рисунке 3.24. Изображение горизонтального разреза выполняем на виде сверху, а профильного – на виде слева (рисунок 3.25). В обоих случаях совмещаем половину соответствующего вида с половиной разреза, используя вертикальную осевую линию в качестве границы между этими изображениями. На совместном изображении разрезы располагаем справа от границы, а виды слева от неё. Производим обозначение горизонтального разреза. После построения на чертеже необходимых разрезов на всех его изображениях удаляем линии невидимого контура.

Более подробная информация о правилах построения и обозначения разрезов в соответствии с ГОСТ 2.305 – 68 приведена в разделе 3.2.

Построим прямоугольную изометрическую проекцию рассматриваемого конуса, используя привязку к нему ортогональной системы координат Оxyz, выполненную ранее (см. рисунок 3.21). На отдельном листе ватмана формата А3 или А4 изобразим аксонометрические оси (см. рисунок 2.4).

Далее построим аксонометрические проекции окружностей нижнего и верхнего оснований конуса. Такими проекциями будут два эллипса, центры которых располагаются на координатной оси O¢z¢ и смещены относительно друг друга на расстояние h (рисунок 3.26). Эллипсы имеют следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, — где d — диаметр изображаемой окружности. Малая ось эллипсов располагается вдоль «свободной» координатной оси O¢z¢, а её размер равен длине стороны квадрата, вписанного в изображаемую окружность.

Для удобства построений вместо эллипсов изображаем овалы (см. рисунки 3.9 и 3.10). При этом используем графическое определение как малых полуосей эллипсов (см. на рисунке 3.20, на виде сверху отрезки t и t¢ ), так и больших полуосей (см. рисунок 3.8).

Далее строим прямые m¢ и n¢, являющиеся аксонометрическим очерком конической поверхности (рисунок 3.27). При этом определяем точки касания этими линиями эллипсов, являющихся основаниями конуса. Для этого удлиняем образующие а¢ и b¢ до точек А¢ и В¢ пересечения этих линий с верхним основанием конуса. Образующие а¢ и b¢ вместе с осевой линией чертежа образуют три прямые, проходящие через вершину конyса. Эта вершина на чертеже недоступна. Указанные три прямые пересекают эллипсы (овалы) оснований в шести точках. Соединяем точки пересечения с овалом смежных прямых крест на крест, а через точки их пересечений (см., например точки С¢ и D¢ ) проводим прямые до пересечения с эллипсами (см. точки E¢, F¢, Q¢, L¢). Найденные точки нижнего и верхнего оснований конуса соединяем отрезками прямых. Это и будут линии аксонометрического очерка конуса.

Затем выполняем вырез ¼ части конуса и строим фронтальную вторичную проекцию призматического отверстия в конусе, т. е. по

существу строим фронтальные вторичные проекции плоскостей a, b и g, формирующих отверстие в конусе (рисунок 3.28). При этом размеры a, b и c из ортогонального чертежа (см. главный вид на рисунке 3.23) переносим на аксонометрический чертёж параллельно соответствующим аксонометрическим осям.

Далее необходимо построить точки 1¢, 2¢, 3¢ и 4¢ разрыва линий аксонометрического очерка конуса граничными линиями отверстия в нём. Однако перед этим предварительно определим их фронтальные вторичные проекции 1₂¢, 2₂¢, 3₂¢, 4₂¢ (рисунок 3.29). Для этого сначала строим фронтальные вторичные проекции m₂¢, n₂¢ очерковых образующих конуса и находим точки пересечения этих проекций с линиями вторичной проекции отверстия. Последовательность этих построений показана стрелками. При этом подчеркнём, что построения начинаются не в конечных точках больших осей эллипсов (овалов), а в граничных точках E¢, F¢, Q¢, L¢ аксонометрических очерковых образующих, построенных ранее. Далее находим искомые точки 1¢, 2¢, 3¢ и 4¢ (рисунок 3.30).

Строим аксонометрические проекции промежуточных точек граничных линий отверстия. Для этого сначала на линиях фронтальной вторичной проекции отверстия намечаем промежуточные точки (рисунок 3.31). При этом используем размеры g и f, перенося их из ортогонального чертежа (см. рисунок 3.23). Далее через найденные вторичные проекции проводим прямые, параллельные оси О¢у¢, и откладыванием на них в обе стороны ординаты искомых точек (рисунок 3.32). Ординаты промежуточных точек, помеченные штрихами, переносим из ортогонального чертежа (см. рисунок 3.23) на аксонометрический чертёж. При этом изображаем лишь точки, видимые на аксонометрическом чертеже. Последовательно соединяя найденные точки плавными кривыми (дугами эллипсов), строим видимые участки граничных линий отверстия в конусе, формируемые плоскостью b (см. на рисунке 3.32 линии А и Б) и плоскостью g (см. линию В).

Строим овал, определяющий граничные линии горизонтальной части отверстия в конусе и формируемые плоскостью a (рисунок 3.33). Границы видимости условно показаны стрелками. Изображаем прямую, являющуюся линией пересечением плоскостей a и g.

Выполняем штриховку участков конуса, расположенных в координатных плоскостях хОz и уОz. Определение направлений линий штриховки в прямоугольной изометрии показано на рисунке 3.19.

Читайте также: Цилиндр подъема кузова газ 53 установка

Окончательное оформление аксонометрического чертежа конуса со сквозным отверстием (рисунок 3.34) требует тщательной обводки всех линий изображения: дуги овалов обводятся циркулем, а другие кривые – с помощью лекала.

4. Построение ортогонального и аксонометрического чертежей детали
(третья задача)

Планировка листа и построение изображений детали по размерам, нанесённым на эти изображения в индивидуальном задании, показаны на рисунке 4.1. Изображения включают в себя: главный вид, вид сверху, а также габаритный прямоугольник для дальнейшего построения вида слева.

Для построения вида слева и аксонометрического чертежа детали осуществим привязку детали к прямоугольной системе координат Оxyz (рисунок 4.2). За горизонтальную координатную плоскость примем плоскость верхнего основания цилиндрической плиты, срезанной по бокам двумя фронтальными плоскостями, и имеющей два полуовальных выреза. На этой плите расположен цилиндр вращения, ось которого совпадает с координатной осью Оz. Его подкрепляют два ребра жёсткости – призматические элементы треугольной формы. Внутренняя форма детали состоит из сквозного ступенчатого цилиндрического отверстия.

При построении вида слева особый интерес представляет построение дуги эллипса, образованного пересечением цилиндра с наклонной гранью ребра жёсткости. Построение выполнено по трём точкам (1, 2 и 2) путём переноса с вида сверху на вид слева ординаты точек 2 и 2, равной полуширине ребра жёсткости (см. размер b/2). Точка 1 в принятой системе координат имеет нулевую ординату.

В третьей задаче кроме видов необходимо построить фронтальный и профильный разрезы детали. Так как рассматриваемая деталь имеет две плоскости симметрии: фронтальную и профильную, — и по этим плоскостям выполняется её рассечение, то положение секущих плоскостей на чертеже не указываем, а разрезы совмещаем с половинами соответствующих видов (рисунок 4.3). Границей между этими изображениями является ось симметрии (штрих пунктирная линия). Вид оставляем слева от осевой линии, а разрез помещаем справа от этой линии. При выполнении разрезов удаляем все линии, изображающие внешнюю форму детали, а линии невидимого контура (штриховые линии) заменяем сплошными основными линиями. На всех видах удаляем штриховые линии. Контуры детали, расположенные в секущих плоскостях, заштриховываем тонкими параллельными линиями, расположенными под углом 45° к линиям основной надписи чертежа. Направление штриховки должно быть одинаковым для всех выполненных разрезов. Рекомендуется соблюдать интервал штриховки, равный 2,5 … 3 мм.

Обращаем внимание на условность, принятую в машиностроительном черчении, — при продольном разрезе ребра жёсткости его контур не заштриховывается. Более подробная информация о разрезах приведена в подразделе 3.2.

Построение прямоугольной изометрической проекции рассматриваемой детали с учётом привязки её к прямоугольной системе координат, выполненной ранее (см. рисунок 4.2), начнём с изображения аксонометрических осей (см. рисунок 2.4) на отдельном листе ватмана формата А3 или А4.

Напомним, что круглое основание любого цилиндрического или конического элемента детали, расположенное в координатной плоскости или параллельно такой плоскости, в прямоугольной изометрии изображается эллипсом, имеющим следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, — где d — диаметр изображаемой окружности. Малая ось эллипсов располагается вдоль «свободной» координатной оси, — оси, перпендикулярной плоскости, в которой расположена изображаемая окружность,а размер малой оси равен длине стороны квадрата, вписанного в изображаемую окружность. Для удобства построения и получения лучшего качества изображения на аксонометрическом чертеже вместо эллипсов строим овалы – циркульные кривые (см. рисунки 3.9 и 3.10). Поэтому сначала строим овалы, определяющие горизонтальные вторичные проекции всех цилиндрических элементов детали (рисунок 4.4). Для графического определения малых полуосей эллипсов используем построения, показанные на рисунке 4.3 (см. размер а и отрезки, помеченные штрихами). Размеры b, c, m и n, используемые для построений, переносим с ортогонального чертежа (см. рисунок 4.2).Далее строим прямые, определяющие горизонтальные вторичные проекции плоских элементов детали (рисунок 4.5). На следующем этапе построения аксонометрии удаляем ненужные линии чертежа с учётом выполнения в дальнейшей выреза ¼ детали (рисунок 4.6).

Далее создадим объёмное изображение основания детали (рисунок 4.7). Для этого из точек горизонтальной вторичной проекции основания детали, расположенных ближе к наблюдателю, строим вспомогательные прямые, параллельные оси О¢ z¢, и на них откладываем вниз отрезки длиной t, определяющей толщину плиты основания. Таким образом, определяем точки контура нижней части основания. Изображения плоских участков основания выполняем лишь по их граничным точкам, а для цилиндрических участков строим и промежуточные точки. Длину отрезка t определяем на ортогональном чертеже (см. рисунок 4.2). Соединяя найденные точки нижней плоскости основания прямыми или плавными кривыми и удаляя ненужные вспомогательные вертикальные отрезки, построим основание детали.

Аналогично с помощью вспомогательных вертикальных отрезков длиной Н, используя горизонтальные вторичные проекции цилиндрических элементов, можно построить точки верхнего основания этих элементов детали (рисунок 4.8). Найденные точки соединяем плавными кривыми, а вспомогательные вертикальные отрезки и невидимые линии чертежа удаляем. Для построения изображения рёбер жёсткости находим точки 1¢ и 2¢ (рисунок 4.9). Для этого из соответствующих точек горизонтальных вторичных проекций рёбер строим вспомогательные вертикальные отрезки длиной е и f. Длины этих отрезков измеряем на ортогональном чертеже (см. рисунок 4.2). Строим лишь видимые элементы рёбер, а невидимые удаляем.

Удалив все невидимые линии чертежа, включая вторичные проекции цилиндров и рёбер жёсткости, построенные ранее, приступаем к изображению элементов нижней части ступенчатого цилиндрического отверстия (рисунок 4.10). Построение нижней видимой части окружности цилиндрического отверстия меньшего радиуса осуществляем с помощью вспомогательных вертикальных отрезков длиной h, проведенных вниз из пяти точек верхнего основания этого отверстия. Три из пяти построенных точек соединяем плавной кривой.

Для изображения в аксонометрии видимой части окружности радиуса r цилиндрического углубления, расположенного в нижней части детали, строим образующие этой цилиндрической поверхности, попадающие в вырез ¼ части детали и овал, соответствующий окружности цилиндрического углубления, расположенной в нижней плоскости основания детали (см. на рисунке 4.10 овал, изображённый штриховой линией). У построенного овала сохраняем лишь его видимую часть, показанную на рисунке 4.10 стрелкой.

В заключение производим обводку чертежа и наносим штриховку (рисунок 4.11). Определение направлений линий штриховки в аксонометрии показано на рисунке 3.19.

Окончательное оформление аксонометрического чертежа детали требует плавного (с помощью лекал) соединения построенных точек кривых линий, изображающих как элементы сквозного ступенчатого цилиндрического отверстия в детали, так и элементы её внешней формы. Завершается оформление чертежа заполнением его основной надписи.

Окончательно оформленные ортогональный и аксонометрический чертежи детали показаны соответственно на рисунках 4.12 и 4.13.

Отметим также, что во всех рассмотренных ранее построениях измерение размеров на ортогональном чертеже и перенос их на аксонометрический чертеж производилось с помощью измерителя.

На изображениях ортогонального и аксонометрического чертежей рекомендуется сохранять характерные и вспомогательные точки построенных линий, без обозначения этих точек.

1. Единая система конструкторской документации. Общие правила выполнения чертежей. М., 1991,453 с.

2. Аверин В.Н., Куколева И Ф. Нанесение размеров на чертежах. Методические указания к практическим занятиям по инженерной графике. М.: МИИТ, 2008. 37 с.

3. Аверин В.Н., Пуйческу Ф.И. Прямоугольная изометрическая проекция. Методические указания к практическим занятиям по инженерной графике. М.: МИИТ, 2008. 23 с.