Как строить усеченный цилиндр в изометрии

Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Развертка усеченного цилиндра. Построение развертки цилиндра.

Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Развертка усеченного цилиндра. Построение развертки цилиндра.

Проекция цилиндра, срезанного плоскостью, наклонной к плоскости чертежа, по вертикальной плоскости проекции дает прямую линию, на горизонтальной — окружность, на профильной плоскости — замкнутую кривую, эллипс в искаженном виде.

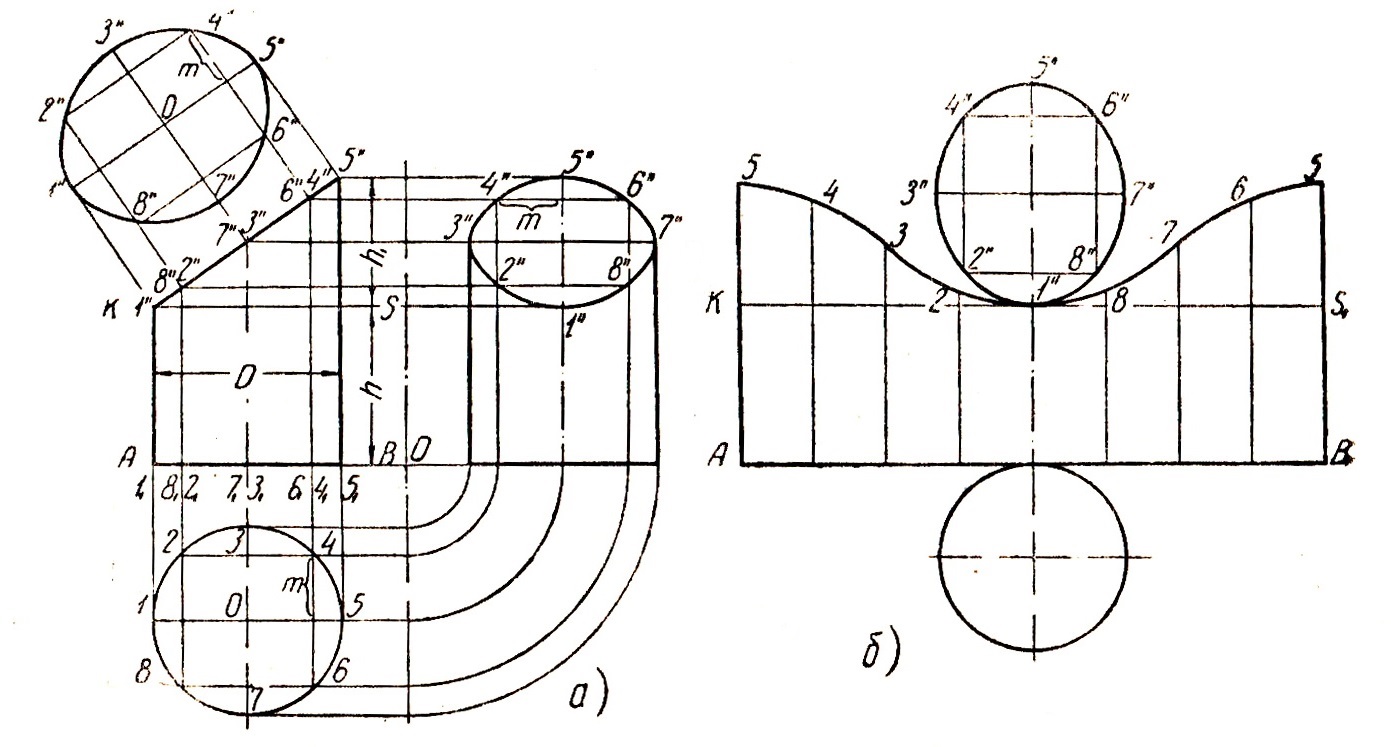
Если представить себе цилиндр, срезанный плоскостью KS (рис. 1, а), параллельной основанию и проходящей через низшую точку наклонного среза 1, то нижняя часть такого цилиндра развернется в прямоугольник A₁K₁S₁B₁ (рис. 1, б) с высотой h = BS и основанием А₁В₁ = πD.

Рис. 1. Развертка усеченного цилиндра:

а — проекция; б — развертка.

Развертка верхней части цилиндра.

Чтобы получить развертку верхней части цилиндра выше плоскости KS, поступают следующим образом. Окружность основания делится на несколько равных частей, в приведенном примере на- восемь равных частей. Точки делений проектируют на вертикальную проекцию и проводят соответствующие образующие цилиндра 1₁ — 1′; 2₁ — 2″ и т. д. Затем делят длину развернутой окружности основания на такое же число равных частей, и из точек делений восстанавливают перпендикуляры, которые будут представлять собой те же образующие цилиндра, на которых затем нужно отложить их длины, измеряя одноименные отрезки на вертикальных проекциях (рис. 1, б). Соединив плавной кривой полученные точки, будем иметь развертку боковой поверхности усеченного цилиндра.

Для определения действительной формы поперечного сечения наклонной поверхности цилиндра вводят дополнительную плоскость проекции, параллельную плоскости сечения, на которой форма сечения спроектируется в искаженном виде — в форме эллипса.

Построение сечения цилиндра.

Для построения сечения на дополнительной плоскости проведем линию, параллельную проекции плоскости сечения, и, спроектировав на нее точки 1″ и 5″ с вертикальной проекции, получим большую ось эллипса. Затем из точки 7″ — 3″ на вертикальной проекции проведем линию, перпендикулярную большой оси эллипса, и, отложив на ней вправо и влево от большой оси отрезки 03″ и 07″, равные радиусу основания цилиндра, получим малую ось эллипса 3″ — 7″.

Положение остальных точек 2″, 4″, 6″, 8″ определяется так: на перпендикулярах к большей оси, проведенных из точек 8″ — 2″ и 6″ — 4″ вертикальной проекции, откладываем отрезки m от большей оси эллипса. Плавная кривая, проведенная через полученные восемь точек, будет эллипсом.

Построение эллипса на профильной проекции видно из рис. 1, а.

Для получения полной развертки поверхности цилиндра следует добавить поверхности наклонного сечения и нижнего основания цилиндра, как указано на рис. 1, б.

Читайте также: Главный тормозной цилиндр my summer car

Видео:Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

Урок 7. Сечение цилиндра плоскостью. Развертка усеченного цилиндра

Здравствуйте друзья! На этом уроке мы будем строить сечение цилиндра плоскостью и развертку усеченного цилиндра.

За основу возьмем модель цилиндра, построенного на втором уроке по 3d моделированию.

Видео:Построение изометрии усеченного цилиндра │Урок #60Скачать

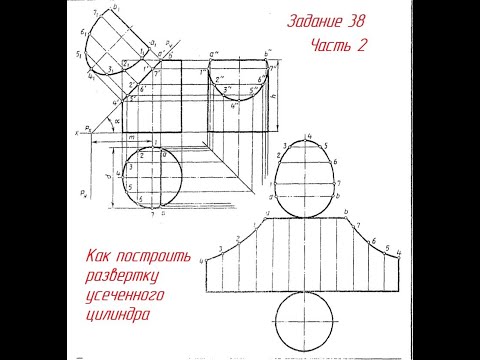
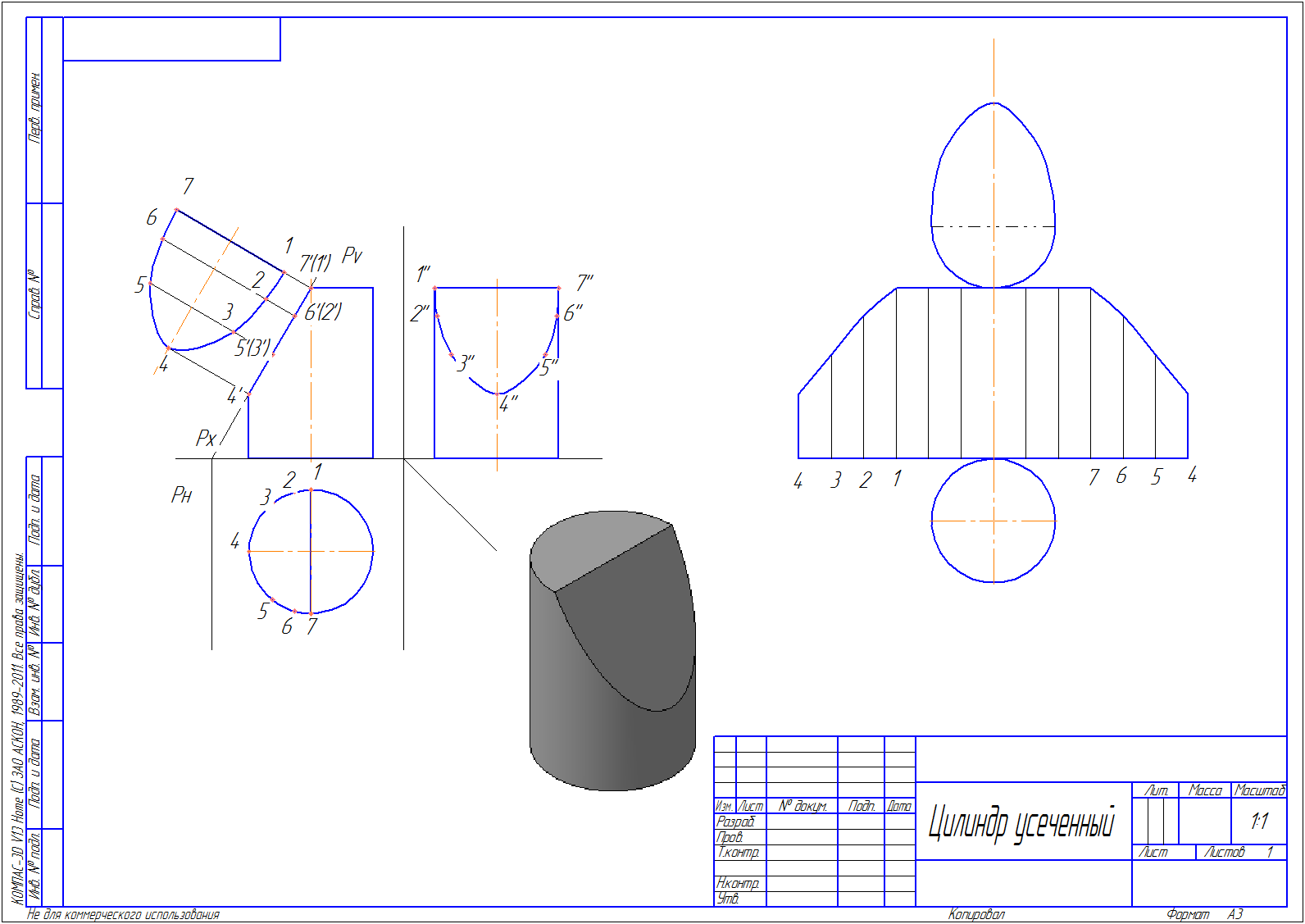
Последовательность построения усеченного цилиндра

Пункты 1 — 4 аналогичны пунктам построения чертежа усеченной призмы .

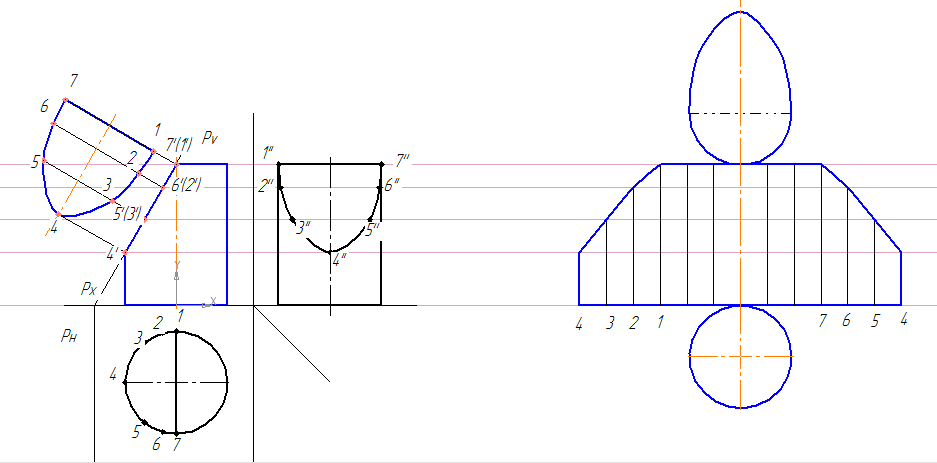
5. От оси симметрии цилиндра откладываем расстояние до следа секущей плоскости – 32 мм, проводим след секущей плоскости Pv под углом 60º.

6. Обозначаем несколько точек пересечения поверхности цилиндра со следом плоскости. Находим их на проекциях цилиндра. Соединяем точки при помощи кривой Безье. Получаем искаженные фигуры сечений.

7. Построим натуральный вид сечения

Построение натурального вида сечения цилиндра

8, 9 Построение аналогично построению сечения призмы

Развертка усеченного цилиндра

10. Развертку цилиндра будем строить на одной линии с осями x и y1.

11. Откладываем отрезок длиной l=π*D=3,14*40=125,6 мм.

12. Делим этот отрезок на 12 равных частей, нумеруем.

13. Переносим высоты отрезков с фронтальной проекции цилиндра. Соединяем полученные вершины при помощи кривой Безье. Натуральный вид сечения переносим копированием и поворотом. Достраиваем нижнее основание цилиндра.

Построение изометрии цилиндра

14. Наглядное изображение цилиндра сделаем при помощи рисунка. Для этого необходимо пересечение плоскостью цилиндра (3d модели).

15. Открываем деталь, в дереве модели выбираем плоскость xy. Строим эскиз, показанный на рисунке.

16. На компактной панели выбираем команду «Сечение по эскизу» . Задаем направление отсечения – прямое. Пересечение цилиндра плоскостью готово.

17. Сохраняем деталь в формате рисунка и вставляем его в чертеж. Оформляем чертеж.

Для лучшего понимания материала советую посмотреть небольшое видео по теме.

Как видите, построение сечения цилиндра плоскостью и развертки усеченного цилиндра, не такая уж и сложная задача вообще, а в Компасе построение идет гораздо проще.

Видео:Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать

Развертка усеченного цилиндра. Построение развертки цилиндра.

Видео:Как начертить цилиндр в объемеСкачать

Развертка усеченного цилиндра. Построение развертки цилиндра.

Проекция цилиндра, срезанного плоскостью, наклонной к плоскости чертежа, по вертикальной плоскости проекции дает прямую линию, на горизонтальной — окружность, на профильной плоскости — замкнутую кривую, эллипс в искаженном виде.

Если представить себе цилиндр, срезанный плоскостью KS (рис. 1, а), параллельной основанию и проходящей через низшую точку наклонного среза 1, то нижняя часть такого цилиндра развернется в прямоугольник A₁K₁S₁B₁ (рис. 1, б) с высотой h = BS и основанием А₁В₁ = πD.

Рис. 1. Развертка усеченного цилиндра:

а — проекция; б — развертка.

Развертка верхней части цилиндра.

Чтобы получить развертку верхней части цилиндра выше плоскости KS, поступают следующим образом. Окружность основания делится на несколько равных частей, в приведенном примере на- восемь равных частей. Точки делений проектируют на вертикальную проекцию и проводят соответствующие образующие цилиндра 1₁ — 1′; 2₁ — 2″ и т. д. Затем делят длину развернутой окружности основания на такое же число равных частей, и из точек делений восстанавливают перпендикуляры, которые будут представлять собой те же образующие цилиндра, на которых затем нужно отложить их длины, измеряя одноименные отрезки на вертикальных проекциях (рис. 1, б). Соединив плавной кривой полученные точки, будем иметь развертку боковой поверхности усеченного цилиндра.

Читайте также: Основной цилиндр сцепления газель

Для определения действительной формы поперечного сечения наклонной поверхности цилиндра вводят дополнительную плоскость проекции, параллельную плоскости сечения, на которой форма сечения спроектируется в искаженном виде — в форме эллипса.

Построение сечения цилиндра.

Для построения сечения на дополнительной плоскости проведем линию, параллельную проекции плоскости сечения, и, спроектировав на нее точки 1″ и 5″ с вертикальной проекции, получим большую ось эллипса. Затем из точки 7″ — 3″ на вертикальной проекции проведем линию, перпендикулярную большой оси эллипса, и, отложив на ней вправо и влево от большой оси отрезки 03″ и 07″, равные радиусу основания цилиндра, получим малую ось эллипса 3″ — 7″.

Положение остальных точек 2″, 4″, 6″, 8″ определяется так: на перпендикулярах к большей оси, проведенных из точек 8″ — 2″ и 6″ — 4″ вертикальной проекции, откладываем отрезки m от большей оси эллипса. Плавная кривая, проведенная через полученные восемь точек, будет эллипсом.

Построение эллипса на профильной проекции видно из рис. 1, а.

Для получения полной развертки поверхности цилиндра следует добавить поверхности наклонного сечения и нижнего основания цилиндра, как указано на рис. 1, б.

Видео:Задание 42. УСЕЧЕННЫЙ КОНУС. Часть 1Скачать

Ортогональные проекции усеченного цилиндра

На рис. 283 изображен прямой круговой цилиндр, лежащий на плоскости H, с основа­ниями, параллельными профильной плоскости проекций W. Этот цилиндр рассечен фронталь­но-проецирующей плоскостью, заданной на рис. 283 двумя следами Р_ѵ и Р_H. Требуется построить линию среза цилиндра на ортого­нальных проекциях, натуральную величину среза, усеченный цилиндр в изометрии и раз­вертку поверхности усеченного цилиндра.

Для построения развертки боковой поверх­ности цилиндра, усеченного плоскостью, и для определения положения промежуточных точек при построении проекций линии среза на поверхности цилиндра проводят дополнитель­ные образующие. На рис. 283 проведено 12 образующих. Для этого на профильной проек­ции проекцию основания цилиндра делят на 12 равных частей и через точки деления строят фронтальные и горизонтальные проекции этих образующих. Прежде чем начать построение линии среза, надо представить себе эту ли­нию. Ранее говорилось о том, что если секущая плоскость пересечет одно основание цилиндра и часть боковой поверхности, то линия пересе­чения будет частью эллипса.

На плоскость V линия среза, лежащая в фронтально-проецирующей плоскости, проеци­руется в отрезок, совпадающий с фронтальной проекцией секущей плоскости Р, т. е. совпадет со следом Р_ѵ, и является натуральной величи­ной длины среза. Отрезки, определяющие ши­рину среза, направлены перпендикулярно плоскости V и проецируются на нее в точки. На горизонтальной и профильной проек­циях фигура среза изобразилась с искажением подлине, а размеры среза по ширине, измеряе­мой отрезками ab; 11, 3; 10, 4; 5, 9; 6, 8; в нату­ральную величину, так как они параллель­ны плоскостям Н и W. На профильной проек­ции фигура среза изобразится как часть круга, а на горизонтальной — как часть плоскости, очерченная эллипсом. Эллипс имеет две оси: большую, расположенную по длине среза (от точки 7 до первой образующей), и малую, расположенную по ширине среза (от точки 4 до точки 10). Малая ось эллипса, полученного при пересечении цилиндра, равна его диаметру. Сначала строят характерные точки а, b, 7, 4 и 10. Для этого с фронтальной проекции на горизонтальную проводят линии проекционной связи от точки 7′, лежащей здесь на верхней крайней образующей, до горизонтальной про­екции этой образующей, совпадающей с осью цилиндра. Фронтальные проекции точек 4 и 10 лежат на фронтальных проекциях двух обра­зующих, совпадающих с осью цилиндра, а на горизонтальной проекции эти образующие бу­дут крайними. От точек 4′ и 10′ опускают ли­нии проекционной связи на плоскость H до пересечения их с крайними образующими в точках 4 и 10. Расстояние между точками А и В переносят линиями проекционной связи на горизонтальную проекцию с профильной от точек а» и b».

Читайте также: Замена заднего тормозного цилиндра рено дастер 4х4 своими руками

Затем на горизонтальной проекции строят промежуточные точки, лежащие на других об­разующих, в том месте, где на фронтальной проекции их пересек след плоскости Р_ѵ. Боко­вая поверхность цилиндра пересеклась с плоскостью Р по кривой линии (части эллипса), а основание — по отрезку прямой линии АВ как линия пересечения двух пло­скостей (секущей плоскости Р и плоскости осно­вания).

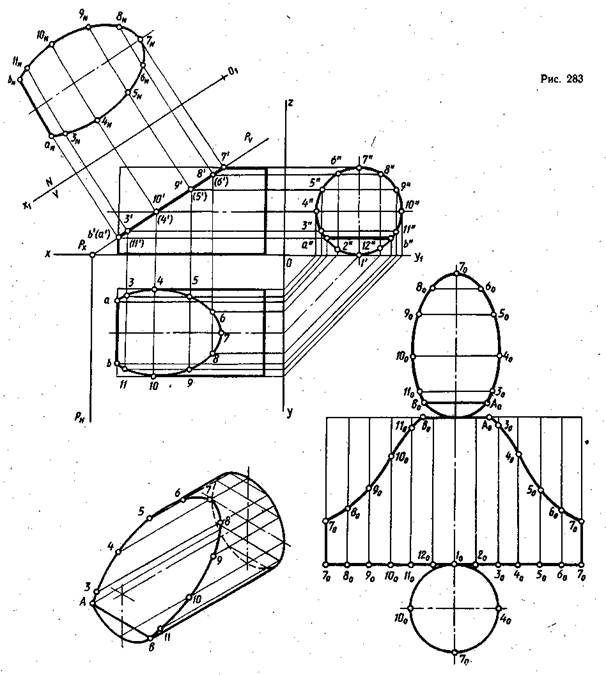Для построения натуральной величины сре­за, фигуры среза, сечение располагают па­раллельно какой-либо плоскости проекций. На рис. 283 это выполнен способом перемены плоскостей проекций. Для этого берется новая плоскость N, перпендикулярная к плоскости проекций V и параллельная плоскости Р. Проек­ция среза на плоскости N изобразится без иска­жения. На чертеже параллельно следу Р_ѵ проводят линию пересечения плоскости V с
плоскостью N, т. е. новую ось О₁х₁ на произ­вольном расстоянии от следа Р_ѵ. Затем от точек а, b, 3 . 11 перпендикулярно оси О₁х₁ проводят линии проекционной связи, перено­сящие расстояния по длине среза с фронталь­ной проекции на новую плоскость N. Для по­ строения отрезков, определяющих ширину сре­за, на горизонтальной проекции измеряют рас­стояния от оси Ох до точек а, b, 3,4, 5 и так да­лее и соответственно откладывают их в новой системе плоскостей от оси О₁х₁. Точки 3_N . 11_N соединяют плавной кривой линией и обводят по лекалу, а точки . a_N и b_N соединяют пря­мой.

🎦 Видео

Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать

Развертка усеченного цилиндраСкачать

Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Построение усеченного цилиндра с сечением в натуральную величинуСкачать

Рисуем усеченный цилиндр.Скачать

Построение изометрии цилиндраСкачать

Как начертить конус в объемеСкачать

Задание 54. Аксонометрия ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 2Скачать

Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

Усеченный конус: проекции сечения, изометрия и развертка поверхностиСкачать

Изометрическая проекция цилиндра. Чертим вместе.Скачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать