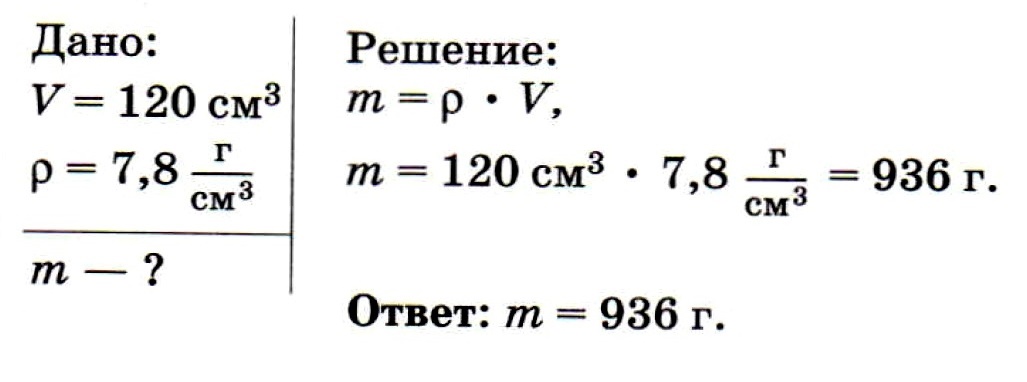Как в физике найти плотность цилиндра (2 видео)

Формулы, используемые в задачах по физике на плотность, массу и объем.

Содержание

Название величины
Обозначение
Единицы измерения
Формула
Масса
m = p * V
Объем
V = m / p
Плотность
кг/м 3
p = m / V
Физика 7 класс: все формулы и определения КРУПНО на трех страницах
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Справочный материал для «Задачи на плотность, массу и объем«
Лабораторная работа 1.01. Определение плотности твердых тел
Кафедра физики
ЛАБОРАТОРНАЯ РАБОТА 1.01
Москва 2005 г.
ТЕОРИЯ ПОГРЕШНОСТЕЙ
Иногда относительная погрешность выражается в процентах:
💡 Видео

Название величины

Обозначение

Единицы измерения

Формула

Масса

m = p * V

Объем

V = m / p

Плотность

кг/м 3

p = m / V

Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

Физика 7 класс: все формулы и определения КРУПНО на трех страницах

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см 3 ?

Задача № 2. Определите объем кирпича, если его масса 5 кг?

Задача № 3. Определите массу стальной детали объёмом 120 см 3

Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м 3 ) меньше плотности стали (ρ₁ = 7800 кг/м 3 ). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

Задача № 5. Определите плотность мела, если масса его куска объемом 20 см 3 равна 48 г. Выразите эту плотность в кг/м 3 и в г/см 3 .

Ответ: Плотность мела 2,4 г/см 3 , или 2400 кг/м 3 .

Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м 2 ?

ОТВЕТ: 160 кг.

РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.

Вычисляем: m = 800 кг/м 3 • 0,04 м 2 • 5 м = 160 кг.

Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

РЕШЕНИЕ: Объем кубика V_K = а 3 = 216 см 3 . Объем стенок V_С можно вычислить, зная массу кубика m_К и плотность меди р: V_С = m_К / р = 91 см 3 . Следовательно, объем полости V_П = V_K — V_C = 125 см 3 . Поскольку 125 см 3 = (5 см) 3 , полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.

Задача № 9 (олимпиадный уровень). Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м 3

РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.

Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

Справочный материал для «Задачи на плотность, массу и объем«

Как, зная только массу, рассчитать плотность?

Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

Читайте также: Что такое стук четвертого цилиндра

Конспект урока «Задачи на плотность, массу и объем с решением».

Видео:Физика 7 класс (Урок№10 - Плотность и масса.)Скачать

Лабораторная работа 1.01. Определение плотности твердых тел

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ «МАМИ»

Видео:Урок 28 (осн). Вычисление массы и объема тела по плотностиСкачать

Кафедра физики

ЛАБОРАТОРНАЯ РАБОТА 1.01

ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЕРДЫХ ТЕЛ

Видео:Расчёт массы и объёма тела по его плотности. Физика 7 классСкачать

Москва 2005 г.

Теория ошибок, определение плотности твердых тел.

В лабораторном практикуме студенты при выполнении работ должны производить измерения, но при использовании даже очень точных и чувствительных приборов и наилучших условий проведения эксперимента во всяком измерении содержится ошибка (погрешность) характер и причины которой могут быть различными. Существуют методы анализа и учета влияния различных погрешностей на результаты измерений. Все погрешности (ошибки) измерений принято подразделять на систематические и случайные.

Систематические ошибки обусловлены постоянными, но односторонними внешними воздействиями. Например, измерение температуры термометром, у которого нулевая точка смешена, будет систематически неправильным, пока в результаты измерений не будет внесена соответствующая поправка.

Так как систематическая ошибка имеет одно и тоже значение, ее нельзя устранить увеличением числа повторных измерений. Но можно уменьшить систематическую ошибку, критически анализируя факторы, которые могут повлиять на результаты, проверяя используемые приборы по соответствующим эталонам, внося поправки в показания приборов, используя более точные приборы и инструменты.

Случайные ошибки при измерениях обусловлены влиянием большого числа факторов, случайным образом изменяющихся в процессе эксперимента. Например, источником случайных ошибок при взвешивании на аналитических весах может явиться неоднородность в распределении температуры в различных частях весов, влияние колебаний стола из-за проезжающего мимо здания грузовика и т. п.

При повторных измерениях случайные ошибки с одинаковой вероятностью приводят к отклонениям значений измеряемых величин от истинного значения как в сторону увеличения, так и в сторону уменьшения, т. е. случайные ошибки имеют разные численные значения и знаки.

Читайте также: Задние тормозные цилиндры пежо 206 седан

Полностью исключить случайные ошибки нельзя, но их можно уменьшить за счет увеличения числа измерений при одних и тех же условиях эксперимента.

Итак, при измерениях неизбежно возникают погрешности. Теория погрешностей указывает на то, как следует вести измерения и их обработку, чтобы допущенные ошибки были минимальными. Кроме того, устанавливаются пределы, внутри которых заключается точное значение определяемой величины.

ТЕОРИЯ ПОГРЕШНОСТЕЙ

I. ПОГРЕШНОСТИ ПРИ ПРЯМЫХ ИЗМЕРЕНИЯХ

Прямыми измерениями называются такие, при которых измерение величины производится непосредственно по шкале прибора. Например,

измерение длины штангенциркулем, измерение веса тела на весах, определение промежутков времени с помощью секундомера. Если отклонение результатов измерений от истинного значения измеряемой величины происходит как в сторону увеличения, так и в сторону уменьшения результатов измерений, то наиболее вероятным значением измеряемой величины будет среднее арифметическое всех сделанных измерений:

где — результаты отдельных измерений, n — число измерений.

Для характеристики степени приближения к истинному значению измеряемой величины вводится понятие абсолютной погрешности — величины, показывающей насколько найденное (среднее арифметическое) значение может отличаться от истинного значения измеряемой величины.

Для определения абсолютной погрешности сначала нужно найти отклонения каждого отдельного измерения от среднего арифметического: , где — отклонение данного измерения, равное разности между средним значением измеряемой величины и результатом этого измерения .

Случайная погрешность вычисляется по формуле:

где — модули отклонений каждого отдельного измерения от среднего арифметического значения.

Из формулы (2) и теории вероятностей следует, что с увеличением числа измерений n случайная погрешность будет уменьшаться.

В качестве систематической погрешности берется приборная погрешность, равная половине цены деления шкалы прибора. Ценой деления прибора называется минимальная величина, измеряемая прибором.

В общем случае необходимо принимать во внимание как случайные, так и систематические погрешности прямых измерений. Поэтому абсолютная погрешность при прямых измерениях рассчитывается по формуле:

где — случайная погрешностей, определяемых по формуле (2),

— систематическая погрешность прибора, инструмента.

Примечание: Если случайная погрешность много меньше систематической, то для повышения точности результата измерений нет смысла увеличивать число измерений, а нужно принять меры к уменьшению систематической погрешности (например, использовать более точные приборы).

Пример. Пусть измеряется диаметр цилиндрического стержня с помощью штангенциркуля и делается 5 измерений: 34.50 мм, 34.65 мм, 34.30 мм,

Среднее арифметическое всех сделанных измерений:

Полученное значение даёт наиболее вероятное значение измеряемой величины D.

Для нахождения случайной погрешности нужно найти абсолютное значение отклонения каждого из 5-ти измерений от среднего арифметического и затем определить среднее значение этих отклонений:

Цена деления штангенциркуля равна 0.05 мм, следовательно, систематическая погрешность равна .

Абсолютная погрешность при измерении диаметра стержня:

Результат измерений принято записывать следующим образом:

(Результат измерений 34,54 мм и абсолютная погрешность 0,12 мм должны заканчиваться в одинаковом разряде)

Для характеристики точности измерения вводится понятие относительной погрешности:

Относительная погрешность ε представляет собой отношение абсолютной погрешности к среднему значению измеряемой величины. В нашем примере относительная погрешность при измерении диаметра:

Относительная погрешность является безразмерной величиной. Она показывает, какую часть измеряемой величины составляет абсолютная погрешность.

Видео:4. Плотность цилиндра. Способ 1Скачать

Иногда относительная погрешность выражается в процентах:

I I. ПОГРЕШНОСТЬ ПРИ КОСВЕННЫХ ИЗМЕРЕНИЯХ.

В большинстве случаев в лабораторном практикуме нельзя определить искомую физическую величину непосредственно по приборам. В этом случае прибегают к косвенным измерениям. Косвенными измерениями являются измерения, полученные на основе прямых измерений и подсчитанные по математическим формулам.

Например, объем цилиндра определяется по формуле , где с помощью прямых измерений определяется диаметр цилиндра D и его высота h, объем же получается в результате косвенных измерений.

Читайте также: Как в блендере обрезать цилиндр

В таких случаях погрешность косвенного измерения зависит не только от погрешностей прямых измерений, но и от вида той математической формулы, по которой находится физическая величина.

Для нахождения погрешностей косвенных измерений удобно воспользоваться правилами дифференциального исчисления, считая искомую величину функцией, а величины, непосредственно измеряемые приборами, ее аргументами. Пусть вид функциональной зависимости определяется формулой , где А — результат косвенного измерения, — результаты прямых измерений. По определению относительная погрешность равна

С другой стороны . Так как погрешность всегда много меньше измеряемой величины А, ошибки можно считать малыми величинами. Это дает возможность замены знака дифференциала d на знак абсолютной ошибки . То есть, можно записать: .

Из сопоставления приведенных формул следует, что относительную погрешность косвенного измерения можно найти путем:

1) логарифмирования исходного выражения ;

2) последующего дифференцирования ;

3) заменой знака дифференциала d на знак абсолютной погрешности ;

4) заменой всех знаков минус на знаки плюс перед знаками абсолютных погрешностей .

Для определения плотности цилиндрического тела применяется формула:

где m — масса тела, D — диаметр, h — высота. Величины m, D, h определяются в результате прямых измерений. Плотность определяется из косвенных измерений. Для нахождения относительной погрешности, выполняем следующие действия:

1) находим натуральный логарифм исходного выражения

2) выполняем дифференцирование : ,

3) заменяем знак d на знак : ,

4) перед всеми знаками ставим знаки плюс .

Далее можно найти абсолютную погрешность: ,

где — абсолютная погрешность косвенного измерения, — среднее значение искомой величины, ε – относительная погрешность.

Иногда в зависимости от расчетной формулы удобнее вначале найти абсолютную погрешность непосредственно, не связывая ее с относительной погрешностью. Для этого используют следующее правило для нахождения абсолютной ошибки при косвенном измерении:

1) дифференцируют исходное выражение;

2) заменяют знак дифференциала d на знак погрешности ;

3) перед всеми знаками ставят знаки плюс.

III. ЗАПИСЬ РЕЗУЛЬТАТА КОСВЕННОГО ИЗМЕРЕНИЯ.

При записи результата косвенного измерения необходимо соблюдать следующие правила:

1. Величину абсолютной погрешности необходимо округлить до двух значащих цифр, если первая из них единица, и до одной во всех остальных случаях (значащими цифрами называются все цифры, кроме нулей, стоящие впереди числа слева). Нули в середине числа и в конце являются значащими. Например, в числе 0.0305 три значащие цифры, в числе 5100 — четыре значащие цифры.

Пример. Если при определении объема цилиндра V абсолютная ошибка оказалась равной , ее следует округлить до двух значащих цифр: . Если , ее следует округлить до одной значащей цифры .

2. Среднее значение измеряемой величины следует записать таким образом, чтобы результат заканчивался в том же разряде, что и абсолютная погрешность.

Пример. Если объем цилиндра при расчете по формуле получается равным , а абсолютная ошибка после округления равна , то объем следует записать также только до десятых

Окончательный результат записывается в виде: .

Такая запись показывает, в каких пределах содержится истинное значение измеряемой величины.

В случае нашего примера для объема цилиндра окончательный результат записывается следующим образом: .

Такая запись указывает, что истинный результат лежит в пределах:

ПРИМЕР ОБРАБОТКИ РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ.

При определении ускорения свободного падения g с помощью математического маятника используется расчетная формула:

где l — длина математического маятника, измеряемая миллиметровой линейкой, n — число колебаний маятника, t — время десяти колебаний маятника, определяемое секундомером. После прямых измерений времени и длины получаем следующие данные:

t = 14.72с, 14.74с, 14.75с, 14.73с, 14.76; n = 10;

1) Результаты измерений заносим в таблицу

Результаты измерений и расчетов. Таблица.