Как вписать фигуру в цилиндр (6 видео)

Содержание

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
Цилиндр, конус, шар
Цилиндр, конус, шар
Теорема Пифагора
Ghenadie Sontu Fine Art
BLOG
Как рисовать цилиндр? Подробная инструкция рисования цилиндра.
💥 Видео

Видео:ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр

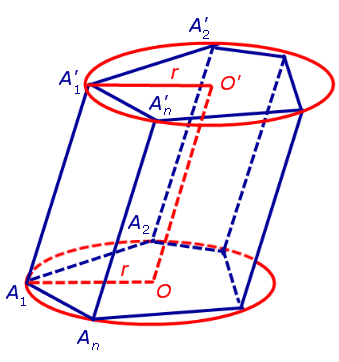
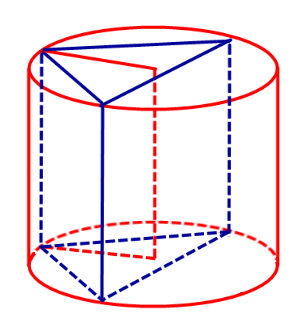
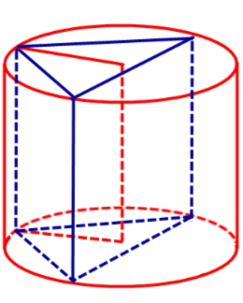
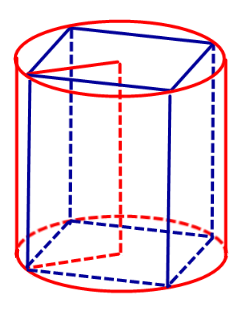
Определение 1. Призмой, вписанной в цилиндр, называют такую призму, основания которой вписаны в окружности оснований цилиндра, а боковые ребра призмы являются образующими цилиндра (рис. 1).

Определение 2. Если призма вписана в цилиндр, то цилиндр называют описанным около призмы.

Прежде, чем перейти к вопросу о том, какую призму можно вписать в цилиндр, докажем следующее свойство призм.

Утверждение 1. Если около оснований призмы можно описать окружности, то отрезок, соединяющий центры описанных окружностей, будет параллелелен и равен боковому ребру призмы.

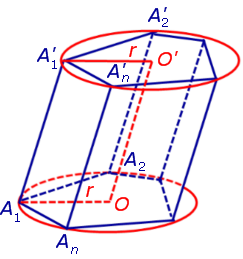
Докажем, что точка O’ является центром окружности радиуса r, описанной около верхнего основания призмы. С этой целью рассмотрим, например, четырехугольник A₁A’₁O’O (рис. 2).

Рассуждая аналогичным образом, заключаем, что

то есть точка O’ – центр окружности радиуса r , описанной около верхнего основания призмы.

В силу того, что четырехугольник OO’A₁A’₁ является параллелограммом, получаем равенство

Теорема. Около призмы можно описать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если около n – угольной призмы описан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, описанного около призмы. Из этого определения также следует, что вписанная в цилиндр призма является прямой призмой, поскольку образующие цилиндра перпендикулярны к плоскостям его оснований,

Таким образом, мы доказали, что, если призма вписана в цилиндр, то оба условия теоремы выполнены.

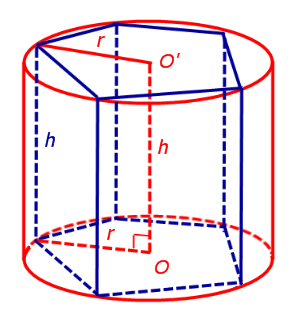
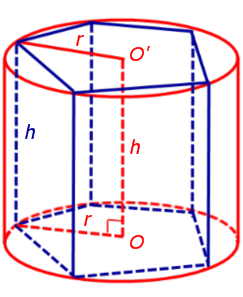
Теперь рассмотрим прямую n – угольную призму высоты h, около оснований которой можно описать окружности, и докажем, что около такой призмы можно описать цилиндр.

Обозначим буквой O центр окружности радиуса r, описанной около нижнего основания призмы, а символом O’ обозначим центр окружности, описанной около верхнего основания призмы.

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет описан около исходной призмы.

Доказательство теоремы завершено.

Следствие 1. Высота призмы, вписанной в цилиндр, равна высоте цилиндра.

Следствие 2. Около любой прямой треугольной призмы можно описать цилиндр (рис. 4).

Следствие 3. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать цилиндр (рис. 5).

Замечание 1. Если у прямоугольного параллелепипеда прямоугольного параллелепипеда три ребра, выходящие из одной вершины, равны a, b, c и различны, то существует три возможности описать около этого параллелепипеда цилиндр в зависимости от того, какое из ребер параллелепипеда выбрано в качестве образующей описанного цилиндра (рис. 6, 7, 8).

Видео:Построение врезок двух геометрических фигурСкачать

Цилиндр, конус, шар

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям. Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

Основания цилиндра равны и лежат в параллельных плоскостях.
Все образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его основания ($R$).
Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.

Читайте также: Какое давление должно быть в цилиндре скутера

Площадь поверхности и объем цилиндра.

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.

Объем цилиндра равен произведению площади основания на высоту.

Объем части цилиндра, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.

Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.

Распишем формулы объема цилиндра и шара.

Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.

Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.

Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.

Все образующие конуса равны.
Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.

Площадь поверхности и объем конуса.

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.

Объем конуса равен трети произведения площади основания на высоту.

Объем части конуса, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).

Тело, ограниченное сферой, называется шаром.

Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.

Площадь поверхности сферы: $S_ =4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы

Объем шара: $V= / = / $, где $R$ — радиус шара, $d$ — диаметр шара.

Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Читайте также: Производство цилиндров глубокой печати

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$ / $	$ / $	$ / $
$cosα$	$ / $	$ / $	$ / $
$tgα$	$ / $	$1$	$√3$
$ctgα$	$√3$	$1$	$ / $

Признаки подобия треугольников:

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Видео:ТЕМА 4. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА: ШАР, КУБ, ЦИЛИНДРСкачать

Ghenadie Sontu Fine Art

Видео:Видеоурок по математике "Цилиндр"Скачать

BLOG

Видео:врезка куб и цилиндр - Костромина Татьяна АлександровнаСкачать

Как рисовать цилиндр? Подробная инструкция рисования цилиндра.

Цилиндр — геометрическое тело, форма которого состоит из трех поверхностей: двух одинаковых по форме плоских кругов и одной, образующей форму, цилиндрической поверхности. Для того чтобы лучше разобраться и понять конструктивную основу строения формы цилиндра, в качестве наглядного пособия рассмотрим его каркасную модель. Изготовить такую модель-каркас не составляет труда. Для этого можно использовать проволоку — алюминиевую, медную, стальную или из мягкого сплава. Длина большой стороны каркаса может быть в пределах 7-10 см.

Изучение в рисунке каркасных моделей позволяет студентам лучше освоить конструктивную сущность предмета, его взаимосвязь и пространственность формы.

Рис.49. Перспективное построение окружностей оснований цилиндра: а — с одной точкой схода; б — с двумя точками схода

Изображение геометрического тела, расположенного на горизонтальной плоскости в обычном вертикальном положении, следует начинать с построения его основания. Как видно, на основаниях цилиндра имеются круглые по форме поверхности, ограниченные окружностью. С окружностью мы уже ознакомились и знаем методы и способы ее построения на плоскости. Основываясь на методе линейно-конструктивного построения изображения каркасных моделей, следует перейти к рассмотрению изображения цилиндра.

Изображение цилиндра следует начинать с определения основных пропорциональных величин — диаметра оснований и высоты.

Построение плоскостей кругов оснований производят тем же способом, что и при изображении окружностей — вписыванием в квадрат (рис.48).

Ось вращения тела (ось цилиндра) всегда перпендикулярна к плоскостям кругов основания. При прорисовывании окружности в квадратах их вертикальные и горизонтальные оси попадают своими концами в середины сторон квадрата, т.е. в точки касания окружности со сторонами поверхности цилиндра (рис.48,49).

Рассматривая форму каркаса цилиндра, видим, что нижнее основание шире верхнего, следовательно, ближняя высота поверхности цилиндра больше, чем дальняя. Их различия обусловлены перспективной закономерностью. При этом необходимо заметить, что чрезмерно широкое нижнее основание цилиндра не способствует правильному и убедительному построению рисунка цилиндра. Поэтому ширина нижнего эллипса относительно верхнего должна быть чуть больше, равно как при наблюдении цилиндра с дальней точки зрения, а не с ближней.

При изображении окружностей оснований эллипса на гипсовом цилиндре его нижнее основание следует прорисовывать насквозь, т.е. видимым, с последующим его удалением для продолжения работы с помощью светотеней. Это даст возможность проследить за различиями в размерах оснований.

Завершив перспективное построение окружностей оснований цилиндра, приступайте к прорисовке краев формы образующей поверхности, соединяющей оба круга. При этом линии не должны быть чрезмерно контрастными, так как они находятся дальше, чем ближние поверхности цилиндра — ближние края эллипса и его изображающая поверхность. Однако без усиления линий ближних краев оснований получить в рисунке достаточное впечатление объемно-пространственной формы невозможно.

По окончании работы над построением рисунка цилиндра необходимо приступить к его проверке. Проверять следует, отходя от своего места на расстояние не менее 2-4 м, в зависимости от размера рисунка. Чем больше его размер, тем с большего расстояния его следует рассматривать.

Внимательно проверив допущенные в процессе работы ошибки, их следует, не откладывая, исправить.

Изображение цилиндра в горизонтальном положении имеет свои особенности в отличие от построения цилиндра в вертикальном положении. Это обусловлено его цилиндрической образующей поверхностью, связывающей между собой оба круглых основания цилиндра. Для примера рассмотрим каркас цилиндра (рис.52).

Цилиндр в горизонтальном положении можно строить на основе прямоугольной призмы. Это облегчает объемно-пространственное и конструктивное построение цилиндра, позволяет правильно определить ось вращения по отношению к оси эллипса и, следовательно, правильно строить окружности оснований (эллипсы). Определив линию горизонта и положение предмета в пространстве относительно угла зрения (в этом случае цилиндр находится несколько сбоку, а точка зрения выше цилиндра), нужно наметить его местоположение. При построении очень важно правильно определить углы горизонтальных направлений предмета на плоскости, поэтому изображение призмы начинают с построения ее основания, у которого все стороны попарно равны высоте цилиндра и диаметру оснований окружностей. В последующем эта призма будет служить каркасом для построения цилиндра в горизонтальном положении.

Построение призмы производят с ближайших к нам точек на пересечении сторон параллелепипеда. В соответствии с положением предмета нужно наметить горизонтальную, уходящую по направлению к точкам схода линию основания сторон призмы. Направления этих двух основных линий, идущих к точкам схода, должны определять основу для правильного построения призмы, а затем — цилиндра. После чего производят построение с учетом перспективы. Для определения точек осевой линии призмы следует провести диагонали противоположных углов ее передней грани. Точка пересечения диагоналей будет центром оси призмы и цилиндра. Чтобы правильно вписать окружность основания цилиндра (эллипс) в переднюю грань призмы, необходимо точно определить прямой угол между осью призмы и отрезком линии, которая и будет большой осью эллипса. Эта важная деталь, о ней следует всегда помнить студентам, является причиной грубых ошибок при изображении цилиндра в горизонтальном положении. При этом, независимо от ракурсов и углов поворота, прямой угол между большой осью эллипса и осью вращения тела является основой для правильного построения окружностей оснований в его горизонтальном положении.

Итак, определив прямой угол, приступайте к вписыванию окружностей оснований цилиндра. Здесь большая ось будет определять наибольший диаметр основания, а малая, которая располагается по оси цилиндра, — наименьший.

Следует обратить внимание, что дальнее основание цилиндра по мере удаления от рисующего всегда несколько шире (по малой оси), чем переднее. Это обусловлено закономерностью перспективы.

Построив таким образом основания и дополнительно уточнив окружности (эллипсы), соединяют их образующими. В завершающей стадии построения изображения следует придать рисунку большую пространственность за счет усиления линий близлежащих и ослабления линий дальних форм.

Завершив построение, следует непременно его проверить. Внимательно проверив возможные ошибки, допущенные в процессе построения, и исправив их (если таковые имеются), следует перейти к длительному рисунку с помощью света, тени, полутени и рефлекса.

Для продолжения работы над длительным рисунком студентам необходимо дополнительное изучение закономерностей распределения светотеней. Без этого невозможно переходить к практическому выполнению учебных задач в академическом учебном рисунке. Вопросы, касающиеся законов света и теней, изложены в конце этого раздела.