Как вписать тетраэдр в цилиндр (5 видео)

Содержание

Пирамида, вписанная в цилиндр. Свойства пирамиды, вписанной в цилиндр
Отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды
ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР И ИХ КОМБИНАЦИЙ
Дистанционное обучение как современный формат преподавания
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
📹 Видео

Видео:Видеоурок по математике "Цилиндр"Скачать

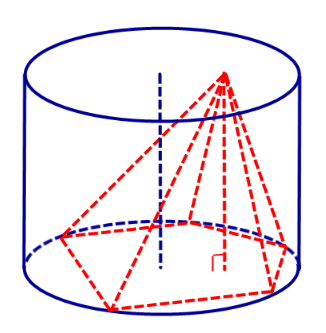
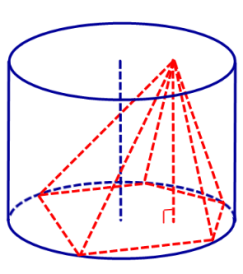
Пирамида, вписанная в цилиндр. Свойства пирамиды, вписанной в цилиндр

Определение 1. Пирамидой, вписанной в цилиндр, называют такую пирамиду, у которой основание вписано в одно из оснований цилиндра, а вершина лежит на другом основании цилиндра (рис. 1).

Определение 2. Если пирамида вписана в цилиндр, то цилиндр называют описанным около пирамиды.

Замечание. Если пирамида вписана в цилиндр, то высота пирамиды равна высоте цилиндра.

Из определения пирамиды, вписанной в цилиндр, легко вытекает следующее утверждение, доказательство которого мы оставляем читателю.

Утверждение. Около любой правильной пирамиды можно описать цилиндр.

Видео:Математика ЕГЭ. В цилиндр вписан правильный тетраэдрСкачать

Отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды

Задача. Найти отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды.

Решение. Поскольку объем цилиндра вычисляется по формуле

а объем пирамиды вычисляется по формуле

Поскольку площадь правильного n — угольника выражается через радиус R описанной около этого многоугольника окружности по формуле

Следствие 1. Отношение объема правильной треугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 2. Отношение объема правильного тетраэдра к объему цилиндра, описанного около данного тетраэдра, равно

Следствие 3. Отношение объема правильной четырехугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 4. Отношение объема правильной шестиугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Видео:10 класс, 12 урок, ТетраэдрСкачать

ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР И ИХ КОМБИНАЦИЙ

Ищем педагогов в команду «Инфоурок»

ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР

Задание: построить изображение правильной треугольной пирамиды, вписанной в сферу (Рис. 1).

Прежде всего, отметим, что изображение шара выполняем в ортогональной проекции, а, следовательно, построения изображений комбинаций шара с другими фигурами также выполняется в ортогональной проекции.

Порядок построения изображений следующий:

Строим изображения очерка сферы и ее полюсов.

Строим изображение параллели.

Строим изображение правильного треугольника, вписанного в параллель.

Вершина пирамиды совпадает с полюсом N .

Задание: построить изображение куба, вписанного в сферу (Рис. 2).

Строим изображение сферы и ее полюсов.

Читайте также: Если нет компрессии в цилиндрах клапана целые

Строим изображение параллелей. Выразим длину ребра куба через радиус сферы. Пусть R – радиус сферы, a – длина ребра куба. 4 R 2 = a 2 + 2 a 2 a = . Следовательно, параллели отстоят от экваториальной плоскости на расстоянии ОО ₁ = ОО ₂ = , т.е. ОО ₂ :О S = 1: .

Строим изображение квадрата, вписанного в окружность, — нижний эллипс с центром О ₂ .

Построение изображения правильной n -угольной призмы, вписанной в сферу, выполняется аналогично.

Задание: Построить изображение цилиндра, вписанного в сферу (Рис. 3).

Основания цилиндра – параллели, плоскости которых расположены на одинаковом расстоянии от центра.

Ось цилиндра лежит на оси сферы.

Задание: Построить изображение конуса, вписанного в сферу (Рис. 4).

Строим изображение сферы и ее полюсов.

Основание конуса – любая параллель.

Ось конуса лежит на оси сферы, полюс N является вершиной конуса.

Задание: Построить изображение цилиндра, описанного около сферы (Рис. 5).

Строим изображение сферы и ее полюсов, экватор с диаметром АВ .

Экватор является пересечением сферы и боковой поверхности цилиндра, полюсы являются точками касания сферы и оснований цилиндра.

Через точки А, В, N и S проведем попарно перпендикулярные отрезки. Получим квадрат CDFE .

Строим изображение верхнего и нижнего оснований цилиндра — эллипсы с большими осями EF = CD = AB , а меньшие ос равны меньшей оси экваториального эллипса.

DF и CE – образующие цилиндра, NS – его ось, совпадающая с осью сферы.

Задание: Построить изображение правильной треугольной призмы, описанной около сферы (Рис. 6).

Строим изображение правильного треугольника АВС , описанного около экватора.

Через вершины треугольника АВС проводим прямые, параллельные NS , и на них откладываем отрезки, равные ON , по обе стороны от плоскости экватора.

Строим изображение призмы.

Задание: Построить изображение шара, вписанного в правильный тетраэдр (Рис. 7).

Строим изображение правильного тетраэдра SABC .

Центр сферы принадлежит высоте SO пирамиды и биссектрисе линейного угла при основании, лежащей в плоскости, которая проходит через высоту пирамиды. Точка О – точка касания шара с основанием АВС .

Треугольник SKA – равнобедренный, МК – биссектриса и высота, отсюда О ₁ = SOKM , О ₁ – центр шара. Так как все грани правильного тетраэдра равноправны, то точки касания шара с другими боковыми гранями есть их центроиды.

Задание: Построить изображение вписанной в цилиндр правильной шестиугольной призмы (Рис. 8).

Замечание: Изображение многогранников, вписанных в цилиндр, конус или описанных около них, практически сводится к изображению оснований этих многогранников, вписанных в окружности оснований цилиндра и конуса или описанных около них. Этот вопрос подробно освещен выше, поэтому ограничимся двумя изображениями (Рис. 8, 9).