Как вписать цилиндр в сферу (5 видео)

Содержание

Касательная прямая к сфере. Касательная плоскость к сфере
Сфера, вписанная в цилиндр
Отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар
Нахождение радиуса/площади/объема описанной вокруг цилиндра сферы (шара)
Нахождение радиуса сферы/шара
Вписанные и описанные цилиндры.
Просмотр содержимого документа «Вписанные и описанные цилиндры.»
🎥 Видео

Видео:Видеоурок по математике "Цилиндр"Скачать

Касательная прямая к сфере. Касательная плоскость к сфере

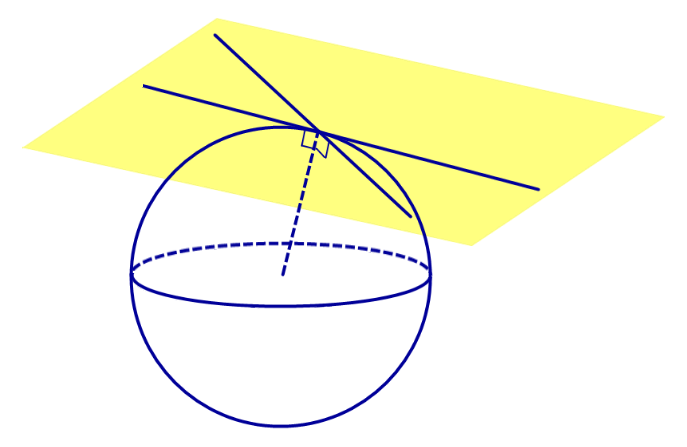
Определение 1. Прямую называют касательной к сфере (прямой, касающейся сферы), если эта прямая имеет со сферой единственную общую точку. Общую точку касательной прямой и сферы называют точкой касания (рис. 1).

Прямая касается сферы тогда и только тогда, когда эта прямая проходит через точку касания и перпендикулярна радиусу сферы, проведенному в точку касания.

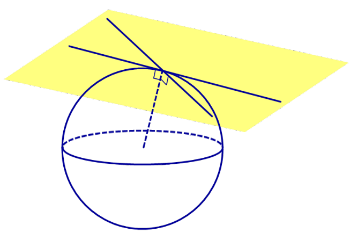
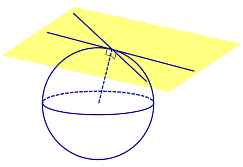
Множество всех прямых, касающихся сферы в некоторой точке, образуют касательную плоскость к сфере в этой точке (рис.2).

Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем только одну.

Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем плоскость перпендикулярна радиусу сферы, проведенному в эту точку.

Общую точку сферы и ее касательной плоскости называют точкой касания .

Видео:Цилиндр, конус, шар, 6 классСкачать

Сфера, вписанная в цилиндр

Определение 2. Сферой, вписанной в цилиндр, называют такую сферу, которая касается плоскостей обоих оснований цилиндра, а каждая образующая цилиндра является касательной к сфере (рис. 3).

Определение 3. Если сфера вписана в цилиндр, то цилиндр называют описанным около сферы .

Из рисунка 3 видно, что справедливы следующие два утверждения.

Утверждение 1. Около любой сферы можно описать цилиндр.

Утверждение 2. В цилиндр можно вписать сферу тогда и только тогда, когда высота цилиндра равна диаметру его основания.

Замечание. В том случае, когда в цилиндр можно вписать сферу, радиус вписанной сферы равняется радиусу основания цилиндра.

Видео:ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

Отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар

Задача. Найти отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар.

Читайте также: Для чего применяется цилиндр в химии

Видео:Пересечение поверхностей полусферы и цилиндра. Пошаговое видео. Инженерная графикаСкачать

Нахождение радиуса/площади/объема описанной вокруг цилиндра сферы (шара)

В данной публикации мы рассмотрим, как найти радиус описанной вокруг прямого цилиндра сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.

Видео:ЦИЛИНДР // КОНУС // ШАРСкачать

Нахождение радиуса сферы/шара

Около любого цилиндра можно описать сферу (или другими словами, вписать цилиндр в шар) – но только одну.

Можно заметить, что радиус описанной сферы (OE), половина высоты цилиндра (OO₁) и радиус его основания (O₁E) образовывают прямоугольный треугольник OO₁E.

Воспользовавшись теоремой Пифагора мы можем найти гипотенузу этого треугольника, которая одновременно является радиусом сферы, описанной около заданного цилиндра:

Зная радиус сферы можно вычислить площадь (S) ее поверхности и объем (V) ограниченного сферой шара:

Примечание: π округленно равняется 3,14.

Видео:11 класс, 19 урок, Сфера и шарСкачать

Вписанные и описанные цилиндры.

Презентация для учащихся 11 класса по теме «Комбинация тел» содержит краткую теорию и примеры решения задач на комбинации цилиндра и щара, цилиндра и призмы.Будет полезна при подготовке к ЕГЭ.

Просмотр содержимого документа
«Вписанные и описанные цилиндры.»

Сфера, вписанная в цилиндр

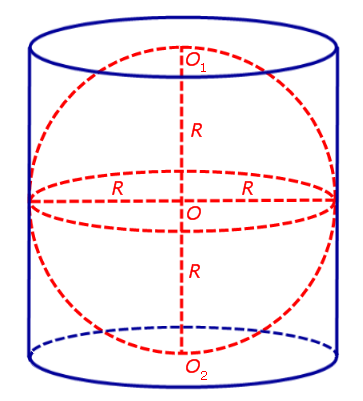
Сфера называется вписанной в цилиндр, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом цилиндр называется описанным около сферы.

В цилиндр можно вписать сферу, если высота цилиндра равна

Ее центром будет точка O , являющаяся

серединой отрезка, соединяющего центры оснований O 1 и O 2 цилиндра.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Радиус сферы R будет равен

радиусу окружности основания цилиндра.

В цилиндр высоты 2 вписана сфера. Найдите ее радиус.

В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра.

Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра, чтобы в него можно было вписать сферу?

Высота цилиндра равна 2. Каким должен быть радиус основания цилиндра, чтобы в него можно было вписать сферу?

Осевым сечением цилиндра является прямоугольник со сторонами 1 и 2. Можно ли в этот цилиндр вписать сферу?

Читайте также: Полировка цилиндров двигателя в зеркало

Осевым сечением цилиндра является квадрат. Можно ли в этот цилиндр вписать сферу?

Можно ли вписать сферу в цилиндр, осевым сечением которого является ромб?

Можно ли вписать сферу в наклонный цилиндр?

Площадь осевого сечения цилиндра, в который вписана сфера, равна 4 см 2 . Найдите диаметр сферы.

Периметр осевого сечения цилиндра, в который вписана сфера, равен 8 см. Найдите радиус сферы.

Какой наибольший радиус может быть у сферы, помещающейся в цилиндр, радиус основания которого равен 2, и высота 1.

Можно ли сферу радиуса 1 поместить в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60 о .

Какой наибольший радиус может быть у сферы, помещающейся в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60 о .

Сфера, описанная около цилиндра

Цилиндр называется вписанным в сферу, если окружности оснований цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра.

Около любого цилиндра можно описать сферу. Ее центром будет точка O , являющаяся серединой отрезка, соединяющего центры оснований O 1 и O 2 цилиндра.

Радиус сферы R вычисляется по формуле

где h – высота цилиндра, r – радиус окружности основания.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Диагональ осевого сечения цилиндра равна 2. Найдите радиус сферы, описанной около этого цилиндра.

Около цилиндра высоты 2 и радиуса основания 1 описана сфера. Найдите ее радиус.

Около цилиндра, радиус основания которого равен 1, описана сфера радиуса 2. Найдите высоту цилиндра.

Около цилиндра, высота которого равна 1, описана сфера радиуса 1. Найдите радиус основания цилиндра.

Найдите наименьший радиус сферы, в которую помещается наклонный цилиндр, радиус основания которого равен 1, образующая равна 2 и наклонена к плоскости основания под углом 60 о .

Цилиндр, вписанный в призму

Ц илиндр называется вписанным в призму, если е го основания в писаны в основани я цилиндра. При этом , призма называется описанной около цилиндра

Читайте также: Цилиндр в машине прокладка

В призму можно вписать цилиндр тогда и только тогда, когда

в ее основание можно вписать окружность.

Радиус основания цилиндра равен

радиусу окружности, вписанной в основание призмы.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Можно ли вписать цилиндр в наклонную призму?

Ответ: Да, наклонный цилиндр.

В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, вписанного в эту призму.

В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, вписанного в эту призму.

Найдите радиус окружности основания цилиндра, вписанного в единичный куб.

В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр. Найдите радиус окружности основания этого цилиндра.

Цилиндр, описанный около призмы

Ц илиндр называется описанным около призмы, если е го основания о писаны около основани й цилиндра. При этом , п ризма называется вписанной в цилиндр

Около призмы можно описать цилиндр, если около ее оснований можно описать окружности.

Радиус основания цилиндра равен

радиусу окружности, описанной около основания призмы.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Можно ли описать цилиндр около наклонной призмы?

Ответ: Да, наклонный цилиндр.

В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.

В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, описанного около этой призмы.

В основании прямой призмы квадрат со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.

Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр. Найдите радиус окружности основания этого цилиндра.

Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат окружностям оснований цилиндра. Найдите радиус основания и высоту цилиндра.

Около единичного октаэдра описан цилиндр так, что две противоположные вершины октаэдра находятся в центрах оснований цилиндра, а остальные вершины принадлежат боковой поверхности цилиндра. Найдите радиус основания и высоту цилиндра.