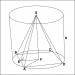
Как врезать цилиндр в пирамиду (6 видео)

Пересечение прямого кругового цилиндра с поверхностью пирамиды.

На рис 17 показано пересечение цилиндра и правильной шестиугольной пирамиды. Сначала определяется на каких проекциях нужно строить линию пересечения. Затем определяют характерные точки. Дополнительные точки строятся с помощью вспомогательных горизонтальных плоскостей.

Раздел 5 Взаимное пересечение поверхностей двух тел вращения.

5.1 Пересечение поверхностей цилиндров.

Построение линии пересечения цилиндров начинают со сравнения их оснований. На рис. 18 изображены три вертикальных цилиндра (А,Б,В) разных диаметров, которые пересекаются с половиной горизонтального цилиндра.

Рассмотрим, какая получается линия пересечения в зависимости от соотношения диаметров цилиндров. Если пересекаются два цилиндра разных диаметров, то линия их пересечения представляет собой кривую, кривизна которой зависит от разности диаметров. Чем больше разность, тем меньше кривизна, и наоборот. При этом изгиб кривой всегда идет в сторону большего диаметра, так как цилиндр с меньшим диаметром как бы проходит через цилиндр с большим диаметром. Если же диаметры одинаковые, то линия пересечения изображается прямыми линиями, имея форму эллипсов.

5.2 Построение пересечения поверхностей тел вращения с помощью вспомогательных секущих плоскостей.

Линии пересечения тел вращения обычно строят с помощью вспомогательных секущих плоскостей Р (рис. 19). Каждая плоскость пересекает одновременно оба тела вращения по соответствующим линиям. Эти линии пересекаются между собой в точках, определяющих линию пересечения заданных поверхностей. Количество вспомогательных плоскостей берется в зависимости от требуемой точности построения.

Еще один пример на рис. 20. Здесь рассматривается построение линии пересечения конуса и шара. Вспомогательные плоскости — фронтально-прецирующие плоскости N, R, Т, М.

Содержание

Вписанный в пирамиду цилиндр. Цилиндр и пирамида: варианты комбинаций
Пирамида в геометрии
Цилиндр в геометрии
Многоугольник и окружность
Треугольная пирамида, вписанная в цилиндр
Пирамида четырехугольная, вписанная в цилиндр
Цилиндр вписан в фигуру
Задача с четырехугольной пирамидой и цилиндром
Врезка куба и цилиндра
Врезка пирамиды и цилиндра
📺 Видео

Видео:Сложные врезки Цилиндр и пирамидаСкачать

Вписанный в пирамиду цилиндр. Цилиндр и пирамида: варианты комбинаций

Одними из интересных задач, которые позволяют сравнить различные объемные фигуры, являются задачи на описание одной из них около другой. В данной статье рассмотрим различные варианты описанного около пирамиды и вписанного в пирамиду цилиндра.

Видео:Построение врезок двух геометрических фигурСкачать

Пирамида в геометрии

Прежде чем изучать комбинации вписанного в пирамиду цилиндра и вписанной пирамиды в цилиндр, следует рассмотреть эти фигуры с точки зрения геометрии. Начнем с пирамиды.

Фигура пирамида представляет собой тело в пространстве, которое получается, если соединить все вершины произвольного плоского n-угольника с некоторой точкой в пространстве. При этом n-угольник может быть совершенно произвольным (выпуклым, вогнутым, правильным, с различным количеством сторон n). На положение отмеченной точки накладывается одно единственное условие: она не должна лежать в той плоскости, в которой n-угольник находится.

На рисунке выше показана, пожалуй, самая известная пирамида — четырехугольная. Видно, что вершины четырехугольника, который называется основанием фигуры, соединены с точкой, лежащей над ним. Эта точка называется вершиной пирамиды.

Приведенное определение и также представленный рисунок свидетельствуют, что любая пирамида, независимо от типа ее основания, будет включать в себя n треугольников. Все они соединяются в вершине фигуры.

Перпендикулярный отрезок, проведенный из вершины фигуры к ее основанию, называется высотой. Если высота пересекает в геометрическом центре n-угольник, то такая пирамида будет прямой. В противном случае имеет место наклонная фигура.

Читайте также: Замена главного цилиндра сцепления бмв е36

Если все стороны n-угольника равны между собой, и фигура является прямой, то ее называют правильной. Именно с правильными пирамидами удобно работать при изучении их взаимного расположения с другими объемными телами в геометрии.

Видео:врезка куб и пирамида - Костромина Татьяна АлександровнаСкачать

Цилиндр в геометрии

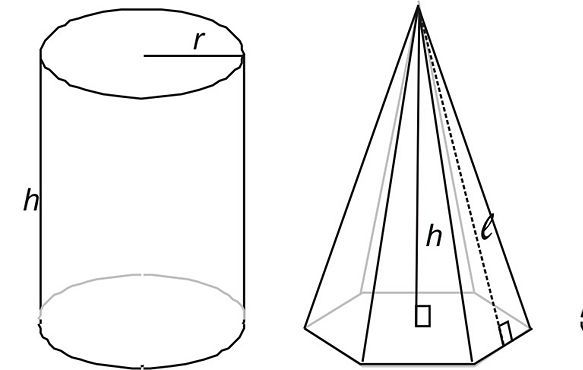
Цилиндр в общем случае можно получить, если вдоль замкнутой кривой перемещать отрезок параллельно самому себе таким образом, чтобы отрезок не лежал в плоскости этой кривой. Этот отрезок называется образующей цилиндра, а кривая, вдоль которой он перемещается, носит название направляющей.

Если направляющая является окружностью, а образующая ей перпендикулярна, то полученный цилиндр будет называться прямым с круглым основанием. Эта фигура известна каждому. Она представлена на рисунке ниже.

Далее будем рассматривать только прямой круглый цилиндр.

В отличие от пирамиды, цилиндр не имеет вершин и ребер. Однако он образован двумя основаниями (два одинаковых круга, находящихся в параллельных плоскостях) и боковой цилиндрической поверхностью. Если посмотреть на развертку этой фигуры, то можно увидеть, что она состоит из двух кругов и одного прямоугольника (см. рис. ниже).

Основными характеристиками цилиндра являются следующие:

радиус основания;
высота — расстояние между основаниями;
площадь оснований и боковой поверхности;
объем фигуры.

Видео:Как сделать объемный ЦИЛИНДР из бумаги? ||| Геометрические фигуры своими рукамиСкачать

Многоугольник и окружность

Последний вопрос, который следует изучить перед тем, как рассматривать вписанный в пирамиду цилиндр и описанный около нее, связан с взаимным расположением правильного многоугольника и окружности.

Существуют всего два варианта расположения этих плоских фигур:

описание окружностью n-угольника;
описание n-угольником окружности.

Приведем формулы, позволяющие вычислить длину стороны многоугольника через радиус окружности. Рассмотрим для примера только два первых многоугольника, то есть равносторонний треугольник и квадрат.

Если окружность проходит через все вершины n-угольника, то говорят, что она его описывает. При известном радиусе R длина стороны вычисляется по формуле:

То есть сторона квадрата, вписанного в окружность с радиусом R, будет немного меньше таковой для равностороннего треугольника, описанного той же окружностью.

Если окружность касается каждой из сторон n-угольника, то говорят, что она вписана в него. В случае правильных многоугольников точка касания фигур находится точно посередине каждой стороны n-угольника. Если известен радиус r окружности вписанной, тогда сторона n-угольника определится по формуле:

То есть вокруг окружности фиксированного радиуса можно описать треугольник с большей длиной стороны, чем квадрат.

Видео:ТЕМА 4. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА: ШАР, КУБ, ЦИЛИНДРСкачать

Треугольная пирамида, вписанная в цилиндр

Сначала рассмотрим более простой вариант, то есть когда пирамида находится внутри цилиндра. Разберем конкретный пример с правильной треугольной пирамидой. Предположим, что известен радиус R цилиндра и его высота h. Необходимо найти характеристики правильной треугольной пирамиды, вписанной в цилиндр.

Выше уже была приведена формула для стороны равностороннего треугольника, находящегося внутри окружности. Длина его стороны является длиной основания пирамиды. Она равна:

Вершина пирамиды вписанной лежит точно в центре верхнего основания цилиндра, поэтому высоты обеих фигур равны.

Зная длину стороны основания и высоту правильной пирамиды треугольной, можно рассчитать другие ее характеристики. Например, объем вычисляется по формуле:

Длину бокового ребра a_b можно рассчитать так:

Видео:ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Пирамида четырехугольная, вписанная в цилиндр

Как и в предыдущем случае, пирамида находится внутри цилиндра. Только теперь ее основание представляет собой квадрат, сторона которого через радиус R цилиндра вычисляется так:

Высота пирамиды равна таковой для цилиндра, то есть h.

Длина бокового ребра a_b составляет:

Заметим, что формула для длины бокового ребра получилась точно такой же, как в случае треугольной пирамиды.

Читайте также: Как самому заменить тормозные цилиндры

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Цилиндр вписан в фигуру

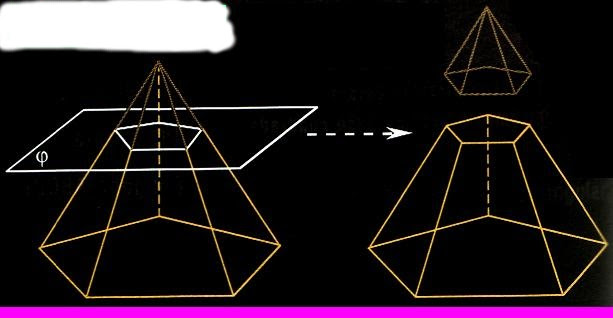
Цилиндр, вписанный в пирамиду, представляет более сложный случай расположения этих фигур. Чтобы рассчитать размеры пирамиды по известному радиусу и высоте цилиндра, следует разобраться, как этот цилиндр будет расположен внутри нее.

Предположим, что имеется плоскость, параллельная основанию пирамиды. Пересечем этой плоскостью боковую поверхность фигуры. Образованное сечение будет представлять точно такой же многоугольник, что лежит в основании, но меньшего размера. Этот многоугольник будет описывать верхнее основание цилиндра. Нижнее основание будет лежать в основании пирамиды.

Чтобы найти длину стороны многоугольника сечения, следует воспользоваться функцией зависимости площади сечения от вертикальной координаты z. Эта функция имеет вид:

Здесь z — расстояние от основания пирамиды вдоль ее высоты, h_p — высота пирамиды.

Как пользоваться этой формулой для определения параметров описанной около цилиндра пирамиды, покажем на примере решения задачи.

Видео:ВРЕЗКА ФИГУР. СФЕРА и ПИРАМИДАСкачать

Задача с четырехугольной пирамидой и цилиндром

Известно, что цилиндр имеет радиус r = 5 см и высоту h = 6 см. Найти высоту и сторону правильной четырехугольной пирамиды, описывающей его.

Верхнее основание цилиндра должно вписываться в квадратный срез на высоте h = 6 см от основания пирамиды. Тогда площадь сечения равна:

Здесь a — сторона основания пирамиды. Если взять квадратный корень из S(6), то получим длину стороны квадрата сечения. Она должна быть равна 2*r, чтобы основание цилиндра могло вписаться в это сечение, тогда получаем:

Отсюда получаем выражение:

Таким образом, вписать цилиндр, заданный условием задачи, можно не в одну единственную правильную четырехугольную пирамиду, а в бесконечное их число. Однако параметры каждой из них должны удовлетворять выражению выше, которое связывает высоту фигуры с длиной стороны ее основания.

Видео:Пересечение многогранников. Пирамида с призматическим вырезом.Скачать

Врезка куба и цилиндра

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку куба и цилиндра. Оценить многообразие возможных связок куба и цилиндра, отработать приемы построения их врезок, научиться создавать на листе связки с гармоничными пропорциями.

ПОСТАНОВКА ЗАДАНИЯ. Нарисуйте связки куба и цилиндра сначала по заданным ортогональным проекциям, а затем в произвольном положении по отношению друг к другу. Найдите наиболее красивые, гармоничные пропорции связок, изменяя положение линии пересечения геометрических тел.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Рассмотрите ортогональные проекции двух геометрических тел — куба и цилиндра — на рис. 5.46. Представьте взаимное положение тел. Изобразите в перспективе заданную связку куба и цилиндра с различным положением относительно линии горизонта (выше линии горизонта на рис. 5.47 и ниже линии горизонта на рис. 5.48).

Изобразите куб и вертикальный цилиндр в положении, представленном на рис. 5.49. Предложите несколько вариантов врезок, например, как на рис. 5.50 и 5.51. Тонируйте любую связку (рис. 5.52).

Изобразите куб и горизонтальный цилиндр (рис. 5.53). Предложите гармоничные врезки, например, как на рис. 5.54 и 5.55 (тон на рис. 5.56).
Теперь попробуйте сделать подобное упражнение, увеличив количество геометрических тел. Связка тел — куба и трех цилиндров — предлагается на рис. 5.57. Постройте врезки, например, как это сделано на рис. 5.58. Легко тонируйте композицию (рис. 5.59).

Видео:ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

Врезка пирамиды и цилиндра

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку тела вращения и тела с наклонными гранями.

ПОСТАНОВКА ЗАДАНИЯ. Постройте врезку пирамиды и цилиндра.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Изобразите пирамиду и цилиндр (рис. 5.152). Представьте линию врезки. Наклонные грани пирамиды рассекают цилиндр по эллипсам. Сечение цилиндра основанием пирамиды — окружность. Сечение пирамиды верхним основанием цилиндра — квадрат, подобный квадрату основания пирамиды. Из всех этих сечений, пожалуй, наиболее сложные — сечения цилиндра наклонными плоскостями.
Для построения таких сечений необходимы две вспомогательные вертикальные секущие плоскости, проходящие через ось цилиндра. Эти плоскости перпендикулярны друг другу и наклонным граням пирамиды (рис. 5.153 и 5.154).

Читайте также: Задний тормозной цилиндр сузуки гранд витара 2008

Постройте сначала линию пересечения цилиндра и наклонной грани пирамиды, выделенной на рис. 5.155.

Найдите такое ее положение, которое даст гармоничные соотношения поверхностей геометрических тел. Зафиксируйте нижнюю точку секущего эллипса — точку А на пересечении вертикальной вспомогательной плоскости и наклонной грани пирамиды (рис. 5.156), постройте сечение (рис. 5.157).

После построения первой линии сечения взаимное положение геометрических тел стало определенным, что дает возможность построить остальные
линии сечения.
Вариантов дальнейшего построения может быть несколько. Например, если достроить сечение пирамиды вспомогательной плоскостью, которую мы уже использовали в построении наклонного сечения, то можно получить несколько опорных точек (рис. 5.158). Точки В и С определяют положение линии сечения пирамиды верхним основанием цилиндра, точка О — центр окружности сечения цилиндра горизонтальной плоскостью основания пирамиды, а точки D и Е — раскрытие эллипса этого сечения на вашем рисунке.

Постройте горизонтальное сечение цилиндра (рис. 5.159), а затем по опорным точкам на пересечении пирамиды и второй вспомогательной секущей плоскости (рис. 5.160) постройте сечение цилиндра второй наклонной гранью пирамиды (рис. 5.161). В этом задании мы ограничимся построением только видимых линий сечения. Однако, при необходимости, вы можете построить все линии. Затем усильте основные линии рисунка (рис. 5.162) и тонируйте связку (рис. 5.163).

Можно предложить и другую последовательность построения. Она уместна тогда, когда положение геометрических тел заранее определено, например, в ортогональных проекциях (рис. 5.164). В этом случае лучше начать построение с вертикального цилиндра. Задайте перспективные направления при помощи двух вертикальных секущих плоскостей (рис. 5.165) — эти плоскости впоследствии пригодятся нам в построении наклонных сечений.
Чтобы изобразить пирамиду, определите, где плоскость ее основания пересекает вертикальную ось цилиндра, и постройте секущий эллипс (рис. 5.166).

Определите положение точки центра основания пирамиды относительно центра окружности сечения (рис. 5.167), для чего сначала опишите вокруг секущего эллипса квадрат. Центр основания пирамиды смещен относительно центра окружности сечения по диагонали этого квадрата примерно на треть радиуса (это следует из плана). Нарисуйте квадрат основания пирамиды. Из точки пересечения диагоналей квадрата поднимите вертикаль, отложите на ней высоту пирамиды и достройте наклонные ребра (рис. 5.168). Таким образом мы получили связку с точным положением геометрических тел в пространстве.

Теперь достройте линию сечения. Чтобы построить сечение цилиндра наклонными гранями пирамиды, воспользуйтесь вспомогательными вертикальными секущими плоскостями, проходящими через вертикальную ось цилиндра (мы изобразили их в самом начале построения). Выберите любую вспомогательную плоскость. Линия сечения этой плоскостью цилиндра — вертикальный прямоугольник. Линия сечения пирамиды этой же вспомогательной плоскостью — трапеция. На рис. 5.169 прямоугольник и трапеция графически выделены тоном и толстой линией. На пересечении прямоугольника и трапеции получите опорные точки, необходимые для дальнейшего построения. Изобразите наклонное сечение цилиндра. Затем проделайте эти же действия с другой вспомогательной секущей плоскостью (рис. 5.170).