Как вычислить площадь цилиндра см2

Используя этот онлайн калькулятор, вы сможете найти площадь боковой поверхности цилиндра, а также площадь полной поверхности цилиндра.

Воспользовавшись онлайн калькулятором для вычисления площади поверхности цилиндра, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

Видео:Видеоурок по математике "Цилиндр"Скачать

Найти площадь поверхности цилиндра

Введите значение радиуса цилиндра и его высоты

Ввод данных в калькулятор для вычисления площади цилиндра

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!

Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.

Дополнительные возможности калькулятора вычисления площади цилиндра

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Теория. Площадь поверхности цилиндра

— геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями (основаниями), пересекающими её.

Цилиндр называется круговым, если его основание – круг. Расстояние между основаниями – высота цилиндра.

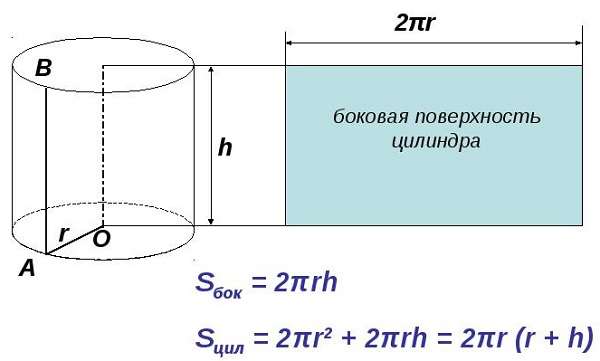
Формулы для вычисления площади боковой поверхности цилиндра

Формулы для вычисления площади полной поверхности цилиндра

S = 2 π R h + 2 π R 2 = 2 π R ( R + h )

где S — площадь,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Видео:Цилиндр - расчёт площади, объёма.Скачать

Нахождение площади поверхности цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.

Видео:Объём цилиндраСкачать

Формула вычисления площади цилиндра

1. Боковая поверхность

Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.

Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:

Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:

3. Полная площадь

Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:

S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Читайте также: Компрессия в цилиндрах уаз 469 таблица

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .

Видео:60. Площадь поверхности цилиндраСкачать

Площадь поверхности цилиндра: онлайн-калькулятор

Высчитать площадь полной поверхности цилиндра с помощью нашего сервиса легко. Удобный интерфейс с чертежом иллюстрирует формулу и наглядно показывает, какие данные необходимы для решения задачи.

Все преобразования происходят автоматически и видны в расчетах. Вам остается только ввести известные величины. Сервис работает без регистрации и оплаты. Программа позволяет получить ход вычислений и быстрый ответ, что очень важно на экзаменах, зачетах, контрольных.

1. Введите данные задачи в соответствующие окна.
   
2. Установите нужные единицы измерения. Отправьте задачу на расчет кнопкой «Найти».
   
3. Получите решение и ответ.
   ​​​​​​​

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Нахождение площади поверхности цилиндра. Онлайн-калькулятор

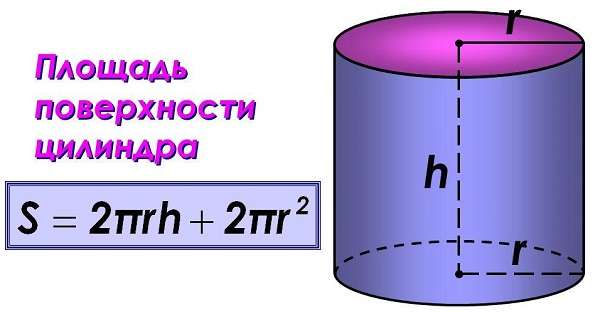
Программа рассчитывает площадь поверхности цилиндра по формуле:

В разделе с калькуляторами собраны расчеты и для других фигур. Для решения составного задания ищите необходимые программы. Вычисления не ограничиваются в количестве. Отсылайте нужное число запросов для усвоения материала. Автоматизированные подсчеты с пошаговыми действиями помогают самостоятельно изучать тему и запоминать алгоритм.

• Школьникам. Самостоятельная подготовка к урокам становится проще и быстрее, когда есть возможность свериться с ответом. Кроме этого родителям больше не понадобится вникать в тему, чтобы проверить подготовку ребенка.
• Студентам. Получить проходной балл можно благодаря автоматизированному подсчету.
• Преподавателям. За счет экономии времени на проверке расчетов можно составить больше индивидуальных заданий и не пересчитывать их вручную.

Если возникли вопросы по теме, обратитесь к консультанту. Наш сотрудник поможет найти преподавателя по вашему запросу. Услуги по объяснению непонятной темы, решению задач и онлайн-помощи стоят недорого.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Площадь цилиндра

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Площадь цилиндра — как правильно рассчитать

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.

Перед тем, как начать вычисление площади цилиндра, необходимо учесть, что существует два ее вида:

1. Полная площадь поверхности цилиндра. Она равна сумме боковой поверхности цилиндра и двойной площади его основания.
2. Площадь боковой поверхности цилиндра. Она равняется произведению высоты цилиндра на длину окружности основания.

Чтобы вычислить общую площадь поверхности цилиндра, нужно применить формулу:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

\(S=2\times\pi\times R\times h+2\times\pi\times R^2=2\times\pi\times R\times\left(h+R\right)\)

Здесь R — радиус окружности, а h — высота.

Чтобы найти площадь боковой поверхности цилиндра, нужно воспользоваться формулой:

Видео:Лучший способ найти площадь кругаСкачать

«Компоненты» стереометрической фигуры

Цилиндр состоит из нескольких составляющих.

1. Цилиндрическая поверхность — это поверхность, которая образуется большим количеством параллельных прямых, проходящих через точки некоторой кривой.
2. Основания — это плоские фигуры, которые образованы пересечением ЦП с двумя параллельными плоскостями, ограничивающими цилиндр. Оснований у цилиндра два.
3. Боковой поверхностью называют часть ЦП, которая находится между основаниями.
4. И, наконец, высота — это отрезок, который высекается плоскостями оснований цилиндра на прямой, перпендикулярной им.

Читайте также: Пропуски зажигания в третьем цилиндре приора

Дополнительно можно измерить периметр S_бок. Для этого нужно длину окружности l сложить с высотой h и умножить данную сумму на 2.

Рассмотрим, как различаются типы рассматриваемой геометрической фигуры по форме. Цилиндр может быть:

1. Прямой. Его основания имеют центры симметрии, то есть являются кругами или эллипсами. При этом прямая между центрами перпендикулярна плоскостям оснований. Данная прямая называется осью цилиндра.
2. Косой. Его основания имеют центры симметрий, однако отрезок между ними не перпендикулярен плоскостям оснований.
3. Круговой. Имеет окружность в роли направляющей.
4. Прямой круговой. Его можно получить с помощью вращения прямоугольника вокруг одной из его сторон. Тогда эта сторона будет осью цилиндра и осью симметрии.
5. Равносторонний. Его диаметр равен высоте.
6. Эллиптический, гиперболический и параболический. Образованы соответственно эллипсами, гиперболами и параболами.
7. Усеченный. Геометрическое тело, которое отсекается от цилиндра плоскостью, не параллельной основанию.
8. Призма. Является разновидностью цилиндра, если имеет основание в виде многоугольника.

Видео:Цилиндр, конус, шар, 6 классСкачать

Основные формулы для вычисления боковой и полной площади

Кроме рабочих способов, перечисленных выше, рассчитать площадь рассматриваемого тела можно следующими методами:

1. Через диаметр и высоту: \( S_ =D\times\pi\left(h+\frac D2\right); S_ =D\times\pi\times h.\)
2. Через объем: \(S=\frac Vh.\)
3. Через длину окружности. Так как \(l=2\times\pi\times R\) , то \(S_ =l\times h\) , а \(S_ =l\times h+2\times\pi\times R^2\) .

Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Высчитать площадь боковой поверхности цилиндра.

Из этого: \(S_ =2\times3,14\times2\times3=6,28\times6=37,68.\)

\(S_ =24\pi\) , а диаметр основания — 3. Узнать высоту цилиндра.

Видео:Объем цилиндраСкачать

Площадь поверхности цилиндра формула расчета

Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.

Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.

Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Площадь поверхности цилиндра онлайн калькулятор

Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.

Видео:Как запомнить площадь поверхности цилиндра #математикапрофиль #геометрияегэСкачать

Площадь боковой поверхности цилиндра

Сначала нужно представить, как выглядит развертка в двухмерном пространстве.

Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r, где r — радиус окружности. Другая сторона прямоугольника равна высоте h. Найти искомое не составит труда.

Sбок = 2π * r * h,

где число π = 3.14.

Видео:Нахождение площади боковой поверхности цилиндраСкачать

Площадь полной поверхности цилиндра

Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.

Конечная формула выглядит следующим образом:

Sпол = 2π * r2 + 2π * r * h.

Видео:Объем цилиндра.Скачать

Площадь цилиндра формула через диаметр

Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.

Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.

Sпол = 2π * r2 + 2π * r * h = 2π * d2/4 + 2π * h * d/2 = π * d2/2 + π * d * h,

Вместо r в полную формулу нужно вставить значение r = d/2.

Видео:Площадь круга. Математика 6 класс.Скачать

Примеры расчета площади цилиндра

Вооружившись знаниями, приступаем к практике.

Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.

Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:

Sпол = 2 * 3.14 * 242 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм2).

Переводим в привычные м2 и получаем 0,01868928, приблизительно 0.02 м2.

Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.

Данные следующие: диаметр 0,2 м, высота 2 м. Используем формулу через диаметр:

Sпол = 3.14 * 0.22/2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м2.

Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.

Sбок = 2 * 3.14 * 1 * 1 = 6.28 м2.

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Заключение

В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.

Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.

Видео:Площадь поверхности цилиндраСкачать

Как посчитать объем цилиндра

Видео:Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ ( 1 /₂) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см 2 , то:

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см 2 , то:

V = 30 2 / _{4 ⋅ 3.14⋅ 5} = 900 /_62.8 = 14.33 см 3