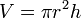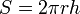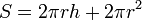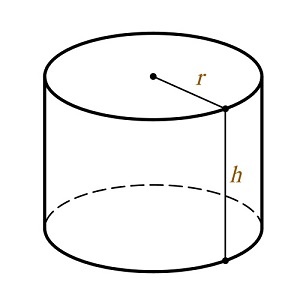
Как выглядит цилиндр по математике

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:Видеоурок по математике "Цилиндр"Скачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

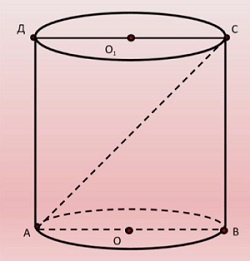
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:Цилиндр, конус, шар, 6 классСкачать

Основные элементы цилиндра

• Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
• R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
• O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
• l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

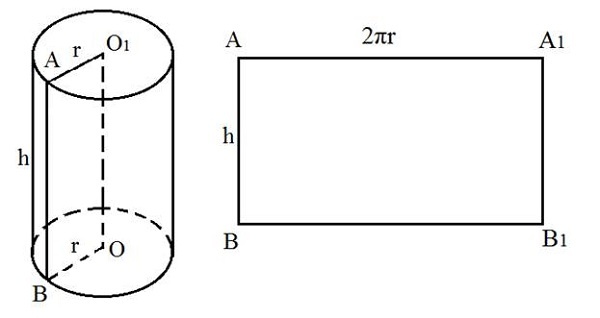
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

• длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
• ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:Объемные Геометрические ФИГУРЫ Загадки для ДЕТЕЙСкачать

Видеоурок по математике «Цилиндр»

План-конспект урока

Образовательные цели: сформировать у учащихся представления о цилиндре и связанных с ним понятий. Научить применять формулы для нахождения объема, площадей боковой и полной поверхностей цилиндра при решении задач.

Развивающие цели: содействовать развитию пространственного мышления. Содействовать развитию умений обобщать и систематизировать полученные знания.

Воспитательные цели: привить интерес к геометрии. Воспитать ответственное отношение к учебному труду.

Тип урока: урок объяснения нового материала.

1. Организационный момент.

─ проверка готовности учащихся к уроку;

─ организация внимания учащихся.

2. Объяснение нового материала.

Итак, рассмотрим понятие цилиндра. Цилиндр — это один из видов тел вращения. Вокруг нас существует множество предметов, имеющих форму цилиндра.

Далее назовем элементы цилиндра и дадим его определение:

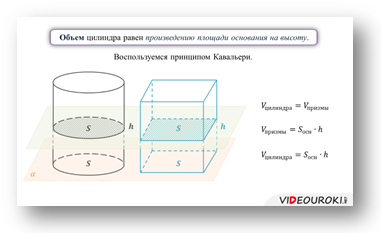
Затем, пользуясь принципом Кавальери, докажем, объем цилиндра равен произведению площади основания на высоту.

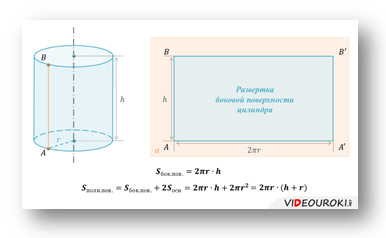
Потом рассмотрим цилиндр с радиусом r и высотой h. Покажем его развертку и выведем формулы для вычисления площадей боковой и полной поверхностей цилиндра.

3. Обобщение и закрепление нового материала.

На этом уроке мы познакомились с понятием цилиндра. Узнали, что цилиндр — это тело, ограниченное двумя равными кругами и цилиндрической поверхностью. Рассмотрели, какими элементами он обладает. А также разобрались, как находят объем, площадь боковой поверхности и площадь полной поверхности цилиндра.

Читайте также: Honda crf 150 цилиндр

Кроме этого решили задачи на применение формул.

4. Рефлексия.

Хотелось бы узнать, понравился ли вам урок? Что было не понятным на уроке? Что еще бы вы хотели узнать?

Видео:Математика 4 класс (Урок№66 - Цилиндр.)Скачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:ЦИЛИНДР. КОНУС. ШАР.Скачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Как выглядит цилиндр по математике

Ц илиндр, получается в результате вращения прямоугольника вокруг одной из его сторон.

• Цилиндр состоит из двух кругов и множества отрезков .
• Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов.
• Определения элементов цилиндра :

Основания цилиндра – равные круги, расположенные в параллельных плоскостях

Высота цилиндра — это расстояние между плоскостями его оснований.

Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра).

Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники

Образующая цилиндра — это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра.

Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра .

Радиус цилиндра – это радиус его основания.

Прямой цилиндр – это цилиндр, образующие которого перпендикулярны основанию.

Равновеликий цилиндр – цилиндр, у которого высота равна диаметру (показать равновеликий цилиндр: кнопкой со значком руки перевести модель обратно в интерактивный режим и изменить значение высоты и радиуса у предложенной модели так, чтобы ).

Вывод формулы площади боковой поверхности.

Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C , где H – высота цилиндра, а C – длина окружности основания. Получим формулы для вычисления площадей боковой S _б и полной S _п поверхностей: S _б = H · C = 2π RH , S _п = S _б + 2 S = 2π R ( R + H ).

Задача № 1. Вычислить площадь боковой и полной поверхности цилиндра, у которого радиус равен 3 см, а высота 5 см (число пи и ответ округлить до целых).

2. Высота цилиндра равна h , радиус основания R . Найти площадь сечения плоскостью, проведенной параллельно оси цилиндра на, расстоянии a от нее.

Домашнее задание: 522, 524, 526.

Р.S/ кому интересно попрбуйте пройти по ссылке и посмотреть электронный ресурс про цилиндр

для начала на странице установите у себя на ПК модуль ОМS и закачайте модуль. На выскочившей таблице кликните воспроизвести. А дальше по порядку просмотрите все странички.
ВСЕМ СПАСИБО.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Цилиндр (математика)

Цили́ндр (греч. kýlindros , валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра); причём если оснований два, то одно получено из другого параллельным переносом вдоль образующей боковой поверхности цилиндра; и основание пересекает каждую образующую боковой поверхности ровно один раз.

Бесконечное тело, ограниченное замкнутой бесконечной цилиндрической поверхностью, называется бесконечным цилиндром, ограниченное замкнутым цилиндрическим лучом и его основанием, называется открытым цилиндром. Основание и образующие цилиндрического луча называют соответственно основанием и образующими открытого цилиндра.

Конечное тело, ограниченное замкнутой конечной цилиндрической поверхностью и двумя выделившими её сечениями, называется конечным цилиндром, или собственно цилиндром. Сечения называются основаниями цилиндра. По определению конечной цилиндрической поверхности, основания цилиндра равны.

Очевидно, образующие боковой поверхности цилиндра — равные по длине (называемой высотой цилиндра) отрезки, лежащие на параллельных прямых, а концами лежащие на основаниях цилиндра. К математическим курьёзам относят определение любой конечной трёхмерной поверхности без самопересечений как цилиндра нулевой высоты (данную поверхность считают одновременно обоими основаниями конечного цилиндра). Основания цилиндра качественно влияют на цилиндр.

Если основания цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости цилиндра перпендикулярны образующей, то цилиндр называется прямым.

В частности, если основание стоящего на плоскости цилиндра — круг, то говорят о круговом (круглом) цилиндре; если эллипс — то эллиптическом.

Объём конечного цилиндра равен интегралу площади основания по образующей. В частности, объём прямого кругового цилиндра равен

,

(где — радиус основания, — высота).

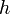
Площадь боковой поверхности цилиндра считается по следующей формуле:

.

Площадь полной поверхности цилиндра складывается из площади боковой поверхности и площади оснований. Для прямого кругового цилиндра:

.

Видео:Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать

Определение цилиндра: его основание и высота, разновидности

Разбираемся в особенностях трехмерного геометрического тела под названием цилиндр. Смотрим виды цилиндров, его свойства, какие бывают развертки, а также даем определения составным частям этой фигуры.

Видео:ЦИЛИНДР // КОНУС // ШАРСкачать

Что такое цилиндр в геометрии

Цилиндр — это трехмерное геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными плоскостями.

Цилиндрическая поверхность — это поверхность, которая образуется за счет движения в пространстве прямой (образующей) параллельно самой себе, пересекающей данную линию (направляющую).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Основания — это одинаковые круги, которые ограничивают цилиндр и находятся параллельно друг другу.

Образующая — отрезок, который соединяет точки окружностей оснований цилиндра и перпендикулярный плоскостям этих оснований. Она равна высоте цилиндра или расстоянию от одного его основания до другого.

Видео:ЦИЛИНДР геометрия егэ по математике профильный уровень ЯщенкоСкачать

Виды цилиндров

Классификация цилиндров может быть разной в зависимости от тех или иных параметров:

• по наклону образующей;
• по форме основания.

У прямого цилиндра образующие строго перпендикулярны основаниям фигуры.

В случае, когда этот угол не равен \(90^\circ\) , цилиндр называют наклонным.

Помимо кругов, в основаниях фигуры могут быть еще и эллипсы или другие замкнутые фигуры. Однако, кроме замкнутых форм, основании цилиндру может служить и парабола, и гипербола, и любая друга открытая функция. Такой цилиндр будет называться развернутым.

Видео:Цилиндр, конус и шар в задании 2 | Математика ЕГЭ 2023 | УмскулСкачать

Как найти высоту цилиндра

Рассмотрим варианты нахождения высоты фигуры, а также длины ее образующей (которая равна этой высоте).

• Первым делом взглянем на формулу: \(V=\pi R^2\times H\) , где V — объем цилиндра, R — радиус основания, H — высота фигуры.

Через эту формулу можем выразить высоту:

Таким образом мы можем узнать H данного геометрического тела, если нам известен его объем и радиус. Если же вместо радиуса мы знаем диаметр, формула расчета будет выглядеть так:

В случае, когда нам известен диаметр и площадь фигуры, мы так же можем найти высоту. Следует обратить внимание, что в зависимости от того, будет ли известна площадь боковой или полной поверхности, формула будет меняться.

Для расчета S боковой поверхности (часть, ограниченная цилиндрической поверхностью) цилиндра мы используем формулу:

Если известна S полной поверхности (включает в себя площадь оснований фигуры), используем формулу:

\(S=2\pi R(H+R)=2\pi R\times H+2\pi R^2\)

• Для третьего способа нужно будет провести прямоугольное сечение, ширина которого должна будет совпадать с диаметрами оснований, а длина — с образующими цилиндра.

Таким образом, получается прямоугольный треугольник САВ. А так как высота равна образующей, мы можем вычислить ее по теореме Пифагора:

Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Развертка

Как уже было упомянуто выше, всего существует две площади поверхности цилиндра: боковой поверхности и полной поверхности. У каждой из них также есть и своя развертка. Разберемся, как они выглядят.

Развертка боковой поверхности

Легче всего представить себе развертку боковой поверхности цилиндра, посмотрев на этикетку пластиковой бутылки. Когда вы ее отклеиваете, то видите прямоугольник. То же самое и с цилиндрическим геометрическим телом: развёрткой его боковой поверхности является прямоугольник. Его длина соответствует длине окружности, лежащей в основании, а ширина — высоте самой трехмерной фигуры.

Развертка полной поверхности

Если развернуть полную поверхность цилиндра, получится примерно то же самое, только с двумя дополнительными элементами в виде окружностей оснований. Выглядит это так:

🔥 Видео

9 класс, 41 урок, ЦилиндрСкачать

6 класс. Цилиндр. МатематикаСкачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

11 класс, 14 урок, Понятие цилиндраСкачать

ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

БИТВА С МАТЕМАТИКОМ ( The Eternal Cylinder )Скачать

Цилиндр - расчёт площади, объёма.Скачать