Для того, что-бы сразу получить готовую развертку цилиндра, кликните по ссылке.
Для получения готовой развертки наклонного цилиндра, кликните по этой ссылке.
Если нужна развертка конуса, то переходите сюда.
Для получения развертки усеченного конуса, переходите сюда..
Если же Вас интересует вопрос, как сделать развертку цилиндра самостоятельно, без использования калькулятора разверток, то следующая статья для Вас.
- Развертка цилиндра для склеивания
- Развертка цилиндра для склеивания шаблон
- Популярное
- Развертка усеченного цилиндра. Построение развертки цилиндра.
- Развертка усеченного цилиндра. Построение развертки цилиндра.
- Развертка верхней части цилиндра.
- Построение сечения цилиндра.
- Развертка наклонного усеченного цилиндра. Наклонный цилиндр развертка.
- Наклонный цилиндр развертка.
- Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
- Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
- Развертка прямого кругового цилиндра.
- Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
- Развертка усеченного цилиндра.
- 📹 Видео
Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать
Развертка цилиндра для склеивания
Цилиндр — простая геометрическая фигура, представляющая из себя вытянутое тело, ограниченное с обоих сторон двумя плоскостями (основаниями).
Для простоты представления, прямая труба — это цилиндр.
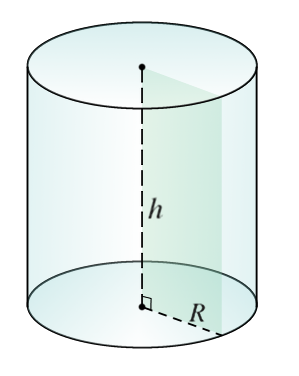
На рисунке 1 изображен прямой круговой цилиндр. Прямой — означает, что угол между осью цилиндра и плоскостью основания — прямой (равен 90 град.), круговой — означает, что в основании цилиндра лежит круг.
Для построения развертки прямого кругового цилиндра потребуются две величины: 1) высота цилиндра (H), 2) диаметр круга, который лежит в основании (D),
Цилиндр может быть не круговым. Например на рисунке 2 изображен овальный цилиндр. Овальный — означает, что в основании цилиндра лежит овал.
Также, цилиндр может быть не прямым, а наклонным. У наклонного цилиндра (меньше 90 град.). На рисунке 3 изображен наклонный цилиндр.
Для построения развертки наклонного цилиндра потребуются три размера: 1) высота цилиндра (H), 2) радиус окружности (R), 3) угол наклона оси (A), Перейти к построению.
Видео:Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать
Развертка цилиндра для склеивания шаблон
Популярное
Сюжет фантастического блокбастера «Пятый элемент», построен на легенде, что существуют пять элементов, которые способны защитить мир от угрозы Абсолютного Зла.
Как вы думаете, что общего у додекаэдра и календаря?
Для первобытного человека когда-то костер стал новой формой общественной жизни. Ночь перестала быть неотвратимым черным провалом и ценность огня заставила.
Какое из известных нам геометрических тел обладает наибольшей прочностью? Наиболее устойчиво к внешним деформациям?
Полуправильные многогранники — это несколько групп многогранников: 1. Архимедовы тела; 2.
Это небольшая «шуточная» задача поможет Вам на некоторое время занять ваших детей! Какой пластиковый тетраэдр* нужно расплавить, чтобы из.
Когда мы готовили 36-ой выпуск «Волшебные грани», у наших коллег возник вопрос: «Почему мы опять собираемся говорить о правильных многогранниках.
Читайте также: Как удалить цилиндр из замка если нет ключа
Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать
Развертка усеченного цилиндра. Построение развертки цилиндра.
Видео:Усеченный конус. 11 класс.Скачать
Развертка усеченного цилиндра. Построение развертки цилиндра.
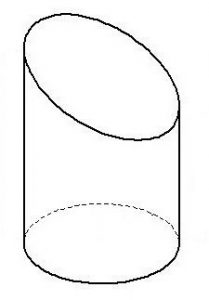
Проекция цилиндра, срезанного плоскостью, наклонной к плоскости чертежа, по вертикальной плоскости проекции дает прямую линию, на горизонтальной — окружность, на профильной плоскости — замкнутую кривую, эллипс в искаженном виде.
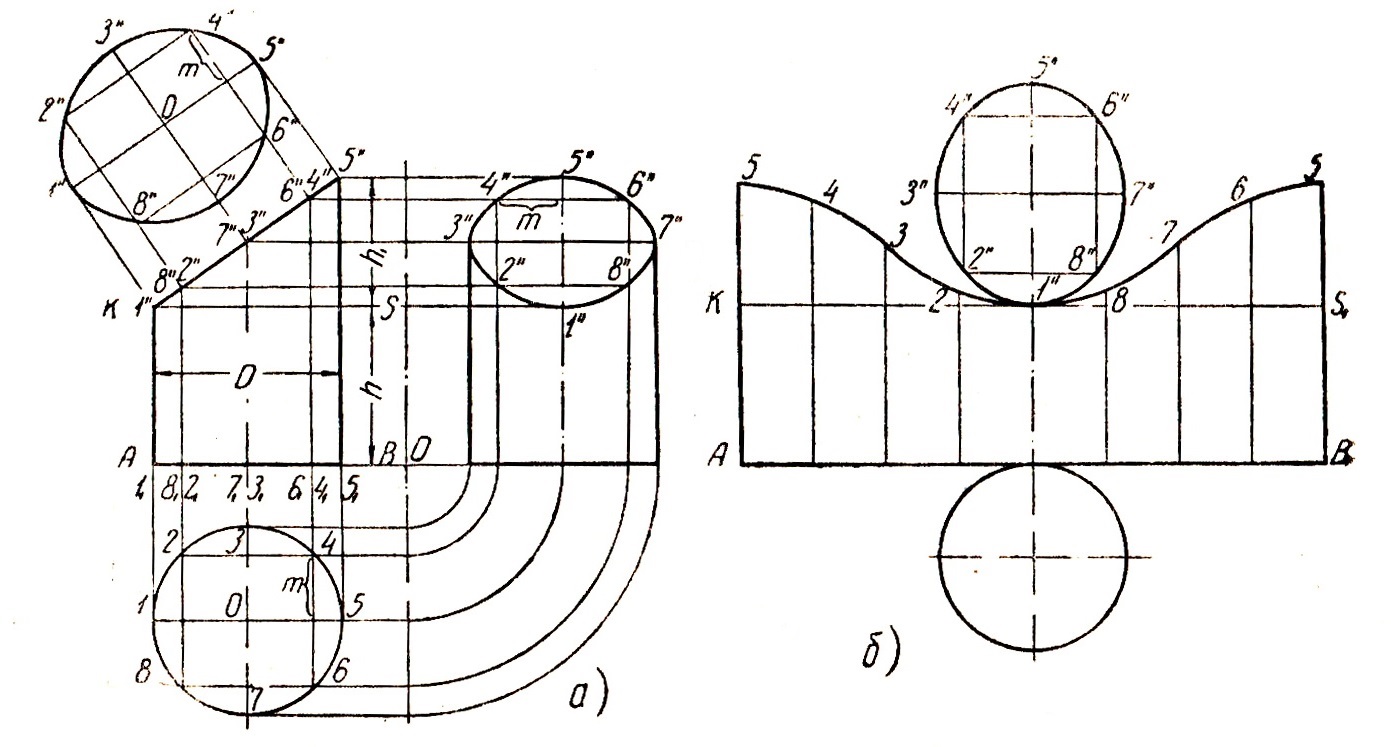
Если представить себе цилиндр, срезанный плоскостью KS (рис. 1, а), параллельной основанию и проходящей через низшую точку наклонного среза 1, то нижняя часть такого цилиндра развернется в прямоугольник A1K1S1B1 (рис. 1, б) с высотой h = BS и основанием А1В1 = πD.
Рис. 1. Развертка усеченного цилиндра:
а — проекция; б — развертка.
Развертка верхней части цилиндра.
Чтобы получить развертку верхней части цилиндра выше плоскости KS, поступают следующим образом. Окружность основания делится на несколько равных частей, в приведенном примере на- восемь равных частей. Точки делений проектируют на вертикальную проекцию и проводят соответствующие образующие цилиндра 11 — 1′; 21 — 2″ и т. д. Затем делят длину развернутой окружности основания на такое же число равных частей, и из точек делений восстанавливают перпендикуляры, которые будут представлять собой те же образующие цилиндра, на которых затем нужно отложить их длины, измеряя одноименные отрезки на вертикальных проекциях (рис. 1, б). Соединив плавной кривой полученные точки, будем иметь развертку боковой поверхности усеченного цилиндра.
Для определения действительной формы поперечного сечения наклонной поверхности цилиндра вводят дополнительную плоскость проекции, параллельную плоскости сечения, на которой форма сечения спроектируется в искаженном виде — в форме эллипса.
Построение сечения цилиндра.
Для построения сечения на дополнительной плоскости проведем линию, параллельную проекции плоскости сечения, и, спроектировав на нее точки 1″ и 5″ с вертикальной проекции, получим большую ось эллипса. Затем из точки 7″ — 3″ на вертикальной проекции проведем линию, перпендикулярную большой оси эллипса, и, отложив на ней вправо и влево от большой оси отрезки 03″ и 07″, равные радиусу основания цилиндра, получим малую ось эллипса 3″ — 7″.
Положение остальных точек 2″, 4″, 6″, 8″ определяется так: на перпендикулярах к большей оси, проведенных из точек 8″ — 2″ и 6″ — 4″ вертикальной проекции, откладываем отрезки m от большей оси эллипса. Плавная кривая, проведенная через полученные восемь точек, будет эллипсом.
Построение эллипса на профильной проекции видно из рис. 1, а.
Для получения полной развертки поверхности цилиндра следует добавить поверхности наклонного сечения и нижнего основания цилиндра, как указано на рис. 1, б.
Видео:Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать
Развертка наклонного усеченного цилиндра. Наклонный цилиндр развертка.
Видео:Развертка усеченного цилиндраСкачать
Наклонный цилиндр развертка.
Возьмем вертикальную и горизонтальную проекции наклонного усеченного цилиндра (рис. 1, а), причем нижнее основание цилиндра проектируется на горизонтальную проекцию без искажения, а верхнее основание проектируется также на горизонтальную проекцию в искаженном виде. Действительная форма верхнего основания проектируется на дополнительную плоскость проекции.
Читайте также: Как рассчитать объем кубов в цилиндре
Развертку наклонного усеченного цилиндра (рис. 1, б) получают аналогично развертке усеченного цилиндра. Плоскостью, перпендикулярной к образующим, цилиндр делят по линии mn на два усеченных цилиндра.
Рис 1. Развертка наклонного усеченного цилиндра:
а — проекция; в — развертка.
На линии mn строится истинное сечение цилиндра, которое будет окружностью. Окружность делится на равное число частей на пример, на восемь частей. Через полученные точки деления окружности проводят образующие цилиндра. Дальнейшее построение истинных очертаний срезанных поверхностей наклонного цилиндра и их проекций видно из рис. 1, б. Каждый полученный цилиндр развертывают в плоскость так, как показано в ст. Развертка усеченного цилиндра, и получают развертку поверхности каждого цилиндра. Сумма обеих разверток с добавлением верхнего и нижнего оснований цилиндра образует полную развертку.
Видео:Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Видео:Рисуем усеченный цилиндр.Скачать
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Развертка прямого кругового цилиндра.
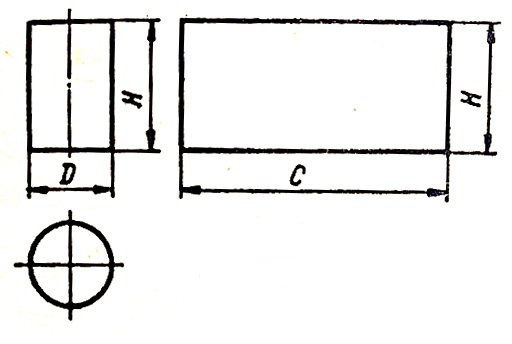
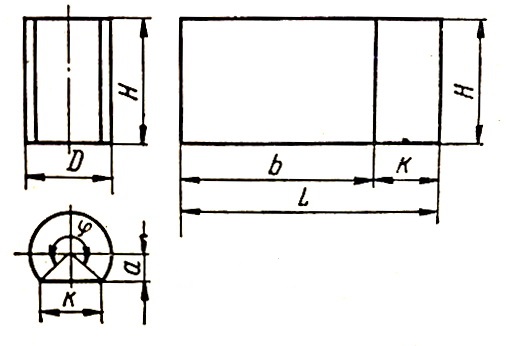
Цилиндр диаметром D и высотой H показан на рис. 1. Развертка представляет собой прямоугольник длиной с = πD и высотой Н.
Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2) 2 – a 2 ) = 2a tg (ᵠ/2).
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
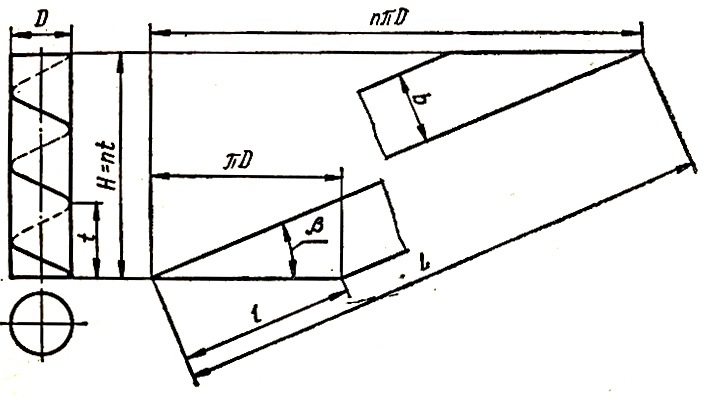
Цилиндр показан на рис. 3. При определении развертки можно использовать следующие зависимости:
n — число полных витков на общей длине цилиндра H, Н = nt;
Развертка усеченного цилиндра.
Для получения развертки горизонтальная проекция цилиндра делится на равные части и точки деления нумеруются (в данном случае от 0 до 12). Из точек деления проводятся вертикали до пересечения верхнего основания в точках 0′1, 1′1…, 6′1. На продолжении прямой 0’6′ откладывается отрезок длиной с = πD, который делится на принятое число равных частей. Из точек деления 00, 10, …, 60 строятся перпендикуляры до их пересечения с соответствующими горизонтальными линиями в точках 0 0 1, 1 0 1, …, 6 0 1. Полученные точки соединяются плавной кривой. Ввиду симметричности остальные точки кривой находит аналогичным путем.
Линию развертки можно определить и таким способом. На расстоянии h1 = (h + H)/2 от линии 0 0 12 0 проводится параллельная прямая. Из центра S, лежащего на прямой, описывается полуокружность радиусом А. Полуокружность делится на равные части, число которых равно половине точек деления развертки (в данном случае на шесть). Через точки деления 0ꞋꞋ, 1ꞋꞋ, …, 6ꞋꞋ проводятся горизонтальные прямые до пересечения вертикалей, проходящих через 0 0 , 1 0 , … , 12 0 . Полученные точки 0 0 1, 1 0 1, …, 12 0 1 соединяются плавной кривой.
Читайте также: Вес блока цилиндров приора
Верхнее основание цилиндра представляет собой эллипс с полуосями a = D/2 cos α = 0′13′1 и b = D/2.
При аналитическом определении координат точек кривой развертки цилиндра, усеченного плоскостью под углом α (рис. 5), могут быть использованы следующие зависимости:
xk = kx1 = πD/2 kε/180°; yk = D/2 tg α sin kε = A sin kε = A sin ᵠi,
где х1 = πD/ (2n) = πD/2 ε/180° — длина дуги окружности основания цилиндра, разделенная на 2n равных частей; ε = 360°/2n — центральный угол, соответствующий одному делению; k — порядковый номер точки; A = (H — h)/2 = (D/2) tg α — амплитуда синусоиды; ᵠi= kε.
Значения sin kε для наиболее часто употребляемых значений 2n приведены в табл. 1.
Таблица 1. Значения sin kε и sin 2 kε
| 2n | sin kε | sin 2 kε | 2n | sin kε | sin 2 kε | ||||||
| 8 | 16 | 32 | 64 | 12 | 24 | 48 | 96 | ||||
| — | — | — | 1 | 0,09802 | 0,00961 | — | — | — | 1 | 0,06540 | 0,00428 |
| — | — | 1 | 2 | 0,19509 | 0,03806 | — | — | 1 | 2 | 0,13053 | 0,01704 |
| — | — | — | 3 | 0,29028 | 0,08426 | — | — | — | 3 | 0,19509 | 0,03806 |
| — | 1 | 2 | 4 | 0,38268 | 0,14645 | — | 1 | 2 | 4 | 0,25882 | 0,06699 |
| — | — | — | 5 | 0,47139 | 0,22221 | — | — | — | 5 | 0,32144 | 0,10332 |
| — | — | 3 | 6 | 0,55557 | 0,30866 | — | — | 3 | 6 | 0,38268 | 0,14645 |
| — | — | — | 7 | 0,63439 | 0,40245 | — | — | — | 7 | 0,44229 | 0,19562 |
| 1 | 2 | 4 | 8 | 0,70711 | 0,50000 | 1 | 2 | 4 | 8 | 0,50000 | 0,25000 |
| — | — | — | 9 | 0,77301 | 0,59754 | — | — | — | 9 | 0,55557 | 0,30866 |
| — | — | 5 | 10 | 0,83147 | 0,69134 | — | — | 5 | 10 | 0,60876 | 0,37059 |
| — | — | — | 11 | 0,88192 | 0,77778 | — | — | — | 11 | 0,65935 | 0,43474 |
| — | 3 | 6 | 12 | 0,92388 | 0,85355 | — | 3 | 6 | 12 | 0,70711 | 0,50000 |
| — | — | — | 13 | 0,95694 | 0,91573 | — | — | — | 13 | 0,75184 | 0,56526 |
| — | — | 7 | 14 | 0,98079 | 0,96194 | — | — | 7 | 14 | 0,79335 | 0,62941 |
| — | — | — | 15 | 0,99518 | 0,99039 | — | — | — | 15 | 0,83147 | 0,69134 |
| 2 | 4 | 8 | 16 | 1,00000 | 1,00000 | 2 | 4 | 8 | 16 | 0,86617 | 0,75000 |
| — | — | — | 17 | 0,89687 | 0,80438 | ||||||
| — | — | 9 | 18 | 0,92388 | 0,85355 | ||||||
| — | — | — | 19 | 0,94693 | 0,89668 | ||||||
| — | 5 | 10 | 20 | 0,96600 | 0,93301 | ||||||
| — | — | — | 21 | 0,98079 | 0,96194 | ||||||
| — | — | 11 | 22 | 0,99144 | 0,98296 | ||||||
| — | — | — | 23 | 0,99786 | 0,99572 | ||||||
| 3 | 6 | 12 | 24 | 1,00000 | 1,00000 | ||||||
Примечание: Значения sin kε и sin 2 kε даны для одной четверти окружности. В остальных четвертях они повторяются.
Ввиду симметричности синусоиды достаточно определить координаты точек одной четверти окружности, например от у0 до у3. Остальные координаты имеют соответственно равные значения. Например: у4 — у2, …, у11 = — у1 и т. д.
📹 Видео
Часть 1 Усечённый цилиндрСкачать
Часть 2 Усечённый цилиндрСкачать
Построение развёртки усечённого цилиндра.Скачать
Построение усеченного цилиндра с сечением в натуральную величинуСкачать
Простой расчёт развёртки конусаСкачать
Расчет развертки усеченного цилиндра в Компас 3Д. Чертеж развертки усеченного цилиндра.Скачать
Построение изометрии усеченного цилиндра │Урок #60Скачать
Цилиндр. Усеченный конус (прямой)Скачать
Хон или зеркало? Научно-практический коментарийСкачать
Лекция #13Скачать
Как легко сделать усеченный конус (конус) из металла 2 мм. Сделай сам!Скачать
