Как выполнить развертку цилиндра (7 видео)

Для того, что-бы сразу получить готовую развертку цилиндра, кликните по ссылке.
Для получения готовой развертки наклонного цилиндра, кликните по этой ссылке.
Если нужна развертка конуса, то переходите сюда.
Для получения развертки усеченного конуса, переходите сюда..

Если же Вас интересует вопрос, как сделать развертку цилиндра самостоятельно, без использования калькулятора разверток, то следующая статья для Вас.

Содержание

Развертка цилиндра для склеивания
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.
Развертка прямого кругового цилиндра.
Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.
Развертка усеченного цилиндра.
📺 Видео

Видео:Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать

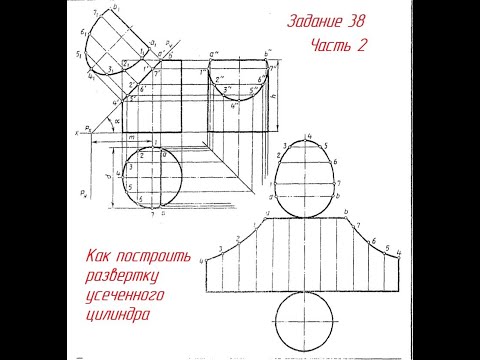
Развертка цилиндра для склеивания

Цилиндр — простая геометрическая фигура, представляющая из себя вытянутое тело, ограниченное с обоих сторон двумя плоскостями (основаниями).
Для простоты представления, прямая труба — это цилиндр.
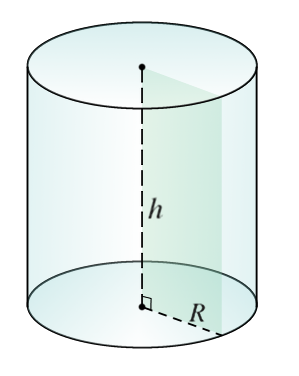
На рисунке 1 изображен прямой круговой цилиндр. Прямой — означает, что угол между осью цилиндра и плоскостью основания — прямой (равен 90 град.), круговой — означает, что в основании цилиндра лежит круг.

Для построения развертки прямого кругового цилиндра потребуются две величины: 1) высота цилиндра (H), 2) диаметр круга, который лежит в основании (D),

Цилиндр может быть не круговым. Например на рисунке 2 изображен овальный цилиндр. Овальный — означает, что в основании цилиндра лежит овал.

Также, цилиндр может быть не прямым, а наклонным. У наклонного цилиндра (меньше 90 град.). На рисунке 3 изображен наклонный цилиндр.

Для построения развертки наклонного цилиндра потребуются три размера: 1) высота цилиндра (H), 2) радиус окружности (R), 3) угол наклона оси (A), Перейти к построению.

Видео:Построение развертки цилиндра. Урок 37.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.

Видео:Как сделать ИДЕАЛЬНЫЙ цилиндр из бумагиСкачать

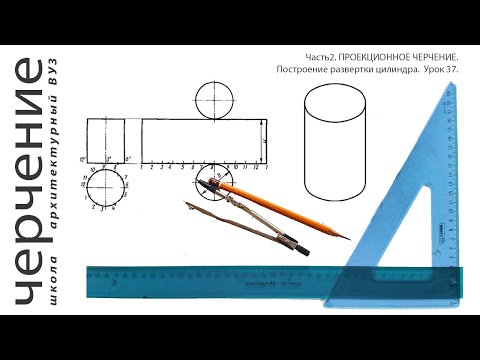
Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.

Развертка прямого кругового цилиндра.

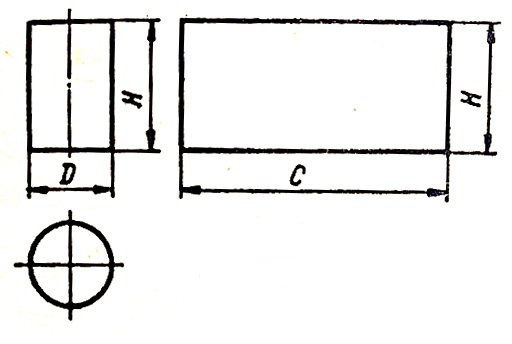
Цилиндр диаметром D и высотой H показан на рис. 1. Развертка представляет собой прямоугольник длиной с = πD и высотой Н.

Читайте также: Двигатель алтай рядный 6 цилиндров

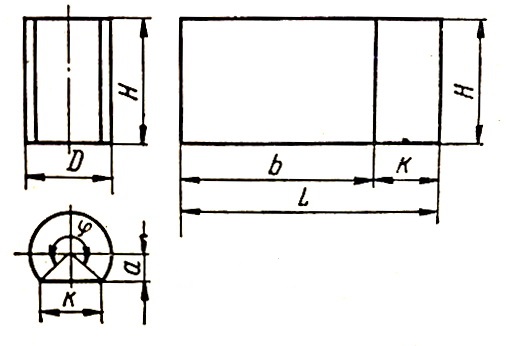
Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2) 2 – a 2 ) = 2a tg (ᵠ/2).

Развертка прямого кругового цилиндра из ленты. Расчет развертки цилиндра.

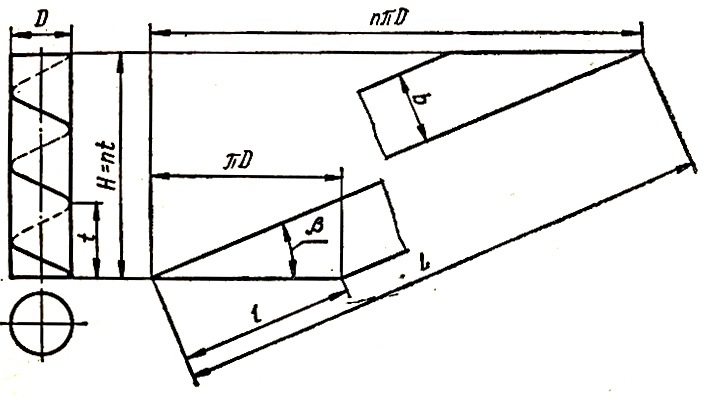
Цилиндр показан на рис. 3. При определении развертки можно использовать следующие зависимости:

n — число полных витков на общей длине цилиндра H, Н = nt;

Развертка усеченного цилиндра.

Для получения развертки горизонтальная проекция цилиндра делится на равные части и точки деления нумеруются (в данном случае от 0 до 12). Из точек деления проводятся вертикали до пересечения верхнего основания в точках 0′₁, 1′₁…, 6′₁. На продолжении прямой 0’6′ откладывается отрезок длиной с = πD, который делится на принятое число равных частей. Из точек деления 0₀, 1₀, …, 6₀ строятся перпендикуляры до их пересечения с соответствующими горизонтальными линиями в точках 0 0 ₁, 1 0 ₁, …, 6 0 ₁. Полученные точки соединяются плавной кривой. Ввиду симметричности остальные точки кривой находит аналогичным путем.

Линию развертки можно определить и таким способом. На расстоянии h1 = (h + H)/2 от линии 0 0 12 0 проводится параллельная прямая. Из центра S, лежащего на прямой, описывается полуокружность радиусом А. Полуокружность делится на равные части, число которых равно половине точек деления развертки (в данном случае на шесть). Через точки деления 0ꞋꞋ, 1ꞋꞋ, …, 6ꞋꞋ проводятся горизонтальные прямые до пересечения вертикалей, проходящих через 0 0 , 1 0 , … , 12 0 . Полученные точки 0 0 ₁, 1 0 ₁, …, 12 0 ₁ соединяются плавной кривой.

Верхнее основание цилиндра представляет собой эллипс с полуосями a = D/2 cos α = 0′₁3′₁ и b = D/2.

При аналитическом определении координат точек кривой развертки цилиндра, усеченного плоскостью под углом α (рис. 5), могут быть использованы следующие зависимости:

x_k = kx₁ = πD/2 kε/180°; y_k = D/2 tg α sin kε = A sin kε = A sin ᵠ_i,

Читайте также: Присадка для восстановления цилиндров xado revitalizant ex120 туба 9 мл

где х₁ = πD/ (2n) = πD/2 ε/180° — длина дуги окружности основания цилиндра, разделенная на 2n равных частей; ε = 360°/2n — центральный угол, соответствующий одному делению; k — порядковый номер точки; A = (H — h)/2 = (D/2) tg α — амплитуда синусоиды; ᵠ_i= kε.

Значения sin kε для наиболее часто употребляемых значений 2n приведены в табл. 1.

Таблица 1. Значения sin kε и sin 2 kε

2n				sin kε	sin 2 kε	2n				sin kε	sin 2 kε
8	16	32	64	sin kε	sin 2 kε	12	24	48	96	sin kε	sin 2 kε
—	—	—	1	0,09802	0,00961	—	—	—	1	0,06540	0,00428
—	—	1	2	0,19509	0,03806	—	—	1	2	0,13053	0,01704
—	—	—	3	0,29028	0,08426	—	—	—	3	0,19509	0,03806
—	1	2	4	0,38268	0,14645	—	1	2	4	0,25882	0,06699
—	—	—	5	0,47139	0,22221	—	—	—	5	0,32144	0,10332
—	—	3	6	0,55557	0,30866	—	—	3	6	0,38268	0,14645
—	—	—	7	0,63439	0,40245	—	—	—	7	0,44229	0,19562
1	2	4	8	0,70711	0,50000	1	2	4	8	0,50000	0,25000
—	—	—	9	0,77301	0,59754	—	—	—	9	0,55557	0,30866
—	—	5	10	0,83147	0,69134	—	—	5	10	0,60876	0,37059
—	—	—	11	0,88192	0,77778	—	—	—	11	0,65935	0,43474
—	3	6	12	0,92388	0,85355	—	3	6	12	0,70711	0,50000
—	—	—	13	0,95694	0,91573	—	—	—	13	0,75184	0,56526
—	—	7	14	0,98079	0,96194	—	—	7	14	0,79335	0,62941
—	—	—	15	0,99518	0,99039	—	—	—	15	0,83147	0,69134
2	4	8	16	1,00000	1,00000	2	4	8	16	0,86617	0,75000
—	—	—	17	0,89687	0,80438
—	—	9	18	0,92388	0,85355
—	—	—	19	0,94693	0,89668
—	5	10	20	0,96600	0,93301
—	—	—	21	0,98079	0,96194
—	—	11	22	0,99144	0,98296
—	—	—	23	0,99786	0,99572
3	6	12	24	1,00000	1,00000

Читайте также: Корпус для замка под цилиндр

Примечание: Значения sin kε и sin 2 kε даны для одной четверти окружности. В остальных четвертях они повторяются.

Ввиду симметричности синусоиды достаточно определить координаты точек одной четверти окружности, например от у₀ до у₃. Остальные координаты имеют соответственно равные значения. Например: у₄ — у₂, …, у₁₁ = — у₁ и т. д.